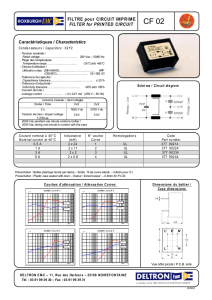
Circuit R L

GBF
R
Input B
Input A
i
A
M
B
A. Loi d’Ohm pour une bobine : étude expérimentale
1) Montage :
Le GBF est à masse flottante (non reliée à la Terre) afin de séparer les
masses du GBF et de l’interface et éviter ainsi de court-circuiter la
bobine.
Le GBF délivre une tension en dents de scie.
R = 10 k
La résistance de la bobine est négligeable.
2) Questions :
 Placer sur le schéma les flèches tension uAM et uMB.
 A quelle tension correspond UA1 au niveau de l’interface ? UA1 correspond à la tension uAM
 Pourquoi cette tension permet-elle de visualiser le courant i du circuit ?
Aux bornes de la résistance : uAM = + R i
 Quelle est l’expression de i en fonction de uAM
AM
1
iu
R
 A quelle tension correspond UB1 au niveau de l’interface ? UB1 correspond à uBM = (- uMB)
 Comment peut-on visualiser la tension uMB ? uMB = - UB1
3) Etude pour f = 333 Hz
On règle la fréquence du GBF à f = 333 Hz et les paramètres de CASSY :
 Sur la ½ période (0<t<T/2), quelle est la forme de la tension uAM ? c’est une fonction affine croissante (
coefficient directeur positif)
 Sur la ½ période (0<t<T/2), quelle est la forme de la tension uMB ? c’est une fonction constante positive : uMB= +
0,14 V
 Même question sur la ½ période T/2<t<T).
quelle est la forme de la tension uAM ? c’est une fonction affine décroissante ( coefficient directeur négatif)
Sur la ½ période (0<t<T/2), quelle est la forme de la tension uMB ? c’est une fonction constante négative : uMB= -
0,14 V
GBF
R
Input B
Input A
i
A
M
B
uAM
uMB

 Sur la ½ période :0<t<T/2 :
 Calculer
3
AM AM
du u ( 1,5) ( 1) 2,8.10 V/s
dt t (2,9) (2,0)
 en déduire
31
AM 4
di 1 du 1 2,8.10 2,8.10 A/s
dt R dt 10 
 Comparer uMB et
dt
di
, c’est à dire, calculer :
dt
di
MBu
MB 1
u 0,14 0,50S.I
di 2,8.10
dt
UAM
UMB
T/2
0

4) Inductance d’une bobine :
On fait varier la fréquence du GBF.
Pour la courbe f = 667 Hz :
 Sur la ½ période :0<t<T/2 :
 Calculer
3
AM 3
du 1,5 ( 1,3) 5,6.10 V/s
dt (1,8 1,3).10
;
 en déduire
31
4
di 1 5,6.10 5,6.10 A/s
dt 10 
 Comparer uMB et
dt
di
( c’est à dire, calculer :
dt
di
MBu
MB 1
u 0,3 0,54S.I
di 5,6.10
dt
f = 667 Hz
0

Pour la courbe f = 1000 Hz :
 Sur la ½ période :0<t<T/2 :
 Calculer
3
AM 3
du 1,5 ( 1,8) 8,2.10 V/s
dt (1,2 0,8).10
;
 en déduire
31
4
di 1 8,2.10 8,2.10 A/s
dt 10 
 Comparer uMB et
dt
di
( c’est à dire, calculer :
dt
di
MBu
MB 3
u 0,45 0,55S.I
di 8,2.10
dt
f = 1000 Hz

Compléter le tableau suivant pour 0<t<T/2 :
f (Hz)
333
667
1000
dt
du
R
1
dt
di AB
(A.s-1)
2,8.10-1
5,6.10-1
8,2.10-1
uMB (V)
0,14
0,3
0,45
uMB /
dt
di
0,50
0,54
0,55
Que déduit-on de la dernière ligne du tableau? Conclure.
Aux erreurs expérimentales ( et de lecture !) près, on voit que le rapport (uMB /
dt
di
) est constant ;
On l’appelle « inductance de la bobine » ; il ne dépend que de la géométrie de la bobine