1. Nature des rayons X - Lycée Gustave Flaubert Rouen
publicité
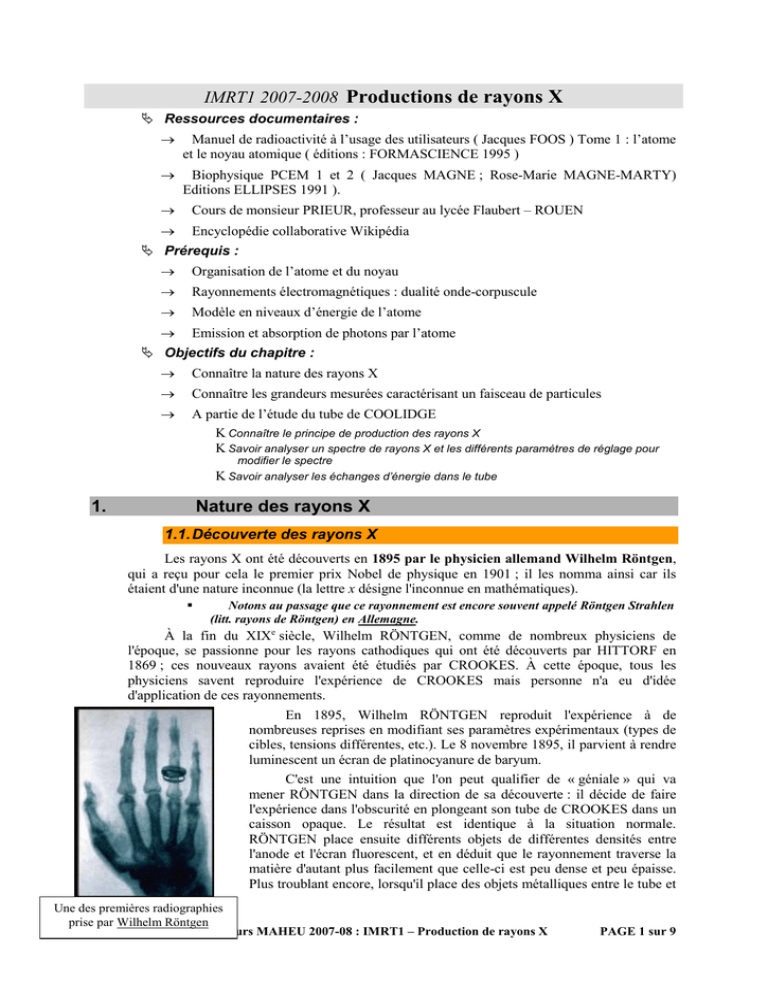
IMRT1 2007-2008 Productions de rayons X Ressources documentaires : Manuel de radioactivité à l’usage des utilisateurs ( Jacques FOOS ) Tome 1 : l’atome et le noyau atomique ( éditions : FORMASCIENCE 1995 ) Biophysique PCEM 1 et 2 ( Jacques MAGNE ; Rose-Marie MAGNE-MARTY) Editions ELLIPSES 1991 ). Cours de monsieur PRIEUR, professeur au lycée Flaubert – ROUEN Encyclopédie collaborative Wikipédia Prérequis : Organisation de l’atome et du noyau Rayonnements électromagnétiques : dualité onde-corpuscule Modèle en niveaux d’énergie de l’atome Emission et absorption de photons par l’atome Objectifs du chapitre : Connaître la nature des rayons X Connaître les grandeurs mesurées caractérisant un faisceau de particules A partie de l’étude du tube de COOLIDGE Connaître le principe de production des rayons X Savoir analyser un spectre de rayons X et les différents paramètres de réglage pour modifier le spectre Savoir analyser les échanges d’énergie dans le tube 1. Nature des rayons X 1.1. Découverte des rayons X Les rayons X ont été découverts en 1895 par le physicien allemand Wilhelm Röntgen, qui a reçu pour cela le premier prix Nobel de physique en 1901 ; il les nomma ainsi car ils étaient d'une nature inconnue (la lettre x désigne l'inconnue en mathématiques). Notons au passage que ce rayonnement est encore souvent appelé Röntgen Strahlen (litt. rayons de Röntgen) en Allemagne. À la fin du XIXe siècle, Wilhelm RÖNTGEN, comme de nombreux physiciens de l'époque, se passionne pour les rayons cathodiques qui ont été découverts par HITTORF en 1869 ; ces nouveaux rayons avaient été étudiés par CROOKES. À cette époque, tous les physiciens savent reproduire l'expérience de CROOKES mais personne n'a eu d'idée d'application de ces rayonnements. En 1895, Wilhelm RÖNTGEN reproduit l'expérience à de nombreuses reprises en modifiant ses paramètres expérimentaux (types de cibles, tensions différentes, etc.). Le 8 novembre 1895, il parvient à rendre luminescent un écran de platinocyanure de baryum. C'est une intuition que l'on peut qualifier de « géniale » qui va mener RÖNTGEN dans la direction de sa découverte : il décide de faire l'expérience dans l'obscurité en plongeant son tube de CROOKES dans un caisson opaque. Le résultat est identique à la situation normale. RÖNTGEN place ensuite différents objets de différentes densités entre l'anode et l'écran fluorescent, et en déduit que le rayonnement traverse la matière d'autant plus facilement que celle-ci est peu dense et peu épaisse. Plus troublant encore, lorsqu'il place des objets métalliques entre le tube et Une des premières radiographies prise par Wilhelm Röntgen Cours MAHEU 2007-08 : IMRT1 – Production de rayons X PAGE 1 sur 9 une plaque photographique, il parvient à visualiser l'ombre de l'objet sur le négatif. RÖNTGEN parvient à en déduire que les rayons sont produits dans la direction des électrons du tube et que ce rayonnement est invisible et très pénétrant. 1.2. Aspect ondulatoire des rayons X Compris entre les UV et les rayons gamma, les rayons X sont des ondes électromagnétiques de courtes longueur d’onde comprises sensiblement entre 5 pm et 10 nm . Leurs fréquences sont par conséquent très élevées. Calcul du domaine de fréquence correspondant Remarque : Un aspect particulier de leur caractère ondulatoire est très utilisé en cristallographie. En effet, leur diffraction sur des réseaux cristallins produit des figures de diffraction caractéristiques qui permettent de déterminer la géométrie du réseau. Cependant, l’aspect qui donne lieu aux applications médicales ( radiologie, radiothérapie ) est leur aspect corpusculaire. 1.3. Aspect corpusculaire des rayons X Les photons X sont des corpuscules de masse nulle et d’énergie E h h. C . Leur énergie est importante et de l’ordre de quelques keV à quelques centaines de keV. Calcul du domaine d’énergie correspondant Comme ROENTGEN l’avait observé , il s’agit donc de rayonnements très énergétiques donc très pénétrants. Plus leur longueur d’onde est courte, plus ils sont énergétiques et donc pénétrants. 1.4. Grandeurs caractérisant un rayonnement ou un faisceau électromagnétique 1.4.a. Définitions N : Flux particulaire : ( ou débit ) : nombre de photons par unité de temps N n (unité : s-1 ) t P : Flux énergétique : ( ou puissance ) : énergie par unité de temps P E (unité : J.s-1 ou Watt ( W ) ) ou E P.t . t 1.4.b. Faisceau monochromatique ( ou monoénergétique ) C’est le cas d’un rayonnement fournissant des photons de même fréquence ( ou de même longueur d’onde C ) transportant chacun la même énergie E h . Pendant une durée t, n photons ont été émis, chacun transportant une énergie E h . On en déduit donc l’énergie totale transportée pendant la durée t, qui est égale à n.E . On obtient finalement la puissance transportée par ce rayonnement P Etotale n.E n .E N .E . On a donc P N.E N.h. t t t 1.4.c. Faisceau polyénergétique ou polychromatique C’est le cas d’un rayonnement fournissant des photons de fréquences différentes 1 , 2 , 3 …. ( ou de longueurs d’onde 1 , 2 , 3 …) transportant des énergies E1 , E2 , E3 ….avec des flux particulaires différents N1 , N 2 , N 3 …. Cours MAHEU 2007-08 : IMRT1 – Production de rayons X PAGE 2 sur 9 Le flux particulaire ( ou débit de photons ) total est alors : N N1 N 2 N3 ... Le flux énergétique ( ou puissance rayonnée P P1 P2 P3 .... soit P N1.E1 N2 .E2 N3.E3 .... ) total est alors : Remarque : il est dans ce cas possible de définir l’énergie moyenne du rayonnement par P N .Emoy soit Emoy P P P .... P 1 2 3 N N1 N 2 N3 ... 1.4.d. Intensité énergétique L’intensité énergétique I d’un rayonnement est la puissance qui traverse une unité de surface ( soit une surface de 1 m2 ); on la définit donc par I P S P ( en W ) est la puissance du rayonnement traversant une surface S ( en m2 ) L’intensité énergétique I s’exprime donc en W.m-2 . A. Faisceau parallèle C’est le cas de faisceaux bien focalisés. Le section S du faisceau est constante, de même que le nombre de photons émis par seconde . S S Par conséquent, l’intensité énergétique du faisceau I P est constante tout le long du S faisceau . Exercice 1-3 B. Faisceau sphérique C’est le cas de faisceaux émis par une source ponctuelle M dans toutes les directions de l’espace avec une même célérité ; dans ce cas le front d’onde est une sphère. En effet : d = MA = MB C A P A l’instant t = 0, les photons sont émis par la source M A un instant t > 0, les photons ont tous parcouru la même distance d = C.t et vont traverser une sphère de rayon d et de surface S 4 .d 2 centrée sur M. B On en déduit l’intensité énergétique du faisceau I P P . Celle-ci diminue fortement avec la S 4 .d 2 distance, puisqu’elle diminue avec l’inverse du carré de la distance d . Si d est doublée, I est divisée par 4 Si d est décuplée, I est divisée par 100 Exercices 1-1, 1-2 Cours MAHEU 2007-08 : IMRT1 – Production de rayons X PAGE 3 sur 9 2. Production de R.X Cathode C Rhéostat A générateur basse tension UAC générateur haute tension Historiquement, le premier tube à rayons X fut inventé par sir William Crookes. Il s'agissait à l'origine de provoquer une fluorescence lumineuse de minéraux. Le tube de CROOKES est encore appelé tube à décharge, tube à gaz ou tube à cathode froide. Le tube de CROOKES fut amélioré par William Coolidge en 1913. Le tube de COOLIDGE, encore appelé tube à cathode chaude, est le tube le plus largement utilisé. C'est un tube sous vide poussé (env. 10-4 Pa ), recouvert d'une enceinte plombée. La cathode portée à haute température du fait du chauffage du filament émet (par effet thermoélectronique) des électrons formant un nuage autour d’elle. dans certains tubes, une pièce de forme particulière ayant une tension légèrement négative par rapport au filament (c'est-à-dire par rapport aux deux bornes du filament), afin de repousser les électrons issus du filament vers le centre de la pièce et de régler l’intensité du faisceau; c'est le Wehnelt . La haute tension appliquée entre l’anode et la cathode accélère fortement les électrons vers l’anode ( ou anti-cathode ) ; ceux-ci viennent donc la heurter. L’émission des rayons X est la conséquence des interactions entre les électrons projectiles et les atomes de la cible (l’anode) On observe deux types d’interactions celle des e- projectiles avec les e- des atomes cibles : spectre de raies celle des e- projectiles avec noyaux des atomes cibles : spectre continu Finalement seulement 1% environ de l’énergie cinétique totale des électrons est convertie en RX : la quasi-totalité de l’énergie cinétique est convertie en chaleur dans la cible qui doit être refroidie (refroidissement par circulation d’huile et par rotation de l’anode). En agissant sur le rhéostat (résistance réglable) on fait varier l’intensité du courant de chauffage de la cathode donc le débit d’électrons émis par la cathode c’est-à-dire l’intensité I du courant traversant le tube entre anode et cathode. En agissant sur la haute tension UAC on fait varier la vitesse des électrons projectiles. Pour obtenir des RX de haute énergie ( plusieurs MeV ) utilisés en radiothérapie, l’accélération du faisceau d’électrons par une haute tension n’est pas suffisante et il faut recourir à des accélérateurs de particules chargées ( voir cours de 2éme année ) Cours MAHEU 2007-08 : IMRT1 – Production de rayons X PAGE 4 sur 9 3. Spectre d’émission d’un tube à RX 3.1. Allure du spectre Cas d’une cible de cuivre 1 3 2 1 3 2 Au spectre continu (courbe continue) se superpose un spectre de raies (pics étroits) caractéristiques de la cible (anode) et indépendant de la tension d’accélération. On peut noter plusieurs longueurs d’ondes remarquables : Une longueur d’onde minimale ( correspondant à une énergie maximale des photons X ) Une longueur d’onde m pour laquelle le débit de photons N est maximal ; elle est donnée par la relation m 1,5.o Des longueurs d’onde bien précises correspondant à un spectre de raies. 3.2. Interprétation du spectre continu 3.2.a. Rayonnement de freinage L’électron ( charge négative ) est dévié et freiné quand il passe à proximité d’un noyau de la cible ( charge positive ). Il perd alors de l’énergie cinétique qui est convertie en énergie électromagnétique par émission d’un photon X. + On a par conséquent : Ec (eavant freinage ) Ec (e après freinage) E( photonX émis) . Ce rayonnement de freinage est appelé en allemand « Brehmstrahlung » Cours MAHEU 2007-08 : IMRT1 – Production de rayons X PAGE 5 sur 9 3.2.b. Longueur d’onde minimale du spectre continu le photon de freinage émis a une énergie maximale h donc une longueur d’onde minimale : ceci correspond au cas où l’électron projectile perd la totalité de son énergie cinétique EC, convertie en rayonnement, en interagissant avec un noyau cible : h = EC Quelle énergie cinétique a un électron projectile quand il atteint l’anode ? Si on fait le bilan des AM s’exerçant sur un électron lors de son accélération, il est soumis à deux AM à distance : Son poids P m.g L’attraction électrique F e.E de l’anode, due au champ électrique E existant entre la cathode et l’anode. Ce champ a pour expression E U AC , d étant la distance d entre anode et cathode ( ainsi, on peut augmenter ce champ électrique en augmentant la tension U AC entre anode et cathode, ou en diminuant la distance d entre celles-ci ). On peut tout d’abord montrer que le poids est négligeable devant la force électrique. En effet P 9,11.1031.9,81 8,9.1030 N 1029 N et , pour un tube par exemple de tension U AC = 10 kV et de distance entre électrodes d = 20 cm = 0,20 m, E 10.103 50.103V / m 0, 20 et F 1,6.1019.50.103 8,0.1015 N 1014 N . Cette force est 1015 fois plus élevée que le poids !!!! On va donc considérer que le poids est totalement négligeable devant la force électrique. Appliquons donc le théorème de l’énergie cinétique pour le trajet d’un électron entre anode et cathode ( la force électrique est alors constamment parallèle au déplacement et constante ). EC A ECC e.E.d .cos(0) e.E.d e. U AC .d eU . AC d L’électron projectile de charge - e, émis avec une vitesse nulle de la cathode C ( donc ECC 0 ) et soumis à la tension accélératrice UAC, atteint l’anode A avec l’énergie cinétique : EC = e.UAC . Si toute cette énergie cinétique est convertie en rayonnement C C h o h. eU . AC soit : o h. (relation de DUANE et HUNT) eU . AC o Ce cas est un cas limite ( toute l’énergie cinétique de l’électron transformée en énergie d’émission du photon X ), mais ce n’est pas le cas de tous les photons émis : on a donc h émis h o soit émis o et donc émis o Tous les photons de longueurs d’onde supérieures à sont représentés dans le rayonnement émis qui a donc un spectre continu. Comment peut-on modifier le spectre continu ? Par variation de la tension accélératrice des électrons UAC : par exemple, les courbes sont obtenues en diminuant la tension accélératrice UAC (d’après la relation de DUANE et HUNT, la longueur d’onde limite augmente et hdiminue, ) Cours MAHEU 2007-08 : IMRT1 – Production de rayons X PAGE 6 sur 9 Par modification de la température de la cathode : par exemple, les courbes sont obtenues en augmentant la température de la cathode ( l’intensité du courant de chauffage augmente , le nombre d’électrons émis également et celui de photons du fait du bombardement plus intense de l’anode ) Exercice 2-1 3.3. Interprétation du spectre de raies Les électrons liés d’un atome sont répartis sur des couches ou niveaux. Pour arracher un électron d’une couche donnée c’est-à-dire ioniser l’atome, il faut fournir l’énergie d’ionisation qui est d’autant plus grande que l’électron est lié et donc plus proche du noyau (électron interne). D’autre part plus un électron est lié et plus son énergie est négative : L’énergie E d’un électron sur une couche est d’autant plus négative que son énergie de liaison W = -E est grande. Niveau0 : ionisation Couche M L Couche L K K Couche K 1ère couche (la plus proche du noyau) W1d’accélération est suffisante, les électrons projectiles peuvent ioniser certains Si la tension atomes cibles : sous l’effet du choc d’un électron projectile avec un atome cible, un électron lié de l’atome cible est arraché, libérant une case quantique. Un électron lié d’une couche supérieure vient alors combler la place laissée vacante par l’électron arraché. Cet électron lié se retrouve sur une couche plus basse, perd de l’énergie qui est libérée sous forme d’un photon X d’émission. Le réarrangement électronique de l’atome cible peut faire intervenir plusieurs électrons liés en cascade et produire plusieurs photons (par exemple : ionisation électron K, suivi de électron L K , suivi de électron M L…etc) La différence des énergies de liaisons d’un électron lié qui vient occuper une couche plus basse correspond à une énergie bine précise E d’un photon X émis, donc à une raie du spectre d’émission de la cathode , qui ne dépend que de la nature des atomes constituant la cathode. Sur le spectre fourni Si un électron de la couche K est arraché ( ionisation de la couche K ), on détectera les raies suivantes : h. (raie K ) WK WL ; h. ( raie K ) WK WM ; h. ( raie L ) WL WM etc… Si un électron de la couche L est arraché ( ionisation de la couche L ), on détectera les raies suivantes : h. (raie L ) WL WM ; h. (raie M ) WM WN etc… Comment peut-on modifier le spectre de raies ? Cours MAHEU 2007-08 : IMRT1 – Production de rayons X PAGE 7 sur 9 La seule possibilité est de changer le métal de l’anode, car ce spectre est caractéristique des niveaux d’énergie de ses atomes. Par exemple : les raies K et K n'apparaissent pas sur le spectre 3 obtenu avec une tension UAC trop faible pour ioniser la couche K. Exercice 2-2 (IMRT 2001 Seinographie ou mammographie ) Bilan énergétique d’un tube à RX 4. 4.1. Rendement énergétique A. Rendement : Puissance électrique consommée : PE = UAC.I ( en négligeant la puissance absorbée pour le chauffage de la cathode ) Puissance rayonnée : PR = K.Z.I.UAC2 (formule applicable dans un intervalle de tension donné) K = constante caractéristique de la cible Z = numéro atomique des atomes cible I = intensité du courant entre anode et cathode UAC = tension entre anode et cathode Puissance perdue en chaleur dans la cible par effet joule : PJ = PE - PR P K.Z.I.U AC 2 Rendement énergétique : = R = = K.Z.UAC U AC .I PE QCM Q1 questions 3,4,5,6 et 8 session 2005 B. Choix et constitution de la cible : On peut augmenter le rendement en choisissant une cible à numéro atomique Z élevé. Comme la majeure partie de l’énergie électrique consommée est convertie en chaleur, la cible doit également avoir une température de fusion élevée pour éviter de fondre. Le métal tungstène (W) est le plus souvent utilisé (Z = 74 ; Tfusion = 3700K ) La cible de tungstène est entourée de cuivre, bon conducteur thermique pour évacuer la chaleur produite 4.2. Augmentation de température de la cible Relation de la calorimétrie : Un corps de masse m dont la température varie de 1 à 2 échange avec l’extérieur la quantité de chaleur Q donnée par la relation: Q = m.c.(2 - 1) = m.c. Unités : Q en Joules ( J ) ; m en kg ; .(2 - 1) en °C ou en Kelvins c = capacité thermique massique du corps en J.kg-1.K-1 Le corps s’échauffe (2 > 1 ou >0) donc absorbe de l’énergie (Q>0) Le corps se refroidit (2 < 1 ou <0) donc cède de l’énergie (Q <0) Remarque : La température se repère en degrés Celsius, et se mesure en Kelvin (unité S.I.) T(K) ≈ (°C) + 273,15 donc T(K) = °C) Applications (voir exercices) Cours MAHEU 2007-08 : IMRT1 – Production de rayons X PAGE 8 sur 9 Q(cible) m.c Si la cible est seule: Q(cible) = PJ = PE – PR alors excessive (destruction de la cible) Avec du cuivre autour de la cible : Q(cible) + Q(cuivre) = PJ = PE – PR donc Q(cible) = PJ – Q(cuivre) alors Q(cible) << PJetmodérée Problèmes de synthèse : Exercice 2-3 ( Pb 2 : IMRT 2001 ) Exercice 2-4 Exercice 2-5 Cours MAHEU 2007-08 : IMRT1 – Production de rayons X PAGE 9 sur 9