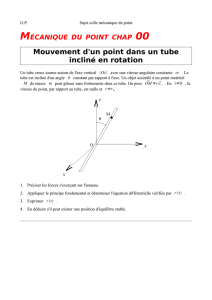
Exercices ( 25 points )

IMRT1 Evaluation n°2 22 janvier 2010 Page 1 sur 3
Données numériques : charge élémentaire :
19
1,6.10 C
célérité de la lumière
81
3,0.10 .ms
constante de Planck :
34
6,62.10 .h J s
Tungstène : symbole : W ; numéro atomique Z = 74 ; masse volumique
43
2,0.10 .
Wkg m
;
capacité thermique massique:
11
130 . .
W
C J kg K
; température de fusion : 3410°C
Cuivre : symbole : Cu ; numéro atomique Z = 29 ; masse volumique
43
8,9.10 .
Cu kg m
;
capacité thermique massique :
11
385 . .
Cu
C J kg K
; température de fusion : 1083 °C
Molybdène : symbole : Mo ; numéro atomique Z = 42 ; ; masse volumique
33
10,2.10 .
Mo kg m
;
capacité thermique massique :
11
250 . .
Mo
C J kg K
; température de fusion : 2610 °C
Cours ( 15 points )
A- Questions et applications de cours ( 9 pts )
1) Le moteur d’une perceuse sans fil est alimenté par une batterie d’accumulateurs sous une tension
constante égale à 14,4 V.
a- La puissance maximale du transfert d’énergie des accumulateurs au moteur est égale à
16W. La puissance utilisable par le moteur pour les actions mécaniques est alors de 7,0W.
Calculer dans ces conditions le rendement du moteur et l’intensité du courant qui le
traverse.
b- On se sert de cette perceuse en visseuse pour insérer une vis dans une cheville. Il faut
3,0 secondes pour la visser totalement et l’intensité du courant qui traverse le générateur
vaut alors en moyenne 820 mA.
Calculer l’énergie cédée par le générateur au moteur.
c- On s’en sert maintenant pour visser une vis de dimensions bien plus importantes. Le
moteur est bloqué et on perçoit un dégagement de chaleur relativement important. Donner
une explication.
2) Un rayonnement polyénergétique est constitué de deux raies X de longueurs d’onde
10,16 nm
et
20,45nm
, de flux de photons respectifs N1 et N2 . Sa puissance de rayonnement est P = 5,4 W .
Le flux N2 est le triple du flux N1 .
a- Calculer les énergies E1 et E2 associées à
1
et
2
.
b- Calculer alors N1, N2 et le flux total de photons X émis par ce rayonnement.
3) Une source ponctuelle de puissance Ps = 1,5 W émet un rayonnement monochromatique de longueur
d’onde  = 5,7 nm. Calculer l’intensité énergétique I et la puissance Pc reçue par une cible de surface
utile s = 20 cm2 située à 3,20 m de la source.
B- QCM ( 6 points )
Chaque question possède au moins une proposition vraie. Choisir la ( ou les ) proposition(s) vraie(s)
en recopiant, pour chaque proposition, la lettre a,b,c,d,…qui lui correspond.
Justifier chaque application numérique en indiquant l’expression littérale utilisée .
1) Un tube de Coolidge :
a- Produit un faisceau X formé essentiellement de photons de freinage
b- Produit un faisceau X émis uniquement dans la direction perpendiculaire à la cible
c- Produit un faisceau X formé essentiellement d’électrons de freinage
d- Produit un spectre de raies X caractéristiques de l’élément cible.
IMRT1 - 2009-2010 Evaluation n°2 22/01/2010

IMRT1 Evaluation n°2 22 janvier 2010 Page 2 sur 3
2) Dans un tube de Coolidge, la puissance totale rayonnée:
a- Dépend moins de l’intensité du courant d’alimentation du tube que de la tension
accélératrice
b- Est indépendante de la nature de l’anticathode
c- Dépend de la forme de l’anticathode
d- Dépend du nombre d’électrons arrivant par seconde sur l’anode
`
3) Des photons d’ énergie 100 keV sont émis avec une puissance égale à 3 mW.
a- Le nombre de photons émis est égal à
12
1,87.10
par seconde
b- Le nombre de photons émis pendant 20 secondes est égal à
12
3,75.10
c- L’énergie émise par le tube pendant 20 secondes est égale à 600 mJ
d- L’énergie émise par le tube pendant 20 secondes est égale à 0,060 J
e – les photons sont des photons X
Réponse(s) à justifier
Exercices ( 25 points )
Exercice 1 : Electricité et chauffage ( 8 pts )
Par temps de pluie, un campeur frigorifié souhaite faire chauffer au plus vite sa soupe . Pour cela, il
dispose de deux petites résistances chauffantes. Elles sont prévues pour être alimentées par une batterie
d’accumulateurs d'automobile ( de tension constante U = 12 V ).
On donne les valeurs des résistances : R1 = 13,4  et R2 = 10,9 .
Le campeur décide d’utiliser les deux résistance en même temps. N’ayant pas eu la chance de suivre votre
somptueux enseignement d’électricité, il hésite entre deux branchements :
→ Branchement 1 : Les deux résistances branchées en série sont alimentées par la batterie
→ Branchement 2: Les deux résistances branchées en dérivation sont alimentées par la
batterie
1) Représentez les circuits correspondant à ces deux branchements.
2) Pour chaque branchement, déterminez ( dans l’ordre de votre choix ) : la tension aux bornes de
chaque résistance chauffante, l’intensité du courant qui les parcourt ( fléchez et nommez les grandeurs
électriques étudiées et citez les lois de l’électricité utilisées pour votre raisonnement )
3) En déduire la puissance de chauffe totale des deux résistances ; concluez sur le meilleur branchement
à adopter .
Exercice 2 Emission de rayons X ( 7 pts )
On donne en annexe le spectre d’un tube à rayons X avec anode en cuivre.
1) Expliquez de quelle façon apparaît le spectre continu et pourquoi ce spectre est continu
2) Expliquez de quelle façon apparaissent les raies du spectre .
3) Déterminez la longueur d’onde minimale et la longueur d’onde la plus probable du spectre (Justifier ).
4) Sans modifier la tension entre anode et cathode, on augmente If le courant d’alimentation du filament.
Expliquez ce que cela modifie et tracez sommairement le nouveau spectre sur le graphe de l’annexe
( justifier )
Exercice 3 Radiodiagnostic classique ( d’après DTS IMRT session 2001 ) ( 10 pts )
Dans un tube utilisé pour ce genre de diagnostic, le tube à rayons X est alimenté par une tension variant
entre 60 et 120 kV.
1) Pour un examen, on utilise une tension U = 80 kV. Un courant de 40 mA traverse alors le tube.
a- Calculer le nombre d’électrons arrivant sur l’anode en 0,5 s, durée d’une radiographie.
b- Quelle est l’énergie cédée par l’ensemble de ces électrons lorsqu’ils sont arrêtés par
l’anode ? ( donner le résultat dans le SI d’unités )

IMRT1 Evaluation n°2 22 janvier 2010 Page 3 sur 3
2) Pour une tension de 80 kV, le rendement du tube est = 0,8%. Quelle est la puissance d’émission du
faisceau de rayons X ? Quelle énergie fournit-il pour une radiographie qui dure 0,5 s ?
3) Une grande partie de l’énergie consommée par le tube n’est pas restituée sous forme de rayons X :
a- Sous quelle forme cette énergie apparaît-elle ?
b- Quelle énergie est ainsi dissipée pour une radiographie qui dure 0,5 s ?
c- Quelle élévation de température subit alors l’anode ( considérée comme un bloc de
tungstène de section S = 6,0 cm2 et d’épaisseur e = 1,5 mm ) ? Cette valeur vous paraît-elle
supportable pour le matériau utilisé ?
d- Partant de 20°C, on souhaite que la température de l’anode ne dépasse pas 100 °C. On
utilise donc un dispositif de refroidissement ; déterminer la chaleur que doit prélever ce
système durant la radiographie.
e- Le système de refroidissement étant un bloc de cuivre entourant l’anode, quelle doit être
sa masse ?
4) Déterminer le rendement et la puissance d’émission qu’aurait ce tube pour une tension d’alimentation
de 120 kV et avec une anode en molybdène ( le courant dans le tube étant inchangé ).
NOM : Prénom :
IMRT1 - 2009-2010 Evaluation n°2 22/01/2010
ANNEXE à l’exercice 2 – A rendre avec votre copie
E0 = 20 keV