1.8 Mo - La Cosmologie précise, par Philippe Magne

1
ÉPISTÉMOLOGIE
Modèle actuel d’univers basé sur la « Concordance »
Philippe Magne
2007

2
Avant propos
Peut-on vraiment définir l’objectif d’une investigation de l’Univers ?
Le mot Univers désigne un tout, un tout entier.
De prime abord on peut se demander si cette ambition n’est pas démesurée ?
Il faut cependant constater que l’enthousiasme des chercheurs concernant l’Univers
n’a jamais faibli pendant des siècles, rien n’a pu l’arrêter !
La rigueur oblige cependant, dans un premier temps, à se limiter au volume que l’on
peut observer ( je crois ce que je vois ! ), mais l’évolution des idées permettra peut
être de déduire quelque chose de plus vaste.
Le risque est une dérive métaphysique préjudiciable au dialogue entre théoriciens,
observateurs, et expérimentateurs.
Ce dialogue, pour être fructueux, nécessite que les échanges se fassent de façon
numérique, traitables par l’informatique.
De cette façon, on peut espérer une cosmologie précise.
Que veut dire précise ?...que les paramètres du modèle contiennent une partie
décimale copieuse, l’incertitude et le taux de confiance étant, par ailleurs, définis.
Méthode
Avant d’entrer dans le vif du sujet, il est bon de rappeler comment un domaine de la
connaissance progresse par la conjonction de théories, d’observations et
d’expériences.
C’est en discernant des liens, en construisant un modèle, sorte de schéma voulu
aussi simple que possible.
Avec un peu de chance on aboutit à quelque chose de nouveau en constatant les
concordances des résultats de mesures.
Abécédaire
La Cosmologie est la science des lois générales qui gouvernent l’Univers.
La Cosmogonie concerne la formation des objets célestes.
Ces deux domaines de recherches sont souvent menés de concert dans un cadre
relativiste et quantique.
Il arrive que ce cadre, lui aussi, bénéficie de contradictions qui peuvent surgir du fait
de la mise en modèle, bien que le but soit de mettre en évidence des concordances.

3
Modèle actuel de l’Univers
Ce qui prime, c’est l’indissociabilité de la matière / énergie et de l’espace-temps en
interaction permanente.
« La matière dicte à l’espace-temps sa courbure et l’espace-temps dicte son
mouvement à la matière, selon Archibald Wheeler, un physicien relativiste de
grand renom »
Quand on évoque l’expansion de l’Univers, c’est en fait la dilatation de l’espace lui
même dont il s’agit.
La tactique est de faire usage de ce que l’on appelle « le référentiel comobile » qui
permet d’inclure l’immobilité dans un espace qui lui, est mobile.
Plus clairement, les coordonnées des concentrations de matière sont constantes
dans ce référentiel, bien que la distance métrique entre points ne cesse de croître.
C’est aussi une façon d’exprimer que la répartition des constellations reste
homothétique.
Egalement, le centre de l’Univers est partout et nulle part à la fois, chaque
observateur à la sensation d’être au centre de l’Univers (voir Figure 1).
Evoquons maintenant les principaux aspects du modèle conventionnel actuel.
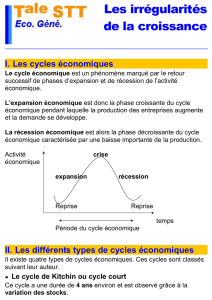
 L’Univers est isotrope et homogène
 L’espace-temps est quadridimensionnel et en expansion accélérée
Pour n’importe quel observateur situé à l’origine d’un référentiel comobile les
agrégats de matière ont une vitesse de récession proportionnelle à la
distance, cette vitesse peut dépasser largement la vitesse de la lumière.
En ce qui concerne la matière et l’énergie, le modèle prend en compte la
matière qui émet de la lumière et aussi celle qui n’en émet pas, dite noire.
De même pour l’énergie répulsive, cause de l’accélération de l’expansion et
qui n’émet pas de lumière, elle est dite noire, on n’en connaît pas la nature ,
certains lui donne le nom de quintessence ( cinquième élément des Grecs
dans l’histoire ancienne )
 La vitesse de la lumière, invariant, et qui est indépassable, prônée par la
Relativité Restreinte, est une propriété locale conservée dans le modèle, mais
ne s’applique pas à la gravitation. La Relativité Générale résout le problème
en assimilant la gravitation à une courbure de l’espace-temps (la grande idée
d’Einstein déduite de son principe d’équivalence )
 Du fait de l’expansion, la lumière émise par un corps céleste puis reçu par un
observateur implique :
une distance d’émission par rapport à l’observateur, celle à laquelle se
trouvait ce corps céleste au début de l’ émission, plus petite que la distance
de réception, celle à laquelle se trouve ce corps céleste au moment de la
réception ( aujourd’hui )
« La lumière ressemble à un coureur sur une piste qui s’étirerait et dont
le poteau d’arrivée reculerait plus vite qu’il ne peut courir selon Arthur
Edddington »

4
 L’expansion étire les longueurs d’onde comme elle le fait pour l’espace, on
l’exprime par le red-shift (décalage vers le rouge) noté z.
 Le géniteur de la matière est assimilable à un corps noir de Planck à très
haute température et densité considérées comme infinies, c’est une
singularité de l’espace-temps que l’on prend arbitrairement comme origine de
la coordonnée temps cosmique.
La physique ne peut rien dire au delà de 1032 K.
Le Big Bang émerge de cette singularité après une période d’inflation
exponentielle de l’espace qui dure 10-32 seconde.
On peut imaginer qu’au sortir de la singularité existe un nuage de photons qui
s’entrechoquent comme le font les particules de nos accélérateurs.
Ce milieu est opaque à la lumière du fait de son extrême densité, il dégénère
en plasma après la nucléosynthèse. Les oscillations de ce plasma engendrent
des zones à plus haute pression et à plus basse pression, l’instabilité
gravitationnelle forme des grumeaux qui s’assembleront plus tard pour former
les grandes structures constituées de galaxies.
Aujourd’hui ces grandes structures ont un diamètre d’environ100 millions d’AL
les galaxies, plus petites, qui les composent, en général en rotation, auront
acquis ce mouvement par suite d’effets de viscosité.
Toute la matière cosmique baigne dans un reliquat du corps noir déjà cité qui
a considérablement refroidit, sa température actuelle est de 2.725 K, il se
manifeste comme un bruit de fond « cosmique » que l’on capte en ondes
millimétriques ( encore appelé « fond diffus cosmologique » )
 Revenons à l’évolution de l’Univers, elle s’est faite de la façon suivante.
Tandis que l’espace se dilatait, la température baissait, et lorsqu’elle atteignit
3000 K les protons purent capturer les électrons, c’est ainsi que se forma
l’hydrogène primordial.
C’est aussi ainsi que l’Univers devint transparent, lorsque la durée de libre
parcours des photons devint supérieur à l’âge de l’Univers à cette époque,
environ 370000 ans après le Big Bang mot « canular » inventé jadis par les
détracteurs du modèle en expansion, spécialistes et public l’ont adopté par la
suite (Figure 2)
 Quelles sont les contraintes pour le modèle actuel de l’Univers ?
Il faut que le calcul de son âge soit supérieur à l’âge des plus vieilles étoiles
que les astrophysiciens savent calculer à partir de la mécanique quantique.
Une autre contrainte est l’abondance relative des éléments légers qui se sont
formés, après la nucléosynthèse primordiale, tels que l’hydrogène, le
deutérium, l’hélium …etc …

5
Paramètres du modèle
Deux constantes sont essentielles et ont une origine observationnelle.
La constante Universelle de la Gravitation de Newton (CUG) :
G = 6.6729 x 10-11 m3 / kg x s2
La constante de proportionnalité vitesse de récession / distance, constante dans tout
l’espace mais pas dans le temps, c’est la constante de Hubble, au temps présent elle
vaut : H0 = 71 km / s x Mpc
Mpc veut dire Mégaparsec soit 106 parsecs soit 3.084 x 1022 m soit 3.26 x 106 AL
0
1
H
est homogène à un temps et vaut 13.77 x 109 Années
Historiquement (voir l’Annexe 2) il fut mis en évidence une densité particulière qui
rendait la géométrie de l’espace cosmique euclidienne, elle fut appelée densité
critique
c
, au temps présent, indicée 0, elle vaut :
226 3
0
c0 3H 0.947 10 kg/m
8G 
Comme il y a 3 sortes de composantes fluidiques qui participent au champ de
gravitation, on prend comme unité de densité
c0
et on exprime alors leur densité par
la lettre indicée de la façon suivante :
Le rayonnement électromagnétique
r
rc0
La matière en général
m
mc0
L’énergie répulsive qui accélère l’expansion
c0
En gros il s’avère que la somme des trois oméga est voisine de 1
rm 1
Comme il y a une petite incertitude sur cette somme comprise ente 1 et 1.04
on a introduit un quatrième oméga :
k r m
1 ( )
qui intervient pour
évaluer une courbure (
k
est plus grand que 0 et plus petit que + 0.04)