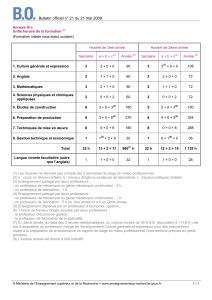
Le Directeur - Université d`Orléans

Ecole Doctorale Sciences et Technologies (E.D.S.T.) Bât. Physique-Chimie Rue de Chartres B.P. 6759 45067
ORLÉANS CEDEX 2
Filière « Mathématiques – Informatique »
Titre de la thèse : Etude des processus de transport intermittents sur des surfaces fractales
Directeurs de thèse : Athanasios BATAKIS (MdC) et Michel ZINSMEISTER (PR)
Equipe d'accueil : Laboratoire MAPMO (Mathématiques et Applications, Physique Mathématique d’Orléans)
UMR 6628, Université d’Orléans
Libellé de la Direction Scientifique Principale du thème : DSPT 1 (Mathématiques et leurs interactions)
Libellé de la Direction Scientifique Secondaire du thème :
Libellé de la Discipline par rapport à la Direction Scientifique Principale : 101 (Mathématiques et leurs
interactions)
Type d’allocations : EDST
Exposé du sujet : Les processus de transport intermittent ont été proposés par des physiciens (Levitz,
Benichou) et des biologistes (Fourcassier) afin de modéliser des procédés aussi variés que la recherche de
nourriture par les animaux ou la quête d’un site cible par les protéines de l’ADN.
Ces processus consistent de deux phases : Une phase, généralement appelée « lente », correspondant à la
période durant laquelle le chercheur se trouve en contact étroit avec l’interface hébergeant la cible et est
susceptible de la trouver et une phase, dite « rapide », durant laquelle le chercheur se déplace pour se
repositionner à un autre endroit de l’interface et recommencer sa recherche.
Les deux phases sont décrites par des processus aléatoires : la deuxième par le mouvement Brownien dans
l’espace environnant et la première par un processus de diffusion sur l’interface. Nous sommes intéressés par
les statistiques de ces déplacements, i.e. les distances parcourues sur l’interface et en dehors et le temps
nécessaire pour les parcourir. Des résultats concernant la phase de déplacement « rapide » sont d’ores et déjà
rigoureusement établis dans un article de nous-mêmes avec P. Levitz.
L’objectif de cette thèse est l’étude du couple [déplacement « rapide »-déplacement « lent »] dans le cas ou
l’interface est fractale (par exemple un tapis de Sierpinski) quand la durée de la première phase est décrite par
une loi de type Poisson. Il faudra commencer par faire le lien avec les processus de diffusion sur les fractals
introduits par Kigami et Lapidus afin d’étudier les statistiques du couple : durée de chaque phase et longueurs
des déplacements, étendue de la zone visitée.
Le sujet est à l’intersection de la théorie du potentiel (probabiliste) et des systèmes dynamiques ; l’étude
théorique devra être accompagnée par une simulation numérique des objets. Par ailleurs, l’avancement de la
thèse sera solidement épaulé par des résultats expérimentaux fournis par les équipes de physiciens et de
biologistes avec lesquelles nous sommes en contact.
Emails des directeurs de thèse : at[email protected],
Lien éventuel avec un pole de compétitivité, avec le projet Soleil, le cancéropole grand Ouest ou le pôle
d'efficacité énergétique:

2
Répartition des disciplines et GER par Direction Scientifique Pédagogique et Technologique Annexe 1
Nouveau
DSPT
Libellé
DSPT
CODE
RSD
LIBELLE RSD Regroupement de Secteurs Disciplinaires
ou GER Groupes d'Experts Recherche
CODE
DISCIPLINE
LIBELLE DISCIPLINE
DSPT 1
mathématiques et leurs interactions
10
Mathématiques et leurs applications
101
Mathématiques et leurs interactions
DSPT2
Physique
20
Physique et science des matériaux (provisoire)
211
Milieux denses, matériaux et composants
21
Milieux denses, matériaux et composants
221
Constituants élémentaires et physique théorique
22
Constituants élémentaires, physique théorique, plasmas chauds
222
Plasmas chauds
23
Milieux dilués et optique fondamentale
231
Milieux dilués et optique fondamentale
DSPT 3
Sciences de la Terre et de l'Univers,
Espace
30
Sciences de la Terre et de l'Univers ; Espace, Sciences de l'environnement
301
Astronomie, astrophysique
302
Terres solides et couches profondes
303
Terres solides et enveloppe superficielle
304
Terres, enveloppe fluide
DSPT 4
Chimie
40
Chimie et science des matériaux
401
Chimie théorique, physique, analytique
402
Chimie organique, minérale, industrielle
403
Chimie des matériaux
404
Génie des matériaux
DSPT 5
Biologie Médecine, Santé
51
Aspects moléculaires et cellulaires de la biologie
510
Aspects moléculaires et cellulaires de la biologie
52
Physiologie et biologie des organismes
520
Physiologie, Biologie des organismes, populations, intéractions
53
Biomolécules, Pharmacologie, Thérapeutique
530
Biomolécules, pharmacologie,thérapeutique
DSPT8
Sciences pour l'Ingénieur ( Sciences
de la mécanique et de l'énergie,
Génie des procédés et de la
Production, Génie électrique,
Transports - Génie civil)
81
Mécanique des solides, des matériaux et des surfaces
811
Mécanique des solides, des matériaux, des structures et des surfaces
812
Génie civil
813
Génie mécanique, productique, transport
82
Mécanique des fluides, énergetique, thermique, combustion, acoustique,
bio-mécanique, bio-ingénérie
821
Mécanique des milieux fluides
822
Energétique, thermique, combustion
823
Acoustique
824
bio-mécanique, bio-ingénérie
83
Génie des procédés, plasmas froid
831
Génie des procédés
832
Plasmas froids
84
Génie électrique, , électronique de puissance
841
Génie électrique (utiliser un 840 provisoirement pour ventiler l'ancien 430)
842
Electronique de puissance
DSPT9
Sciences et technologies de
l'information et de la
communication (incluse
l'informatique)
91
Informatique et applications
911
Informatique et applications
92
Automatique, traitement du signal
921
Automatique, productique
922
Traitement du signal et des images
93
Electronique, photonique
931
Electronique, microélectronique et nanoélectronique
932
Optoélectronique, micro-ondes
933
Optique appliquée et lasers
DSPT10
Agronomie, Production animales et
végétales et agro-alimentaires
100
Sciences agronomiques, Biotechnologies agro-alimentaires
1000
Sciences agronomiques; biotechnologie agro-alimentaires (à ventiler par la suite)

3
1
/
3
100%