Résumé

DE LA STABILITE DES AERONEFS AVEC AILES EN TANDEM
Une approche théorique et numérique des coefficients
de stabilité de l'équilibre en vol.
Bernard GUERRAND
----------------------------
Résumé
Parmi les aéronefs à deux plans les plus répandus sont les appareils à ailes en tandem : les avions dits traditionnels
des aéroclub, les canards dont l’aile la plus grande est à l’arrière et les pou-du-ciel. De manière à préciser, quantifier puis
comparer les performances de stabilité des aéronefs de chacune de ces catégories, voire d’une catégorie à l’autre, une
méthode numérique et systématique est proposée. Cette approche de la stabilité repose sur un calcul de la dérivée du
couple de tangage par rapport à l’incidence, au voisinage du point d’équilibre. Cette grandeur « dM/di » est comparée aux
coefficients habituels tels le rapport des coefficients de portance (kch) ou le rapport des « volumes de stab » (. La note
expose la méthode et les applications numériques sur tableur EXCEL et les résultats obtenus sur quelques configurations,
notamment pour 3 vitesses et des conditions de centrage extrêmes. Les résultats permettent d’évaluer la sensibilité au
centrage et au profil de ces trois coefficients. Les caractéristiques aérodynamiques des profils sont implicites dans dM/di :
ce qui explique sans doute pourquoi ce coefficient est le plus efficace pour évaluer l’influence du choix des profils, du
centrage et autres données sur la stabilité.
SOMMAIRE
1 - OBJET ................................................................................................................................................................................................ 2
2 - LIMITES DE L’ETUDE ................................................................................................................................................................... 2
3 - RELATIONS DE BASE .................................................................................................................................................................... 3
3.1- FORCES ET COUPLES AGISSANT SUR L’AERONEF ............................................................................................................................ 4
3.1.1 - Force d’inertie ..................................................................................................................................................................... 4
3.1.2 - Forces Aérodynamiques exercées sur chaque aile ............................................................................................................... 4
3.1.3 - Force motrice ....................................................................................................................................................................... 4
3.1.4 - Moment des Forces .............................................................................................................................................................. 5
3.2 - EQUILIBRE DU VOL ........................................................................................................................................................................ 5
3.3 - STABILITE DU VOL ........................................................................................................................................................................ 5
4 - EQUATIONS A RESOUDRE ET COEFFICIENTS DE STABILITE ........................................................................................ 6
4.1 - EQUATIONS A RESOUDRE POUR OBTENIR L’EQUILIBRE ................................................................................................................. 6
4.2 - GRANDEURS DE STABILITE A CALCULER ET CRITERES A EVALUER ............................................................................................... 6
4.2.1 - Grandeur de stabilité par dérivée du moment de tangage dM/d ....................................................................................... 6
4.2.2 - Grandeur de stabilité par rapport des Cz : kch .................................................................................................................... 7
4.2.3 - Grandeur de stabilité par rapport des volumes de stab : ................................................................................................. 7
5 - METHODE DE RESOLUTION ...................................................................................................................................................... 8
5.1 - METHODE ..................................................................................................................................................................................... 8
5.2 - FEUILLES DE DONNEES ENTREES SORTIES EXCEL ....................................................................................................................... 9
5.3 - FEUILLE « CALCULS » ................................................................................................................................................................. 10
5.4 - FEUILLE « AILE K » ..................................................................................................................................................................... 11
6 - RESULTATS DES CALCULS ....................................................................................................................................................... 12
6.1 - CONFIGURATION POU DU CIEL .................................................................................................................................................... 12
6.1.1 - TWIN avec deux NACA 23012 .......................................................................................................................................... 12
6.1.2 - TWIN avec deux NACA 23112 ......................................................................................................................................... 13
6.1.3 - TWIN avec deux CLARK Y ................................................................................................................................................ 14
6.2 - CONFIGURATION AVION ........................................................................................................................................................... 15
7 - SYNTHESE ..................................................................................................................................................................................... 16
7.1 - QUEL COEFFICIENT CHOISIR ?...................................................................................................................................................... 16
7.2 - COMPARER LES STABILITES D’UNE CONFIGURATION A L’AUTRE ................................................................................................. 16
8 - CONCLUSION ................................................................................................................................................................................ 17

2
1 - OBJET
Les aéronefs plus lourds que l’air volent en transmettant à l’air les forces dues principalement à la pesanteur. Cette
transmission peut se faire avec une aile tournante d’hélicoptère, une aile fixe comme celle du concorde, ou plusieurs :
ailes en tandem, biplans, multi-surfaces etc.
Le cas des ailes en tandem comprend au moins trois catégories :
 les avions de type grand monoplan à l’avant et petit stabilisateur arrière : la plus répandue
 les canards qui ont l’aile la plus grande à l’arrière,
 les pou-du-ciel.
La connaissance des propriétés de stabilité de ces aéronefs vient la plupart du temps de l’expérience associée à des
calculs de critères simplifiés. Réaliser des comparaisons de stabilité amène alors à ajouter aux incertitudes des essais, des
hypothèses incertaines sur le calcul de ces critères. De manière à réduire ces incertitudes dans l’évaluation des
performances de stabilité des appareils de chacune de ces catégories, voire d’une catégorie à l’autre, une méthode
numérique et systématique a été développée. Cette approche par le calcul traite explicitement de l’impact d’une
perturbation de l’incidence sur le couple de rappel vers l’équilibre. Cet impact est un calcul de la dérivée du couple par
rapport à l’incidence au voisinage du point d’équilibre.
L’objet de la note est de présenter :
 les définitions des grandeurs et les relations physiques qui les relient,
 les lois de l’équilibre et de la stabilité,
 l’approche numérique : algorythmes et développements des calculs
 les résultats de calculs de stabilité obtenus sur des configurations d’ailes en tandem.
 une étude comparative des résultats et des différents coefficients de stabilité habituels
2 - LIMITES DE L’ETUDE
Axe de tangage
Sur l’axe de lacet les conditions d’équilibre et de stabilité sont conditionnées par les surfaces des dérives et aussi par
celles du fuselage.
L’étude présentée ici est limitée à la stabilité en tangage c’est à dire aux conditions nécessaires au rappel en piqué si
la perturbation est à cabrer. Dans ce domaine, le fuselage joue un rôle négligeable par rapport aux surfaces horizontales
des ailes ou des stabilisateurs : c’est pourquoi le fuselage est négligé dans cette étude.
Configuration Pou du Ciel
Les calculs sont réalisés sur la configuration pou du ciel dessiné et construit avec deux de mes amis : TWIN AIR.
Les ailes sont dérivées du modèle AIRPLUME n°10 de E.CROSES, tandis que la cellule est un biplace côte à côte
entièrement originale et large de 1.15 m au maître couple. Cette géométrie est la même pour les différents cas étudié de
manière à pouvoir comparer l’influence de la nature des profils sur la stabilité toute choses égales par ailleurs, pour trois
vitesses, un centrage avant et un centrage arrière.
Configuration AVION
Les calculs sont réalisés sur la configuration d’un avion de construction amateur aussi : le MENESTREL biplace
HN700 II.
Remarque : C’est une pratique courante que de comparer ce qui n’est pas « égal par ailleurs », par exemple la
stabilité de deux voitures de marque différente alors que les capacités de chargement et les domaines d’évolution sont
différents. Le résultat de ces comparaisons est à prendre avec précautions. En aéronautique c’est encore plus vrai, du fait
du déplacement sur les trois axes, des capacités de maniabilité différentes ou encore plus simplement de la plage de
vitesse. Cependant, de manière à pouvoir comparer les valeurs des coefficients de stabilité la masse de la configuration
étudiée est la même que pour le pou du ciel et le domaine de vitesse sera voisin.

3
3 - RELATIONS DE BASE
Trièdre et Notations
Un trièdre aérodynamique (G, x, y,z) est défini à partir de G, centre de gravité de l’aéronef, pour situer dans l’espace
les objets réels et les grandeurs physiques destinées à modéliser les phénomènes :
 Axe de roulis Gx : tangent à et dans le sens de la vitesse relative de l’aéronef, Gx est tangent en G à la trajectoire
suivi par l’aéronef
 Axe de lacet Gz : ┴ à Gx et orienté vers les pieds du pilote
 Axe de tangage Gy : ┴ à Gx et orienté vers la droite du pilote
Les notations et unités des grandeurs sont indiquées dans le tableau 1.
Tableau 1 - Notation et unités des grandeurs
NOM des Grandeurs
Symbole
Unité
masse avion
m
kg
masse volumique
kg/m3
Accélération de la pesanteur
g
m/s2
Vent relatif
W
m/s
Traction motrice
Tr
N
Ordonnée centre de traction
Zr
m
profil aile k
profil k
Sans
Corde aile k
Ck
m
Surface aile k
Sk
m2
Ordonnée bord attaque aile k
zk
m
Abscisse bord attaque aile k
xk
m
Incidence Aile k
ik
°
Centre de poussée aile k
Cpk
Sans
Abscisse centre de poussée aile k
Xk
m
Ordonnée centre de poussée aile k
Zk
m
Coefficient de portance aile k
Czk
Sans
Coefficient de traînée aile k
Cxk
Sans
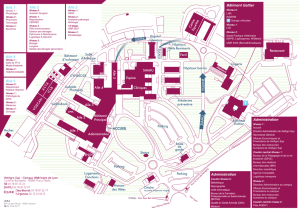
La figure 1 présente la géométrie de l’aéronef retenue ainsi que les efforts et autres couples.
Cp2
AXE DE VOL
R1
R2
i2
i1
z1
Z1
z2
Z2
G
X2
X1
x1
x2
Cp1
Fz
W
Tr
M
+
Zr
Liaisons indéformables après centrage
G
Cp1
Cp2
Cr
Cr
FIGURE 1 – Vue de profil des ailes en tandem
Cette géométrie ressemble à celle d’un pou du ciel mais est applicable à celle d’un avion.

4
La plupart des caractéristiques géométriques sont de conception. D’autres sont variables comme les incidences liées à
la vitesse, le centrage qui est la position relative de G par rapport aux ailes dans l’axe de vol.
Ce centrage est défini dans la suite par : X = x1 / CT
avec CT = x1 - x2 +C2 cos( i2 /180 )
Nota : sur les avions, on limite en général CT à la corde de l’aile avant C1.
En pratique, le constructeur calcul une incidence de vol, puis place les masses pour obtenir la bonne position de G en
supposant en première approximation i1 et i2 petits d’où CT ≡ x1 - x2 . Ce qui permet de fixer les réservoirs, le moteur et
autres masses en première approximation. Puis viennent les essais…l’étude suppose ici le même raisonnement : dans
l’ordre seront calculées les incidences i1 et i2, puis la position réelle en vol de G.
3.1- Forces et couples agissant sur l’aéronef
L’aéronef est animé d’un mouvement :
 Selon les axes du trièdre, dû à la résultante des forces supposées appliquées en son centre de gravité G
 Autour des axes du trièdre, dû au moment de ces forces par rapport à G
Etudier l’équilibre de l’aéronef revient donc à étudier ces forces et le moment de ces forces
3.1.1 - Force d’inertie
F
est fonction de la masse totale m [kg] de l’aéronef et de l’accélération de la pesanteur g .
Hypothèse H3.1.1 : Dans la suite, l’axe Gx est supposé horizontal et Gz supposé vertical.
Cette force se réduit alors à
mgFz
Fy
Fx
F0
0
(3.1.1)
3.1.2 - Forces Aérodynamiques exercées sur chaque aile
Ces forces
k
R
sont fonction de la masse volumique  [kg/m3] de l’air, de la vitesse W [m/s] , des surfaces d’ailes
(indicées k = 1 ; 2) Sk [m2] et des coefficients de traînée Cx et de portance Cz de leur profil :
kkk
k
kkk
SWCzRz
Ry
SWCxRx
R
2
2
2
1
02
1
(3.1.2)
Ces forces s’appliquent aux centres de poussée Cpk.
Remarque : par convention, si Cz est positif Rz est négatif, de même si Cx est positif Rx est négatif.
3.1.3 - Force motrice
Elle est fournie par le moteur est s’applique en Cr :
0
0
Tz
Ty
TTx
Tr
(3.1.3)

5
3.1.4 - Moment des Forces
M
est le couple des forces ci-dessus appliquées aux bras de levier correspondant par rapport à G. Sachant que les
coordonnées des centres de poussée et centre de traction sont comptées algébriquement :
rrkkkkk ZT
Mz
CzXCxZSWMy
Mx
M
0
2
1
0
2
(3.1.4)
3.2 - Equilibre du vol
La relation fondamentale de la dynamique donne :
 mTRF
 IM
où est l’accélération tangentielle, dérivée de la vitesse
l’accélération angulaire autour de Gy et I le moment d’inertie
Au point d’équilibre du vol dit « Eq » l’aéronef a une vitesse constante : les accélérations sont nulles et il suit une
trajectoire rectiligne uniforme et sachant H3.1.1 , horizontale :
0 TRF
(3.2a)
0M
(3.2b)
3.3 - Stabilité du vol
La stabilité signifie que l’aéronef s’oppose de lui-même aux perturbations.
Lorsque chaque aile voit son incidence augmenter de d, l’aéronef risque de se cabrer : pour être stable sur l’axe de
tangage, le moment des forces M doit donc augmenter d’une quantité à piquer soit dM > 0. Inversement, dM doit être <0
si d <0. L’écriture de cette stabilité se réduit alors à écrire que la dérivée du moment par rapport à l’incidence est
positive au point d’équilibre Eq.
Eq
d
dM 
0
(3.3)