Courant électrique alternatif sinusoïdal

GRISP - Académie de Créteil - 2002
TOURNEZ, TOURNEZ VECTEURS !
http://www.ac-creteil.fr/physique/DOCGRISP/Vecteurs/vecteurs-fresnel.htm
COURANT ELECTRIQUE ALTERNATIF SINUSOÏDAL
Circuit série RC ou RL
OBJECTIF :
Représentation de Fresnel pour les circuits séries résistor-capacité ou résistor-bobine
PUBLIC : Baccalauréat Professionnel ( BEP électrotechnique après simplification)
MATERIEL: PC équipé de Excel 97 (ou supérieur)
LOGICIEL: Cabri II géomètre, Excel 97 (et sup), GeoplanW
METHODE : démonstration pendant les cours et évaluation individuelle en autonomie.
AVANTAGES : modélisation plus facile pour les élèves par l'aspect dynamique des
constructions.
DIFFICULTES: bien articuler le cours entre séances de TP, démonstrations sur ordinateur,
cours, exercices, évaluations, …
AUTEUR DU DOCUMENT :
J.-P. MALEPLATE - Lycée Professionnel CHAMPLAIN - Chennevières s/ane.

GRISP - Académie de Créteil - 2002
I- INTRODUCTION DES VECTEURS DE FRESNEL EN
BACCALAUREAT PROFESSIONNEL
1) " Construire, c'est changer !" et "changer, c'est
vivre des ruptures " : l'expérience incontournable,
On peut justifier l'utilisation de la représentation de Fresnel en réalisant une expérience
simple : un circuit RC alimenté par un GBF sur lequel on mesure la tension aux bornes du
résistor, la tension aux bornes de la capacité et la tension totale (appelée "méthode des
trois voltmètres").
Les élèves se heurtent à un obstacle : la somme arithmétique des tensions n'est pas égale
à la tension totale ! Seule la somme vectorielle permet d'expliquer le phénomène. La
construction géométrique utilisant les valeurs des tensions efficaces (cf ci-dessous)
permet alors de démontrer aux élèves l'égalité vectorielle.
La méthode des trois voltmètres
Elle permet de démontrer aux élèves
les limites du champ de validité de la
loi d'additivité des tensions continues.
La relation U1 + U2 = U3 (tensions
efficaces lues sur les voltmètres) n'est
plus valable en courant alternatif.
Remarque :
Elle reste utilisable si les dipôles passifs utilisés
sont des résistors.
Figure 1
U1 + U2 = U3
Error!
+
Error!
=
Error!
En courant continu
En courant alternatif
Principe de construction
On peut construire les trois vecteurs
associés aux tensions efficaces relevées
sur les voltmètres.
Exemple :
Tension U1 U1 = 3,5 V
Tension U2 U2 = 2,8 V
Tension totale U3 U3 = 4,71 V
3,5
Error!
Error!
Error!
4,71
2,8
.
.
.
Comme nous l'explique G. de Vecchi et N. Carmona-Magnaldi dans
leur ouvrage "Faire construire des savoirs" aux édition Hachette
éducation, "Construire, c'est changer !" et "changer, c'est vivre des
ruptures".
Figure 2

GRISP - Académie de Créteil - 2002
Trois remarques importantes :
Conseil pratique pour réaliser le TP du circuit série RC :
Il faut savoir que les capacités se comportent comme un fil pour les hautes fréquences ( impédance Z =
Error!
oblige ! ). Il sera donc judicieux de choisir des fréquences suffisamment basses pour que la
tension aux bornes du condensateur soit de l'ordre de la tension aux bornes du résistor.
Selon le matériel que l'on utilise dans les différents laboratoires, ces valeurs peuvent changer. Seul la
méthode empirique permet d'ajuster la fréquence pour être dans de bonnes conditions.
A quoi ça sert ?
Les vecteurs de Fresnel sont utilisés pour modéliser le comportement des circuits RL (résistor-bobine)
équivalent aux moteurs fonctionnant en courant alternatif. Le cos  des moteurs peut être déterminé à
l'aide de la représentation de Fresnel avec une bonne précision.
On introduit également l'étude des circuits RC (résistor-capacité) pour modéliser le comportement des
capacités ( non polarisées ). Cette dernière étude pourra nous servir à expliquer l'emploi de condensateur
de démarrage sur certain moteur.
Comment relier un vecteur et une tension alternative sinusoïdale ?
C'est à ce niveau que l'on va commencer à utiliser l'ordinateur pour aider l'élève à comprendre ce modèle
des vecteurs de Fresnel.
2) Objectifs "triangulaires" à atteindre avec
l'utilisation de l'ordinateur
Les élèves doivent être
capables de relier la
représentation graphique,
l'expression algébrique et le
vecteur de Fresnel.
Ils doivent pouvoir passer
facilement de l'un à l'autre
afin de choisir celui qui
répondra le mieux au
problème posé.
Les élèves vont atteindre
des objectifs intermédiaires
et des sous-objectifs pour
pouvoir construire ces liens
entre le vecteur de Fresnel,
la représentation graphique
et l'expression algébrique.
Le tableau ci-après
récapitule ces objectifs
intermédiaires à atteindre.
Vecteur
de Fresnel
Représentation
graphique
Expression
algébrique
u(t) = U; .sin( t +  )
Figure 3 - Objectifs "triangulaires" pour la modélisation
des vecteurs de Fresnel

GRISP - Académie de Créteil - 2002
Objectifs intermédiaires
1er objectif :
admettre le modèle vectoriel pour représenter une tension alternative
sinusoïdale (longueur, vitesse de rotation, déphasage…)
2ème objectif :
évaluer la valeur du déphasage  entre deux vecteurs à partir des
tensions instantanées sur un écran d'oscilloscope.
3ème objectif :
tracer les représentations graphiques des tensions instantanées liées à
des vecteurs par simple construction géométrique.
4ème objectif :
déterminer l'expression algébrique des tensions instantanées à partir:
- des caractéristiques des différents vecteurs.
- des courbes représentatives des tensions électriques instantanées.
En déduire l'expression de l'intensité instantanée i (t) et le cos .
II - CONSTRUCTION DU MODELE DES VECTEURS
DE FRESNEL
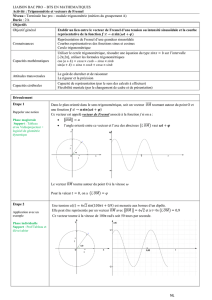
1) Représenter une tension alternative sinusoïdale
par un vecteur.
Utilisation de Cabri géomètre II pour relier tension électrique sinusoïdale et vecteur
tournant.
L'utilisation du fichier "fres_001.fig" ( cf figure 4) permet d'expliquer aux élèves le lien
entre le vecteur tournant à la tension électrique sinusoïdale.
Le vecteur peut subir une rotation par un simple glisser-déplacer(1) du point M et sa
longueur peut également être modifiée en déplaçant le point A.
On atteint ainsi le premier objectif principal :
 Une tension électrique sinusoïdale peut être
modélisée par un vecteur-tournant.
(1) glisser-déplacer : revient à déplacer un objet par un clic gauche de souris. Ne pas lâcher le bouton
de la souris tant que l'objet n'est pas à la place désirée.
Figure 4 - fichier "fres_001.fig" sous cabri II géomètre

GRISP - Académie de Créteil - 2002
On atteint également un sous-objectif :
 - a - La longueur du vecteur correspond à la valeur de la tension
maximaleU; .
2) la pulsation  et la vitesse de rotation d'un
vecteur de Fresnel
L'utilisation du fichier "fres_002.fig" permet de comparer les courbes générées par
deux vecteurs-tournants dont les vitesses de rotation sont proportionnelles.
Le multiple (2 dans l'exemple ci-dessus, figure 5) peut être modifié pour explorer la
notion de pulsation d'un vecteur de Fresnel.
On atteint ainsi un second sous-objectif :
 - b- On appelle pulsation la vitesse de rotation du vecteur
et on la note . Elle a pour unité le radian par seconde
(rad.s-1) et influence directement l'aspect de la
courbe. On appelle période T, exprimée en seconde, le
temps mis par le vecteur pour faire un tour complet.
On appelle fréquence f, exprimé en Hertz, le nombre
de tour qu'a effectué le vecteur en une seconde.
Figure 5 - fichier "fres_002.fig" sous cabri II géomètre
Figure 6 - double, triple ou quadruple de la pulsation 1.