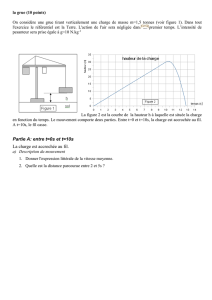
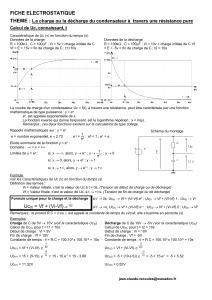
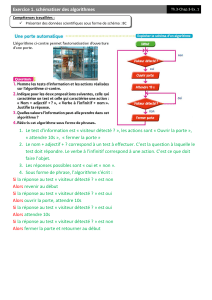
Telecharger ce cours (118 ko)

Remarque : la notion d'ordre est l'estimation d'une limite supérieure du temps
d'exécution d'un algorithme sur un exemplaire de taille donnée. L’estimation
d'une limite inférieure est donnée par :
Omega de f(n) : (Minoration)
Ω(f(n)) = {t : N -->IR / ( ∃ c ∈ IR+) ( ∃ n0 ∈ IN) (∀ n ≥ n0 ) [t(n) ≥ c f(n)]}
Exercice :
Soient f, g : N --> R+ , montrer que : f(n) ∈ O(g(n)) ⇒ g(n) ∈ Ω(f(n))
Ordre exact de f(n) : Te ta de f(n) :
Θ(f(n)) = O(f(n)) ∩ Ω(f(n))) ou encore : c1 f(n) t(n) c2 f(n)
t(n) est borné supérieurement et inférieurement par des multiples d’une même
fonction
Théorème :
Récurrences non homogènes
A) Récurrences de la forme: (R1)
a0 tn + a1 tn-1+ an-k tn-k = bn Pd (n) avec d le degré du polynôme P(n)
On déduit de (R1) l'équation caractéristique (EC1) qui suit :
( a0 xk-0 + a1 xk-1 +..+ ak x0) ( x - b )1+d = 0
Une combinaison linéaire des racines à la puissance n : rin de (EC1) et
de c0 bn constitue la forme explicite de tn , soit :
tn = c1 r1n + c2 r2n + ... + ck rkn + c0 bn ceci permet de déterminer l'ordre
Rq Si une racine r est de multiplicité m (=1+d) avec d≠0 alors sa contribution
dans l'expression de tn est : 0 n0 rn1 n1 rnm-1 nm-1 rn
B) Récurrences de la forme: (R2)

a0tn +...+ an-k tn-k= b1nPd1(n) + b2n Pd2(n) +..+bqn Pdq (n)
avec dj les degrés des polynôme P(n)
On déduit de (R2) l'équation caractéristique qui suit (EC2):
(a0 xk + a1 xk-1 + … + ak ) (x-b1)1+d1(x-b2)1+d2...(x-bq)1+dq = 0
Là aussi une combinaison linéaire des racines simples ri et des bi de
(EC2) à la puissance n : constitue la forme explicite de tn :
tn = Ʃ j rjn + k+1 b1n + k+2 b2n + ... + k+q bqn
avec rj les racines de la première parenthèse
l'ordre est obtenu à partir de cette forme de tn
Récurrences DPR
Théorème : Soient a, b, c et d ≥ 0 , n = bk et Les temps d'exécution
donnés par la récurrence:
d pour n = 1
T(n) = a T(n/b) + c n pour n > 1
alors l'Ordre de ces temps est :
O(n) si a < b
T(n) ∈ O(n logb n) si a = b
O(n logba) si a > b
T(n)=temps d'exécution d'un algorithme DPR pour l’exemplaire n
Rappel: a Ln b = b Ln a
Classification des ordres des temps les plus rapides aux plus lents
+ Rapide --> + lent
O (1) ⊂ O(Log n) ⊂ O(√n) ⊂ O(n) ⊂ O(n Log n) ⊂ O( n(1+x) ) ⊂
O( n(1+x) ) ⊂ O( n2/Log n )⊂ O(n 2) ⊂ O( (1+x)n )
Tours de Hanoï

procédure Hanoï (m,i,j)
si m > 0 alors
Hanoï (m-1,i,6-i-j)
écrire (i,"-->",j)
Hanoï (m-1,6-i-j,j)
Travail demandé
 Faire la trace de Hanoi (3, 1, 2)
 En déduire la relation de récurrence qui donne le temps d’exécution : t(m)
 Donnez alors l’ordre de ce temps
 Exprimez t(m) explicitement en fonction de m ; calculez ce temps pour m=64
Trace de Hanoi(3,1,2)
Hanoi(3,1,2)
Hanoi(2,1,3)
Hanoi(1,1,2)
Hanoi(0,1,3)
1-->2
Hanoi(0,3,2)
1-->3
Hanoi(1,2,3)
Hanoi(0,2,1)
2-->3
Hanoi(0,1,3)
1-->2
Hanoi(2,3,2)
Hanoi(1,3,1)
Hanoi(0,3,2)
3-->1
Hanoi(0,2,1)
3-->2
Hanoi(1,1,2)
Hanoi(0,1,3)
1-->2
Hanoi(0,3,2)
Diviser Pour Régner : DPR
C'est une technique de conception d'algorithmes consistant à décomposer l'exemplaire x à
résoudre en k sous exemplaires xi plus petits du même problème, à résoudre
successivement et indépendamment, puis à re combiner les sous solutions yi ainsi obtenues
pour parvenir à la solution de l'exemplaire de départ. De quelle manière résoudre les sous
exemplaires ?
Toute la puissance de la technique DPR réside dans la réponse à cette question.
Plan
1 Fouille dichotomique

2 Multiplication des grands entiers
3 Multiplication matricielle
4 Exponentiation discrète
Principe général de la technique DPR :
fonction DPR(x)
/* cette fonction retourne comme valeur la solution de l'exemplaire x */
si x est suffisamment petit alors retourner ADHOC(x) décomposer x en sous-exemplaires
plus simples: x1, x2,...,xk pour i <-- 1 jusqu'à k faire yi <-- DPR(xi) re combiner les yi pour
obtenir une solution y à x retourner y
où ADHOC , le sous algorithme de base , sert à résoudre les k petits exemplaires du
problème. Lorsque k=1 on ne parle pas de technique DPR mais d'algorithme de
simplification.
 1 Fouille
Il s'agit de retrouver un mot dans un dictionnaire ou un tableau. le pb consiste à
localiser un élément x dans le tableau T déjà trié en ordre croissant c.à.d. trouver i tel
que T[i] ≤ x < T[i+1] par les algorithmes suivants:
Travail demandé pour Mercredi 4 Mars :
Ecrire un algorithme séquentiel et un algorithme dichotomique et donnez leur ordre.
fonction fouille (T[1..n] , x)
/* recherche dichotomique de x dans T */
si n = 0 ou x < T[1] alors retourner 0
sinon retourner dichotorec(T , x)
fonction dichotorec(T[i .. j] , x)
/* recherche dichotomique de x dans le sous tableau T[i..j]
cette fonction n'est appelée que si i≤j et T[i] ≤ x < T[j+1] */
si i = j alors retourner i
k <-- (i+j+1) div 2
si x < T[k] alors retourner dichotorec(T[i...k-1] , x )
sinon retourner dichotorec(T[k...j] , x )
Trace et Ordre pour n = 8 x = 5 T = [ 1,4,5,8,11,14,20,23]
 2 Multiplication des grands entiers
Supposons que l’on veuille effectuer le produit u*v , mais quand la taille de u ou v dépasse la
longueur d'un mot machine la multiplication ne reste pas une opération élémentaire. Le
nombre de multiplications effectuées par le programme est un bon indicateur pour l'ordre.
Pour diminuer le temps: Décomposons u et v comportant n chiffres par une technique DPR:
on divise par 2 les nombres u et v, ainsi :
u = 10s w + x et v = 10s y + z ; s = n/2 d’où
u*v = 102s w.y + 10s (wz + yx) + x.z

Supposons que l’on veuille effectuer le produit u*v
Décomposons u et v ainsi
U = 10s w + x v = 10sy+z où 0<=x, z<10s et s= n/2
u*v= 102s wy + 10s (wz + yx) + xz
Fonction multA A(u, v: entiers): entier
n  max(taille u, taille v) /* taille = nombre de chiffres */
si n est petit alors multiplier u et v par l’algorithme
classique retourner le résultat
sinon s  n div 2
w  u div 10s , x  u mod 10s
y  v div 10s , z v mod 10s
retourner: mult(w,y)*102s + { mult(w,z) + mult(y,x) }*10s + mult(x,z)
Amélioration de la multiplication DPR
Fonction multB (u, v: entiers): entier
si n est petit alors multiplier u et v par l’algorithme
classique retourner le résultat
sinon s  n div 2
w  u div 10s x  u mod 10s
y  v div 10s z  v mod 10s
r  multB(w+x , y+z) p  multB(w,y) q  multB(x,z)
retourner 102s p + ( r - p - q )*10s + q
Exercice : Trace pour u = 1234 et v = 1321
Expliquez le résultat !
Montrer que t(n) ∈ O(n1,59)
Appliquez les algorithmes multA et multB à cette décomposition.Donnez les ordres de la
multiplication classique, et de multA et multB
Comparer l'ordre de mult et de la multiplication classique