Résumé du cours d`OPTIQUE

Résumé du cours d’OPTIQUE
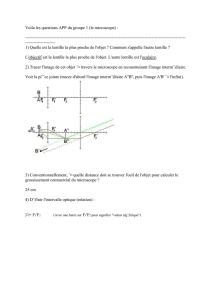
Qu’est-ce qu’une lentille ?
Un dioptre est la surface de séparation entre deux milieux (matériaux) transparents différents.
Une lentille est un milieu transparent limité par deux dioptres sphériques (l’un des deux dioptres peut être plan)
La lentille est convergente si elle est plus épaisse au centre que sur les bords (sinon elle est divergente).
Si on positionne une lentille convergente à proximité de cette feuille, on observe à travers elle le texte plus gros.
Dans le cas d’une lentille divergente le texte apparaît plus petit.
Une lentille est mince si son épaisseur au centre e est « petite » devant
les rayons de courbure (R et R’) de ses faces.
Le symbole d’une lentille mince convergente est :
Une lentille est caractérisée par :
* son centre optique O = le centre de symétrie de la lentille.
* son axe optique = axe perpendiculaire à la lentille et passant par O.
L’axe optique est orienté positivement dans le sens de propagation de la lumière.
* son foyer objet F et son foyer image F’, symétriques par rapport au centre optique O.
* sa distance focale f ’ = OF’ (mesure algébrique positive pour une lentille convergente) exprimée en m
ou sa vergence c =1/f ’. Son unité est la dioptrie de symbole  ( ou m–1).
* son plan focal objet = plan perpendiculaire à l’axe optique, passant par F.
* son plan focal image = plan perpendiculaire à l’axe optique, passant par F’.
Marche d’un rayon lumineux à travers une lentille mince convergente.
 Tout rayon incident passant par le centre optique O de la lentille n’est pas dévié.
 Tout rayon incident parallèle à l’axe optique
ressort de la lentille en passant par son foyer image F’.
 Tout rayon incident passant par le foyer objet F
ressort de la lentille parallèle à l’axe optique.
Objets et images :
Un point objet se trouve à l’intersection de plusieurs rayons lumineux incidents (arrivant vers la lentille).
Un objet est par définition un ensemble de points objets.
On symbolise un objet par une flèche (notée AB) ayant son origine sur l’axe
optique de la lentille et perpendiculaire à cet axe optique.
Remarque : le point objet B n’est pas forcément à l’origine des rayons incidents.
Il suffit qu’il soit à leur intersection, il n’a pas alors d’existence matérielle.
Il peut même être positionné après la lentille, sur le prolongement des rayons
incidents qui doivent alors apparaître en pointillés. Dans ce cas il est virtuel.
Si l’objet est avant la lentille, il est réel.
Défauts d’une lentille réelle :
Tous les rayons lumineux issus d’un point B qui rencontrent la lentille sont déviés
mais ne convergent pas tous vers le même point B’ !
Seuls les rayons incidents qui respectent les conditions de Gauss convergent approximativement au même point B’
appelé image du point B à travers la lentille.
Si l’image B’ est située après la lentille, elle est réelle. Si l’image est située avant la lentille, elle est virtuelle.
Conditions de Gauss:
 Les rayons incidents doivent être peu inclinés par rapport à l’axe optique.
 Ils doivent être peu écartés de l’axe optique et donc rencontrer la lentille près de son centre optique.
Dans ces conditions, on dit que les rayons incidents sont paraxiaux.
e
axe
optique
x
F
x
F’
x
O
L
>
Plan focal
image
x
F
x
F’
x
O
Plan focal
objet
x
F
x
F’
x
O
x
F
x
F’
x
O
B
A
B’
L
>
x
O
B
B’
L
>
x
x
x
F
x
F’
x
O
A
B
L
>
1

=
A’B’
AB
=
OA’
OA
Modèle de la lentille mince :
Un modèle est une représentation simplifiée et idéalisée de la réalité (on néglige certains défauts).
La lentille mince est une modélisation de la lentille réelle qui présente les deux propriétés suivantes :
 stigmatisme : tous les rayons lumineux incidents passant par un même point objet A traversent la lentille
et en ressortent en se coupant en un même point, appelé point image et noté A’.
 aplanétisme : l’image d’un objet plan AB perpendiculaire à l’axe optique est plane et perpendiculaire à
l’axe optique, notée A’B’.
Relation de conjugaison :
Elle permet de déterminer par le calcul la position de l’image
connaissant la position de l’objet et la distance focale de la lentille utilisée.
Grandissement de la lentille :
Attention ! Ces relations font intervenir des mesures algébriques qui ont un signe + ou – .
Si est négatif, l’image est renversée par rapport à l’objet. Si est négatif, l’image est droite.
Si est inférieur à 1, l’image est plus petite que l’objet.
Exemple : En supposant que le point objet A soit situé 20,0cm avant la lentille et que son image A’ se trouve
30,0cm après la lentille, déterminer la distance focale de la lentille ainsi que sa vergence C .
Attention aux signes ! OA = – 0,200m OA’= + 0,300m relation de conjugaison :
'
1
OA
=
OA
1
+
'
1
OF
Donc C = 1 / OF’ = (1/0,300) – (1/–0,200) = (2/0,600) + (3/0,600) = 5/0,600 = 8,33   OF’= 0,600/5 = 0,120m
Calculer le grandissement dans ce cas : = OB’/ OB = 0,300 /(–0,200) = –1,50
Quelles sont les caractéristiques de l’image A’B’? OA’ > 0 donc l’image est réelle car située après la lentille
(donc sur les rayons émergeants de la lentille et non pas sur leurs prolongements avant la lentille).
D’autre part cette image est renversée car  est négatif , et plus grande que l’objet car   1.
Objet situé à l’infini :
Tous les rayons incidents provenant d’un point objet A situé à l’infini sur
l’axe optique de la lentille sont parallèles à l’axe optique.
Ils sont déviés par la lentille et convergent au foyer image F’.
Tous les rayons incidents provenant d’un point objet B situé à l’infini en
dehors de l’axe optique de la lentille sont parallèles entre eux.
Ils sont déviés par la lentille et convergent en un point B’ du plan focal image.
Ce point est déterminé grâce au rayon incident qui passe par O et n’est pas dévié.
Si l’objet est situé à l’infini, son image se trouve dans le plan focal image de la lentille.
Méthode pour tracer la marche d’un rayon incident quelconque :
 Tracer en pointillé un rayon incident fictif parallèle à celui qui nous intéresse
et passant par O : il traverse donc la lentille sans être dévié.
 Le rayon incident qui nous intéresse est dévié par la lentille de façon à couper
le rayon fictif dans le plan focal image de la lentille.
Image résultante à l’infini :
Si l’objet est situé dans le plan focal objet de la lentille, son image se trouve à l’infini
Grandissement ou grossissement ?
Si l’objet AB ou son image A’B’ sont rejetés à l’infini, leur taille n’est pas définie (elle est infinie !) donc le
grandissement de la lentille ne peut être calculé. On définit alors son grossissement G (voir la loupe page 3).
1
OA’
1
OA
1
OF’
=
+
B’
A
A’
B
F’
O
L
>
x
F
x
F’
x
O
Plan focal
image
x
F
x
F’
x
O
L
>
 A
A’
x
F
x
F’
x
O
L
>
B’
B
Plan
focal image
x
x
F
x
F’
x
O
L
>
B
B’
Plan
focal objet
x
2

Instruments d’optique
L’œil modélisé :
L’œil est constitué par une lentille convergente (appelée cristallin) dont le rôle est de
former une image nette de l’objet observé sur la rétine, qui peut être assimilée à un écran.
La pupille est un diaphragme de diamètre variable qui régule la quantité de lumière qui pénètre dans l’œil.
Comment l’œil accommode-t-il ? La distance focale du cristallin est variable, grâce à l’action
de muscles qui sont au repos lorsque l’œil observe un objet situé à l’infini (punctum remotum).
La distance minimale de vision distincte, appelée punctum proximum, est de 25cm.
Comment trouver l’image B’ d’un objet B sur la rétine ? Tracer le rayon issu de B et passant par le centre
optique O… il n’est pas dévié et rencontre la rétine au point image B’ (voir ci-dessous).
diamètre apparent d’un objet AB observé à l’œil nu
C’est l’angle  sous lequel cet objet est observé à partir du
centre optique O de l’œil lorsque l’objet est au plus proche
de l’œil, soit 0,25m (punctum proximum)
Rappel : Pour un angle « petit » on peut assimiler le sinus, la tangente et la valeur de l’angle
exprimée en radian. Donc  = AB / OA = AB / 0,25 = 4,0 x AB
Défauts de l’œil : * myopie : la distance cristallin-rétine est trop grande  correction = lentille divergente
* hypermétropie : la distance cristallin-rétine est trop petite  correction = lentille convergente
Généralités sur les instruments d’optique :
Lorsqu’un instrument d’optique est constitué par plusieurs lentilles, la première lentille L1 rencontrée par la
lumière provenant de l’objet observé s’appelle objectif .
L’objectif donne de cet objet AB une image intermédiaire A1B1 qui doit être déterminée graphiquement
comme si les autres constituants de l’instrument (lentilles, miroirs,…) n’existaient pas.
A1B1 joue alors le rôle d’objet pour la deuxième lentille L2 … et ainsi de suite.
La dernière lentille rencontrée par la lumière avant de pénétrer dans l’œil de l’observateur est l’oculaire.
Tous les instruments d’optique sont réglés de façon à ce que l’image résultante soit rejetée à l’infini.
Ainsi, l’œil de l’observateur n’a pas à accommoder et les muscles ciliaires ne fatiguent pas.
Utilisation du banc d’optique :
Intérêt : le banc d’optique sert de support aux différents composants d’un montage, il permet d’aligner leurs
axes optiques et d’effectuer des mesures de distances entre ces composants.
Réalisation d’un « objet » : une feuille de papier calque est plaquée contre une plaque opaque percée d’un
trou dissymétrique (en forme de 1 ou de i) et est éclairé par une lampe.
L’objet est le calque qui diffuse dans toutes les directions la lumière de la lampe.
On peut augmenter la quantité de lumière émise par cet objet en intercalant entre la
lampe et le trou un condenseur constitué par une ou deux lentilles très convergentes.
La loupe :
C’est une lentille convergente de courte distance focale,
de vergence C , qui donne d’un objet réel AB une image
A1B1 située à l’infini.
L’objet doit donc être situé dans le plan focal objet de la loupe.
Cette image intermédiaire A1B1 joue le rôle d’objet pour l’œil.
L’œil voit A1B1 sous un angle 1 supérieur à .
Grossissement standard de la loupe : G = 1/ = C/4
En effet : θ = AB / 0,25 = 4,0xAB et θ1 = AB / f ’ = CxAB  Une loupe de distance focale 2,5cm grossit 10 fois
O
 = 4,0 x AB
B
B’
A
A’
O
25cm
1,5cm
B’
A’
x
F’
x
O
L
>
B
B1
Plan
focal objet
A
A1
θ1
f’
loupe
œil modélisé
L
>
B
A
θ
0,25m
Punctum proximum
3
objet
A
condenseur
lampe

La lunette astronomique :
L’objectif L1 donne de l’objet AB situé à l’infini une image réelle A1B1 qui se forme dans son plan focal image.
L’oculaire L2 joue le rôle de loupe pour grossir A1B1 et en donne une image résultante A2B2 à l’infini.
Pour cela, A1B1 doit être dans le plan focal objet de l’oculaire L2 .
La lunette est un instrument afocal car elle donne d’un objet à l’infini une image située à l’infini.
La mise au point s’effectue en modifiant la distance entre l’objectif et l’oculaire.
A1 est confondu avec le foyer image F’1 de L1 et le foyer objet F2 de L2
Attention ! pour cet instrument, l’objet ne peut pas être placé au punctum proximum car il est à l’infini !
Donc θ est l’angle sous lequel l’observateur observerait l’objet AB à l’œil nu. On constate que θ = A1B1/ f’1
Et θ2 est l’angle sous lequel l’observateur observe l’image résultante A2B2 à travers l’oculaire  θ2 = A1B1/ f’2
Grossissement de la lunette : G = θ2 / θ = f’1 / f’2  changer d’oculaire pour modifier le grossissement.
Le cercle oculaire est par définition l’image de l’objectif (considéré comme objet) à travers l’oculaire.
Relation de conjugaison :
A.N. avec f1’ = 1,000m et f2’ = 1,0cm
O2O1 = –1,010m et OF2 = +0,010m
Le calcul (à faire !) conduit à O2C = 0,0101  0,010m  le cercle oculaire est très proche du plan focal image
de l’oculaire. C’est dans cette zone qu’il faut placer l’œil pour capter un maximum de lumière.
Le microscope :
L’objectif L1 donne de l’objet AB situé à proximité de son plan focal objet une image réelle A1B1 agrandie.
L’oculaire L2 joue le rôle de loupe pour grossir A1B1 et en donne une image résultante A2B2 à l’infini.
Pour cela, A1B1 doit être dans le plan focal objet de l’oculaire L2 .
La mise au point s’effectue en modifiant la distance entre l’objet observé et le microscope.
Remarque : l’objet AB est en réalité beaucoup plus proche du plan focal objet de l’objectif … ce qui conduit à
une image intermédiaire A1B1 beaucoup plus grande que sur le schéma ci-dessus qui n’est pas à l’échelle.
Grandissement de l’objectif L1 : en valeur absolue
Grossissement de l’oculaire L2 : G2 = 2 / 1 = = = 4,0 x f’2
Grossissement du microscope : G = 2 /  = = x G2
On modifie le grossissement du microscope en changeant d’objectif : si f’1 varie, varie aussi.
Attention ! l’objet est AB pour le microscope mais A1B1 pour l’oculaire… donc  ≠ 1 .
B’
A’
x
F’2
x
O2
L
>
B1
B2
Plan
focal
A1
A2
θ2
f’2
oculaire L2
œil modélisé
f’1
x
O1
objectif L1
θ
B
A
x
F’2
x
O2
oculaire L2
x
O1
objectif L1
x
F’1= F2
Cercle
oculaire
C
1
O2C
1
O2O1
1
OF2
=
+
’
’
B’
A’
x
F’2
x
O2
L
>
B1
B2
Plan
focal objet
A1
A2
θ2
f’2
oculaire L2
œil modélisé
f’1
x
O1
objectif L1
A
B
x
F1
x
F’1
 = intervalle optique
Plan
focal objet
A1B1/ f’2
A1B1/ 0,25
A1B1/ f’2
AB / 0,25
1
=
A1B1
AB
=
O1A1
O1A
=
 + f’1
O1A
f’2
0,25
1
1
4

C x
R
S
x
F
x
C
x
F
x
S
x
C
x
F
x
S
x
B
Plan
focal
B’
∞
Les miroirs :
Le miroir plan :
Le miroir plan est stigmatique : il donne d’un point objet A une image
ponctuelle A’ qui est symétrique de A par rapport au miroir.
Si l’objet est réel (à l’intersection des rayons incidents, avant le miroir), son
image est virtuelle (derrière le miroir, sur le prolongement des rayons réfléchis).
Si l’objet est virtuel (derrière le miroir, sur le prolongement des rayons incidents),
son image est réelle (à l’intersection des rayons réfléchis, devant le miroir).
Méthode pour tracer un rayon réfléchi :
* le point objet A est connu, sinon prendre un point A sur le rayon incident.
* placer A’, symétrique de A par rapport au miroir plan
* noter I le point d’incidence (où le rayon incident rencontre le miroir)
* le rayon réfléchi passe par A’ et I
il faut tracer en pointillé tout ce qui est virtuel, derrière le miroir.
Le miroir sphérique :
Il est formé d’une portion de sphère (de centre C et de rayon R)
dont la face concave (creuse) est réfléchissante.
R est appelé rayon de courbure du miroir, C son centre de courbure.
L’axe optique principal passe par le centre C et par le sommet S du miroir.
On l’oriente dans le sens de propagation de la lumière incidente.
On admettra que, dans les conditions de Gauss, le miroir convergent est stigmatique (l’image d’un objet
ponctuel est ponctuelle) et aplanétique (l’image d’un objet plan perpendiculaire à l’axe optique est plane et
perpendiculaire à l’axe optique).
La distance focale du miroir convergent est égale à la moitié de son rayon de courbure : f ’ = R/2
Le foyer objet et le foyer image sont confondus au centre F du segment CS.
On symbolise un miroir sphérique concave par un trait, aux extrémités
duquel on ajoute deux tirets, représentant sa concavité :
 Tout rayon incident passant par le centre C du miroir n’est pas dévié
Il est donc réfléchi sur lui-même
 Tout rayon incident passant par le foyer F du miroir
est réfléchi parallèlement à l’axe optique
 Tout rayon incident parallèle à l’axe optique du miroir
est réfléchi en passant par le foyer F
Cas d’un objet à l’infini :
Si le point objet A est sur l’axe optique, tous les rayons provenant de A sont
parallèles à l’axe optique et convergent au foyer F  image A’ en F.
Si le point objet B n’est pas sur l’axe optique, son image B’ se trouve dans le plan focal du miroir.
On détermine B’ en traçant le rayon issu de B (donc parallèle au rayon incident donné sur le schéma) et passant
par le foyer F : il est réfléchi parallèlement à l’axe optique et rencontre le plan focal au point B’ cherché.
Le télescope de Newton : voir animations sur le site www.physiquepovo.com
Le miroir primaire sphérique donne de l’objet AB situé à l’infini une image réelle A1B1 qui se forme dans son
plan focal. Plus son diamètre est grand, plus il capte de lumière et permet d’observer des étoiles éloignées.
Le miroir secondaire plan donne une image A2B2 symétrique de A1B1 par rapport à ce miroir.
L’oculaire L2 joue le rôle de loupe pour grossir A2B2 et en donne une image résultante A3B3 à l’infini.
xA
A’x
Image virtuelle
objet réel
I
xA’
Ax
objet virtuel
image réelle
I
L
>
5