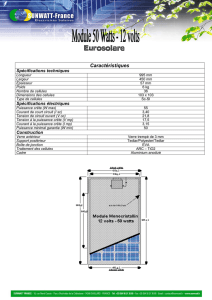
Nom - Physique Appliquée

Nom
Montages intégrateurs et dérivateurs
Classe Gr :
Date
TP n°:
Objectifs :  Fonctionnements linéaire d'un montage à amplificateur opérationnel.
 Savoir définir la fonction d'un montage amplificateur.
 Appliquer les lois de l'électricité pour déterminer une relation entre grandeur d'entrée et
grandeur de sortie dans des montages simple amplificateur
 Etude des filtres utilisés dans les asservissements
 Utilisation des diagrammes
Pré requis  Amplificateur opérationnel
 Les complexes
Conditions de réalisation :  Les consignes de tension ou de courant sont données dans l’énoncé
 Mettre l’amplificateur opérationnel sous tension en priorité.
TRAVAIL DEMANDE :
I.1) Rappeler les propriétés de l’AO parfait .
II) Montages intégrateurs
II.1) Etude théorique
II.1.1) Montage théorique : l’intégrateur pur
On considère les montages suivants, pour lesquels R = 10 k, C = 0,1 µF, Uecc (tension crête à crête) = 2 V.
u
s
C
u
e R
Etablir la relation :
dtu
RC
ues   1
(l’A.O. est supposé idéal, en régime linéaire).
En déduire us(t) pour une tension ue rectangulaire symétrique. L'étude sera limitée à l'intervalle 0 t T/2, et on
précisera les valeurs maximale et minimale de us à la fréquence f = 1000 Hz; d'où la tension Uscc (tension crête à crête).
Retrouver l’expression de la transmittance
1
s
e
u
Tu jRC
Tracer les diagrammes de Bode, Black et Nyquist correspondants.
II.1.2) Le montage d'étude
Etablir la fonction de transfert du montage sous la forme :
1
c
A
Tj
avec
0
R
AR
et
0
1
cRC
Mettre en évidence le comportement intégrateur au-delà d’une fréquence de coupure que l’on précisera
R
u
e
u
s
C
R
o
log
f
log
f
c
G(dB) = 20logT
a)
b)
pente
-20dB/décade
10 k
100 k
0,1 µF
iintégrateur
Amplification limitée
II.2) Manipulation
ue est une tension carrée symétrique d’amplitude 1 V et de fréquence 1000 Hz.
II.2.1) Observer la dérive du signal de sortie, à la mise sous tension du circuit, en l'absence de R0..
II.2.2) R0 étant en place, relever l'oscillogramme et observer le comportement intégrateur pour divers signaux
Mesurer la composante continue de la tension us.
En déduire la tension d'offset responsable de ce décalage.
II.2.3) La tension ue est maintenant une tension sinusoïdale d’amplitude 2 V et de fréquence variant de fc/100 à 100fc

Remplir le tableau suivant et tracer les diagrammes correspondants
On pose : Arg T =  ; Re = T  x cos  ; Im = T  x sin  ; GdB = 20 log T .
0
C
100
3
C
100
C
10
3
C
10
c
3 c
10 c
30 c
100 c
f en Hz
uS
T 
Re
Im
II.3) Etudes connexes
II.3.1) Le filtre passe bas
On considère les montages suivants, pour lesquels R = 10 k, C = 0,1 µF
R
C
ue
us
Retrouver l’expression de la transmittance complexe :
1
()
1
c
Tj j
on posera
1
cc
X
RC
et
Remplir le tableau suivant :
Tracer les diagrammes de Bode, Black et Nyquist correspondants
On pose : Arg T =  ; Re = T  x cos  ; Im = T  x sin  ; GdB = 20 log T .
0
C
100
3
C
100
C
10
3
C
10
c
3 c
10 c
30 c
100 c
f en Hz
T 
GdB
Re
Im
Remarquer le comportement en intégrateur au-delà d’une fréquence de l’on précisera

III) Montages dérivateurs
III.1) Etude théorique
III.1.1) Montage théorique : le dérivateur pur
On considère les montages suivants, pour lesquels R = 10 k, C = 0,1 µF, Uecc = 2 V .
Etablir la relation :
e
sdu
u RC dt
(dans l'hypothèse de l'A.O. idéal, en régime linéaire)
R
u
e
u
s
C
S
En déduire us(t) pour une tension ue triangulaire symétrique. On précisera les valeurs maximale et minimale de us à la
fréquence f = 1000 Hz, d'où la tension crête à crête Uscc.
Retrouver l’expression de la transmittance
s
e
u
T jRC
u
Tracer les diagrammes de Bode, Black et Nyquist correspondants.
Inconvénients de ce montage
L'AO , pris isolément, se comporte comme un filtre passe-bas de fréquence de coupure fo de valeur très faible ( de l'ordre de
10 Hz ), donc comme un intégrateur pour les fréquences supérieures à 10 Hz. Par ailleurs, pour les fréquences moyennes, le
montage est instable: il apparaît des oscillations. Pour les éviter, il faut limiter le gain du montage, par la mise en place d'un
résistor R1 en série avec le condensateur.
III.1.2) Le montage d'étude
R
u
e
u
s
C
S
R
1
G(dB) = 20 logT
pente :
20 dB/décade
pente :
20 dB/décade
logf
dérive
amplifie
intègre
R1 : boites à décade x10 ; x100 .
Application: on montre que la pente de + 20 dB/ décade correspond à un fonctionnement en dérivateur. Reconnaître sur le graphe
ci-dessus, les parties où sont réalisées l'intégration, l'amplification, et la dérivation.
Exprimer l’amplification en tension du montage pour une tension d'entrée continue :
Etablir la fonction de transfert du montage sous la forme :
0
1
1
j
Tj
avec
01
RC
et
11
1
RC
Mettre en évidence le comportement dérivateur autour d’une fréquence de coupure que l’on précisera
Tracer les diagrammes de Bode, Black et Nyquist correspondants.
On pose : Arg T =  ; Re = T  x cos  ; Im = T  x sin  ; GdB = 20 log T .
0
C
100
3
C
100
C
10
3
C
10
c
3 c
10 c
30 c
100 c
f en Hz
T 
GdB
Re
Im

III.2) Manipulation
ue est une tension triangulaire symétrique d’amplitude 1V et de fréquence f = 1000Hz.
– Observer l'influence de R1. Pour quelle valeur de R1, les oscillations sont-elles supprimées?
– Relever Uscc. Comparer Uscc à la valeur théorique calculée.
– Relever l'oscillogramme.
III.3) Etudes connexes
III.3.1) Le filtre passe haut
On considère les montages suivants, pour lesquels R = 10 k, C = 0,1 µF
R
C
ue
us
Retrouver l’expression de la transmittance complexe :
()
1
C
C
j
Tj j
: on posera
1
cc
X
RC
et
Remplir le tableau suivant :
Tracer les diagrammes de Bode, Black et Nyquist correspondants.
On pose : Arg T =  ; Re = T  x cos  ; Im = T  x sin  ; GdB = 20 log T .
0
C
100
3
C
100
C
10
3
C
10
c
3 c
10 c
30 c
100 c
f en Hz
T 
GdB
Re
Im
Remarquer le comportement en dérivateur au-delà d’une fréquence de l’on précisera
IV) Filtre PID
Déterminer pour les deux filtres les transmittances et tracer les diagrammes correspondants.
C1
R1
R2
v2
v1
R1R2
C2
v2
v1
1
( ) 1T j A j
2
1
1
1
)(
j
j
jT