POUSSÉE D`ARCHIMÈDE

PhG-Sciences
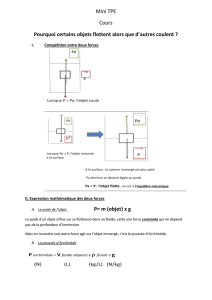
POUSSÉE D’ARCHIMÈDE
L'eau et l'air exercent aussi des forces et modifient la vitesse d'un objet !
«… currens identidem graece clamabat EYPHKA EYPHKA. »
« En courant il criait sans cesse en grec : EUREKA ! EUREKA ! » Archimède 287-212 av. JC
Poussée d'Archimède
Un corps immergé dans un fluide (liquide ou gaz) subit de la part du fluide des forces dont la
résultante est verticale vers le haut et d’intensité égale au poids du volume de fluide déplacé.
Autre énoncé
Tout corps plongé dans un liquide (ou un gaz) reçoit une poussée verticale, qui s'exerce de bas en haut, égale au
poids du volume de liquide (ou de gaz) déplacé.
Détermination du poids du fluide déplacé
Un corps de volume V est plongé dans un fluide de masse volumique .
Masse du fluide déplacé : m =  V
Poids de cette masse : P = m g
d’où : P =  V g
Intensité de la poussée d’Archimède
« L’intensité de la poussée d’Archimède est égale au poids du volume de fluide déplacé. »
PA = P d’où PA =  V g
Les caractéristiques de la poussée d’Archimède PA sont donc :
- direction : la verticale
- sens : de bas en haut
- intensité : PA =  V g.
- point d’application : le centre de poussée C
(centre de la partie immergée pour les corps homogène)
Remarque1 : c’est une force de contact réparti.
Remarque2 : elle se mesure indirectement à l’aide d’un dynamomètre (c’est une force).
PA = Phors du fluide - Pimmergé
La poussée d'Archimède est la force exercée sur tout corps immergé dans un fluide comme l'eau. C'est
ainsi qu'un navire flotte sur la mer. La poussée d'Archimède dans l'air est 755 fois plus faible que celle
dans l'eau. Elle est souvent négligée dans les études des forces par rapport au poids. Pourtant elle a
cependant des effets observables ; c'est elle qui explique pourquoi un ballon gonflé à l'hélium peut
s'envoler.
V
Fluide de masse volumique 
A
P
C

PhG-Sciences
POUSSÉE D’ARCHIMÈDE
Exercice 1 Solide suspendu à un ressort
Un solide S de masse m est accroché à un ressort de constante de raideur k.
A l’équilibre le ressort s’allonge d’une longueur x1.
Un becher contenant de l’eau à une masse m1.
Le solide S est plongé dans l’eau du becher.
Un nouvel équilibre est observé.
L’allongement du ressort devient égal à x2 et la masse
de l’ensemble est m2.
1- Établir l’expression de l’allongement x1 en fonction de m, g et k.
2- Établir l’expression de l’allongement x2 en fonction de m, me, g et k. Comparer à x1.
3- Exprimer la différence de pesée m2 – m1 (on considère le système {eau, becher}).
Rappel : l’intensité de la tension d’un ressort a pour expression F = k x.
Exercice 2 Iceberg
Un iceberg a un volume émergé Ve = 600 m 3. La masse volumique de l’iceberg est 1 = 910 kg m – 3 et
celle de l’eau de mer est 2 = 1024 kg m – 3.
1- Schématiser l’iceberg flottant et tracer les forces auxquelles il est soumis à l’équilibre.
2- Déterminer une relation entre le volume émergé Ve, le volume totale Vt et les masses volumiques.
3- Calculer le volume Vt et la masse m de l’iceberg
Exercice 3 Poids apparent
Une sphère de cuivre de 24,5 N est plongée dans un liquide de masse volumique 0,800 g/cm 3.
Le cuivre a une masse volumique de 8,00 g/cm 3.
On prendra g 9,81 N/kg.
Calculer le poids apparent de la sphère de cuivre (le poids apparent est le poids réel moins la poussée
d’Archimède).
Exercice 4 Gouttelette de brouillard
Une gouttelette de brouillard tombe dans l’air sans vent. L’air exerce sur la gouttelette, supposée
sphérique, une résistance dont la valeur est donnée par la formule de Stokes :
F = 6   R v où  = 1,8 10 – 5 SI est la viscosité de l’air, R est le rayon de la sphère et v
la vitesse de la gouttelette par rapport à l’air.
L’étude expérimentale montre que la gouttelette atteint une vitesse limite de 0,12 mm s – 1.
1- Schématiser les forces appliquées à la gouttelette.

PhG-Sciences
2- Établir la relation entre les intensités des trois forces appliquées à la gouttelette lorsque la vitesse
limite est atteinte.
3- En déduire le rayon R de la gouttelette.
4- Calculer la valeur PA de la poussée d’Archimède sur la gouttelette.
5- Comparer cette valeur à celle du poids de la gouttelette.
Exercice 5 Densité
Une sphère de laiton a dans l'air une masse de 160g. On l'immerge dans l'eau et elle parait ne plus
peser que 100g. La densité du laiton est 8.
1- La boule est-elle pleine ou creuse ?
2- Si elle est creuse, quel est le volume de la cavité intérieure ?
Exercice 6 Hiéron et Archimède
Le roi Hiéron, tyran de Syracuse, voulant offrir une couronne d'or à Jupiter, soupçonna l'orfèvre de
l'avoir faite en alliage d'argent et d’or.
C'est en cherchant à résoudre ce problème, sans détériorer la couronne, qu'Archimède découvrit la
poussée à laquelle on a donné son nom.
Dans l'air, la couronne pèse 41,8N et dans l'eau son poids apparent n'est plus que de 39,6N.
La densité de l'or est de 19,5 et celle de l'argent de 10,5.
1- Quelle est la densité du métal de la couronne ?
2- Quelle est la composition du métal de la couronne en masse et en volume ?
Quelques questions
Pour un apprenti nageur : Est-il plus facile de flotter en rivière ou en mer ?
Flotte-t-on mieux les bras hors ou dans l’eau ?

PhG-Sciences
Le saviez-vous ?
POUSSÉE D’ARCHIMÈDE
Ligne de charge – Load Lines
Il est important de remarquer que la poussée d'Archimède varie en fonction de la densité de l'eau.
L'eau douce est moins dense que l'eau de mer qui est riche en éléments minéraux comme le sel.
Un bateau ne pourra pas être aussi chargé dans l'eau douce que dans l'eau salée, car il faut déplacer
plus d'eau douce pour obtenir la même poussée d'Archimède. En eau douce, un navire sera donc plus
immergé à poids égal. Voilà pourquoi des règles internationales imposent aux bateaux d'avoir des
niveaux de flottaison clairement indiqués sur les côtés du bateau.
http://www.vialang.com/en/misc/illustr_gloss/ships/conn_parts.htm
Lignes de flottaison en charge peinte sur le côté du navire et indiquant la profondeur maximale à
laquelle un navire peut être enfoncé. Aussi appelée (rare) Ligne de Plimsoll, d'après le député
britannique qui les introduisit à la fin du XIX Siècle.