Interaction électrique

Exercices - physique 3ème année Maths Sc.Exp et Tech
http://cherchari.org/ - 1 - Cherchari
2
9.10.9 OMIqI
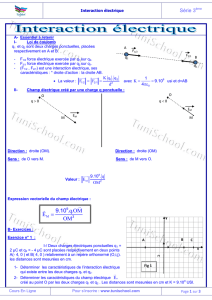
Loi de Coulomb - Le champ électrique
A- Essentiel à retenir
I- Loi de coulomb
q1 et q2 sont deux charges ponctuelles, placées
respectivement en A et B.
- F1/2 force électrique exercée par q1 sur q2.
- F2/1 force électrique exercée par q2 sur q1.
- (F1/2 , F2/1) est une interaction électrique, ses
caractéristiques : * droite d’action : la droite AB.
 La valeur : IIF1/2 II = IIF2/1II =
Error!
avec k =
Error!
=9.109 usi et d=AB
II- Champ électrique créé par une charge q ponctuelle :
Direction : droite (OM). Direction : droite (OM)
Sens : de O vers M. Sens : de M vers O.
Valeur : II EMII = Valeur : II EMII =
Expression vectorielle du champ électrique :
B- Exercices :
Exercice n° 1 :
I-/ Deux charges électriques ponctuelles
q1 = 2 µC et q2 = - 4 µC sont placées respectivement en deux
points A(- 4, 0 ) et B( 4, 0 ) relativement à un repère
orthonormé (O,i,j). les distances sont mesurées en cm.
1- Déterminer les caractéristiques de l’interaction
électrique qui existe entre les deux charges q1 et q2.
Déterminer les caractéristiques du champ électrique créé au
point O par les deux charges q1 et q2 . Les distances sont
mesurées en cm et K = 9.109 USI.
Déterminer les caractéristiques du champ électrique créé
au point C( 6, 0) par les deux charges q1 et q2.
2- Préciser, en le justifiant, en quel point de la droite AB
faut-il placer une troisième charge électrique q non nulle
pour qu’elle reste immobile.
3- La charge q2= - 2µC, déterminer les caractéristiques du champ électrique créé au point D( 0,
3) par les deux charges q1 et q2.
Exercice 2
Une tige isolante AB (AB = 20 cm ) est inclinée d’un angle  = 30° avec l’horizontale.
1- On fixe en A une charge q1 = - 10 nC, en B une charge q2 = 10 nC. Déterminer les
caractéristiques du vecteur champ électrostatique au point C situé sur la tige AB à 5 cm de A.
EO
EC
Fig 1
A
B
O
C
y
x
q  0
EM
M
O
q  0
EM
M
O
2
9.10.9 OMIqI
3
9..10.9 OM MOIqI
EM
q2
q1
F1/2
F2/1
A
B
ED

Exercices - physique 3ème année Maths Sc.Exp et Tech
http://cherchari.org/ - 2 - Cherchari
2- Une petite sphère (S) portant une charge q = 30 nC, de masse m, peut coulisser sans frottement
sur la tige AB, elle s’immobilise en C.
a- Faire le bilan des forces qui s’exercent sur la sphère (S) ; les
représenter.
b- En appliquant la condition d’équilibre de la sphère, calculer
la masse m et la valeur de la réaction de la tige.
On donne IIgII = 10 N.Kg-1.
3- En maintenant la tige AB horizontalement, la sphère reste t-
elle immobile ? si non dans quel sens va-t-elle se déplacer ?
Exercice n ° 3 :
Deux charges électriques ponctuelles q1 = 2
c
et q2 = - 2
c
sont placées respectivement en deux
points A et B tel que AB = 20 cm .
1°) Représenter le spectre crée par ces deux charges.
2°) a – Déterminer les caractéristiques du vecteur champ électrique crée par ces deux charges au
point C tel que
2AC AB
.
b – On place en C une troisième charge ponctuelle q=4
c
.
Déterminer les caractéristiques de la force électrique
F
exercée sur cette charge .
3° ) On supprime le charge q .
Déterminer les valeurs du champ électrique créé par les deux charges en un point N située sur la
médiatrice de AB tel que BI = 10 cm avec I=A*B .
Exercice n° 4
On place aux points A et B deux boules métalliques identiques
(B1) et (B2) supposées ponctuelles. La distance entre A et B est
égale à 2a. La boule (B1) porte la charge -q et la boule (B2)
porte la charge +q ( q>0). On note O milieu du segment [AB]
et () la médiatrice de [AB] contenue dans le plan de la figure.
Soit M un point de () distant de h du point O.(figure 1)
1-a- Définir la ligne de champ. Représenter le spectre électrique
des deux charges placées en A et B.
b- Représenter les vecteurs champs électriques ;EA et ;EB
créés respectivement par B1 et B2 au point M.
c-Exprimer la valeur de ;EA et de ;EB en fonction de K, q, a et h. Montrer que |; |;EA|; | =|; |;EB|; |.
K=9.109 u.s.i
2- On notera ;EM le champ électrique créé par les deux boules (B1) et (B2) au point M.
a- Déterminer les coordonnées EMx et EMy du vecteur ;EM dans le repère orthonormé (M,;i ,;j) en
fonction de K, q, a et h.
b- Montrer que ;EM = -
Error!
.
Error!
, avec cos =
Error!
.
c- Déduire la valeur de ;EM au point O. On donne a=10 cm, h=17,33 cm et q=0,3 µC.
3- On veut déterminer les caractéristiques de ;EM par construction géométrique, pour cela on donne
l’échelle suivante : 2.104 N.C-1
Error!
1 cm.
a- Représenter, à l’échelle, ;EA et ;EB au point M puis construire ;EM.
A
B
C
q1
q2
q
A
B
-q
+q
O
h
a
Fig 1
M
;i
;j

Exercices - physique 3ème année Maths Sc.Exp et Tech
http://cherchari.org/ - 3 - Cherchari
Déduire à partir de la construction géométrique les caractéristiques de ;EM.