Âge en Ma

OBJECTIFS : UTILISER LE LOGICIEL SISMOLOG, REALISER UN COMPTE-RENDU A PARTIR DES INFORMATIONS APPORTEES PAR LE LOGICIEL, EXPLOITER
DES CALCULS DE DENSITE
Problème 1 : Quelles sont les caractéristiques des zones de subduction ?
I. Morphologie, topographie et dynamisme d’une zone de subduction : La cordillère des Andes
 Ouvrir SISMOLOG.
 Faire apparaître le quadrillage.
 Positionner le curseur sur -22° de latitude et -72° de longitude.
 Aller dans le menu « Affichage », sélectionner « contour » puis cliquer sur « plaques » ; la
frontière entre les plaques lithosphériques apparaît.
 Zoomer trois fois de suite.
 Cliquer sur l’icône « relief 3D ». Une vue en 3D permet de visualiser la zone étudiée. Vous
pouvez modifier l’image à l’aide des touches F1, F2, F3 et du curseur…
 Faire apparaître les volcans en cliquant sur F2.
1. À partir du bloc diagramme à l’écran, décrivez le relief négatif et positif (indiquez les altitudes et
les profondeurs en vous servant de la fiche d’utilisation de Sismolog), Décrivez la localisation des
volcans.
 Sortir du relief 3D en appuyant sur la touche « echap ».
 Aller dans le menu « séismes » ; sélectionner « profondeur » puis cliquer sur « superficiel »,
Sélectionner ensuite « dessiner les séismes ». Chaque point jaune représente un séisme
superficiel (inférieur à 60 km).
2. Décrivez l’abondance des séismes et leur distribution.
 Faire apparaître les séismes de profondeur intermédiaire (entre 60 et 300 km) puis les
séismes profonds (supérieur à 300 jusqu’à 700 km).
3. Concluez sur l’évolution de la profondeur moyenne des foyers sismiques quand on s’écarte de la
fosse vers le continent.
 Aller dans le menu « outils », sélectionner « coupe » puis « définir ». Deux pastilles bleues
(1 et 2) apparaissent à l’écran. Attraper les pastilles bleues et les déplacer afin que la
pastille 1 soit à -28,3 de latitude et -73 de longitude et que la pastille 2 soit à -28,3 de
latitude et -62 de longitude.
 Aller dans le menu « outils », sélectionner « coupe » puis « dessiner ». La coupe apparaît à
l’écran. La case à cocher échelle 1:1 permet de recadrer la fenêtre automatiquement pour
que l'échelle en x et celle en y soit la même.
4. Vous constatez que les séismes s’alignent suivant une droite ou plan appelé Plan de Bénioff. Que
représente ce plan ? Vous indiquerez les plaques lithosphériques (lithosphère océanique ou
continentale) mises en jeu dans cette zone de subduction et leur mouvement.
Remarque importante : on parle de plaque chevauchante et de plaque subduite (et non « subductée » qui est un néologisme dérivé de l’anglais). Attention également à
ne jamais confondre « plaque » (ex : plaque pacifique) avec « lithosphère » (qui fait référence à la nature des roches ; ex lithosphère océanique).

II. Morphologie, topographie et dynamisme d’une zone de subduction : Les îles Tonga-Kermadec
 Retourner à un affichage à plus grande échelle (vision globale du planisphère).
NB : planisphère est bien un nom masculin !
 Positionner le curseur sur -20° de latitude et -172° de longitude.
 Zoomer trois fois de suite
 Cliquer sur l’icône « relief 3D ». Une vue en 3D permet de visualiser la zone étudiée. Vous
pouvez modifier l’image à l’aide des touches F1, F2, F3 et du curseur…
5. À partir du bloc diagramme à l’écran, décrivez le relief négatif et positif, Décrivez la localisation
des volcans
 Sortir du relief 3D en appuyant sur la touche « echap ».
 Aller dans le menu « séismes » ; sélectionner « profondeur » puis cliquer sur « superficiel »,
Sélectionner ensuite « dessiner les séismes ». Chaque point jaune représente un séisme
superficiel (inférieur à 60 km).
6. Décrivez leur abondance et leur distribution
 Faire apparaître les séismes de profondeur intermédiaire (entre 60 et 300 km) puis les
séismes profonds (supérieur à 300 jusqu’à 700 km).
7. Concluez sur l’évolution de la profondeur moyenne des foyers sismiques quand on s’écarte de la
fosse.
 Aller dans le menu « outils », sélectionner « coupe » puis « définir ». Deux pastilles bleues
(1 et 2) apparaissent à l’écran. Attraper les pastilles bleues et les déplacer afin que la
pastille 1 soit à -19 de latitude et -179 de longitude et que la pastille 2 soit à -25 de
latitude et -171 de longitude.
 Aller dans le menu « outils », sélectionner « coupe » puis « dessiner ». La coupe apparaît à
l’écran.
8. Que représente ce plan ? Vous indiquerez les plaques lithosphériques (lithosphère océanique ou
continentale) mises en jeu dans cette zone de subduction et leur mouvement.
BILAN 1
9. Indiquez les caractéristiques communes aux deux zones de subduction étudiées ainsi que les
différences.
Problème 2 : Quelle est le moteur de la subduction ?
On cherche à comprendre pourquoi la lithosphère océanique âgée plonge dans l’asthénosphère alors qu’elle flottait avant
sur l’asthénosphère. Cette rupture d’équilibre est due à un changement de masse entre lithosphère et asthénosphère.
Activité : Recherche de l’âge de la rupture d’équilibre de la lithosphère océanique sur l’asthénosphère.
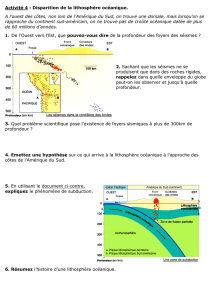
 Principe de la méthode de calcul : L’épaisseur de la lithosphère océanique augmente avec son âge et
sa hauteur H suit une loi qui dit que : H = 9,2  t où t est l’âge en millions d’années. La hauteur
calculée est exprimée en km.

10. Calculez la hauteur H de la lithosphère océanique (précision au 1/ 10) pour les âges suivants : 5,
10, 15, 20, 25, 30, 35 millions d’années. Indiquez les résultats dans la première ligne du tableau (bas de
la feuille).
 Sachant que la lithosphère océanique d’épaisseur H est composée d’une épaisseur h de croûte
océanique (à peu près constante et de l’ordre de 5 km) et d’une épaisseur variable de manteau
supérieur H – h et connaissant les masses volumiques de la croûte (croûte = 2.85) et du manteau
(manteau =3.3) on peut calculer la masse d’une colonne de lithosphère d’une surface de 1 m2 d’après
la formule suivante : ML = croûte x h + manteau x (H – h) (la masse est exprimée en milliers de tonnes).
Croûte océanique
Manteau supérieur
11. Calculez la masse d’une colonne de lithosphère pour les âges 5, 10, 15, 20, 25, 30, 35 millions
d’années. Indiquez les résultats dans la deuxième ligne du tableau.
 On peut de la même façon calculer la masse d’une colonne d’asthénosphère de même épaisseur H
afin de comparer les masses respectives de lithosphère et d’asthénosphère à l’aide de la formule
suivante : MAsth = asthéno x H où asthéno = 3.25
12. Calculez la masse d’une colonne d’asthénosphère pour les âges 5, 10, 15, 20, 25, 30, 35 millions
d’années. Indiquez les résultats dans le troisième ligne du tableau.
Âge en Ma
5
10
15
20
25
30
35
H = 9.2  t
MLithos (103 tonnes)
MAsth (103 tonnes)
13. À quel âge la lithosphère océanique n’est elle plus en équilibre sur l’asthénosphère ? Quelle est
la conséquence de ce déséquilibre ?
14. La lithosphère océanique de la plaque de Nazca qui s’enfonce dans l’asthénosphère au niveau
des Andes est âgée d’environ 40 millions d’années et la lithosphère océanique de la plaque pacifique
qui s’enfonce dans l’asthénosphère au niveau des îles Tonga Kermadec est âgée d’environ 140 millions
d’années. Est-ce en accord avec les calculs effectués précédemment ?
BILAN 2
15. Indiquez quel peut être l’un des moteurs de la subduction.
h = 5 km
H – h
5 Ma
10 Ma
Hauteur H
de
lithosphère
océanique