Université D`AntANANARIVO

1
Université D’AntAnAnArivO
Faculté des Sciences .
Département de Physique
( L.I.E.R )
ALGORITHMIQUE ET PROGRAMMATION
( LANGAGE PASCAL )
APPLICATION A L’ANALYSE NUMERIQUE
Filière : L.I.E.R. - 3èMe Année
Année Universitaire – 2012
RAKOTOSALAMA
EXCLU DE PRÊT
Attention ! Toute reproduction intégrale ou partielle de cet ouvrage , par quelque procédé que ce soit constituerait une contre
– façon sanctionnée par le code pénal

2
CoursAlgoLIER2011B / AlgoLIER2011 / Bureau / Toshiba1
NOTION D’ALGORITHMIQUE
1°) Définitions d’un algorithme , d’un programme et d’une instruction .
 Un algorithme est une suite finie de règles à appliquer dans un ordre déterminé à un nombre fini
de données pour arriver , en un nombre fini d'étapes , à un certain résultat , et cela indépendamment des
données .
Le rôle de l’algorithme est fondamental : il doit être indépendant du langage de programmation dans
lequel il est traduit ainsi que de l’ordinateur qui va exécuter les différentes instructions du programme .
 Un programme est la traduction de l’algorithme pouvant être interprétée puis exécutée par un
ordinateur .
 Une instruction est , soit une action à effectuer , soit une description de données .
Exemple : Afficher a l’écran un message , une expression .
Déclarer une variable
2°) Qualités d’un algorithme ( ou un programme )
Tout programme fourni à l'ordinateur n'est que la traduction dans un langage de programmation d'un
algorithme mis au point pour résoudre un problème donné .
Pour obtenir un bon programme , il faut partir d'un bon algorithme . Il doit posséder les qualités
suivantes:  être clair, facile à comprendre par tous ceux qui le lisent .
 présenter la plus grande généralité possible pour répondre au plus grand nombre de cas
possibles  être d'une utilisation aisée ( facile ) même par ceux qui ne l'ont pas écrit et ce grâce aux
messages apparaissant à l'écran qui indiqueront quelles sont les données à fournir et sous quelle forme elles
doivent être introduites ainsi que les différentes actions attendues de la part de l'utilisateur
 être conçu de manière à limiter le nombre d'opérations à effectuer et la place occupée en
mémoire.
3°) Méthodologie
Trois étapes caractérisent la résolution du problème sur ordinateur :
 préciser les données fournies : les entrées ou input en anglais
 préciser les résultats que l'on désire obtenir : les sorties ou output en anglais .
 déterminer le processus de transformation des données en résultats en utilisant les formules
mathématiques .
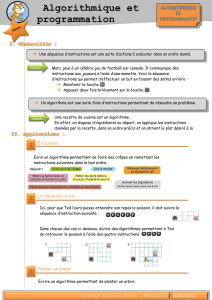
4°) Structures rencontrées en algorithme
Pour représenter n'importe quel algorithme , on dispose les trois possibilités suivantes :
 la structure de séquence qui indique que les opérations doivent être exécutées les unes après les
autres
 la structure de choix qui indique quel ensemble d'instructions doit être exécuté suivant les
circonstances
 la structure de répétition qui indique qu'un ensemble d'instructions doit être exécuté plusieurs fois.
5°) Syntaxe général d’un algorithme ( ou d’un programme )
En général , un algorithme est constitué par :
 Un en – -tête donnant un nom à l’algorithme .
 Une partie déclarative qui regroupe les caractéristiques des variables manipulées dans
l’algorithme .
 Un bloc d’instructions encadré par les mots DEBUT et FIN

3
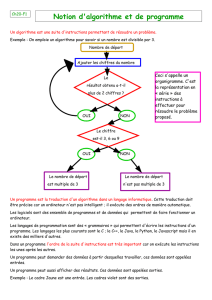
Prenons un exemple :
Exprimer un nombre de secondes sous forme d'heures , minutes , secondes . La seule donnée est le
nombre total de secondes qu’on appelle nsec ; les résultats consistent à trouver 3 nombres entiers h , m , s
L’algorithme doit répondre à la syntaxe suivante :
Algo secondes ( En – -tête )
entier nsec, h, m, s ( Déclaration des variables avec leur type )
Début
écrire "Introduisez le nombre de secondes:"
lire nsec
s  nsec mod 60
m  (nsec \ 60) mod 60 ( Instructions )
h  nsec \ 3600
écrire nsec , "valent : ", h , "heure(s)", m , "minute(s) et", s , "seconde(s)"
Fin.
Remarques :
 \ : quotient entier de 2 nombres entiers ; Ex : 13 \ 2 = 6 , par contre 13 / 2 = 6,5
 mod : reste entier de la division de 2 nombres entiers ; Exemple : – 10 mod 3 = –1
 L’instruction : écrire "Introduire le nombre de secondes:" , donne l’ordre à
l’ordinateur d’afficher à l’écran ou d’imprimer les expressions entre guillemets .
 L’instruction : lire nsec demande au programmeur de taper au clavier la valeur de la
variable nsec .
6°) Définition d’une constante et d’une variable en programmation
 Une constante est une valeur qui ne change jamais tout au long de l’exécution d’un algorithme .
 En programmation , une variable est un objet destiné à recevoir des valeurs (nombres , chaînes de
caractères , ou autres) et à garder la place mémoire nécessaire . Les variables jouent le rôle de "tiroirs" ou ‘’
cases ‘’ dans lesquels on place une valeur durant l'exécution de l'algorithme .
 Alors , l’instruction lire X signifie que l'on introduit dans le tiroir ( ou la case ) baptisé X la valeur
numérique entrée au clavier lors de l'exécution du programme . Le contenu de ce tiroir peut être modifié en y
plaçant le résultat d'un calcul .
7°) Symbole d’affectation ( ou d’assignation ) en algorithme
En algorithme , le symbole d’affectation ( ou d’assignation ) est représenté par une flèche orientée vers la
gauche ( ) . Variable  Expression
Exemple
s  nsec mod 60 signifie que l'on place dans le tiroir s , le résultat de l'opération figurant à droite
de la flèche . Cette instruction se lit : assigner ( ou affecter ) à la variable s la valeur de l'expression de droite
8°) Définition d’une expression en programmation
Une expression est une formule algébrique utilisée pour calculer une valeur . Cette formule fait
intervenir les noms des variables , des constantes numériques et des symboles mathématiques ( " + " :
addition , " – " : soustraction , " * " : multiplication , " / " : division , " \ ": quotient entier de 2 nombres
entiers , " mod ": reste entier de la division de 2 nombres entiers )
On utilise également des fonctions mathématiques usuelles : ln x , sin x , etc., ….
En notation algorithmique , l’opération de concaténation ( juxtaposition de 2 chaînes pour en former
une nouvelle ) est symbolisée par & séparant les 2 chaînes originelles .

4
Exemple :
Notation algorithmique
Traduction en Pascal
A  ‘’ Bon ‘’
B  ‘’ jour ‘’
C  A & B
A : = ‘ Bon ’
B : = ‘ jour’
C : = A + B
C vaut ‘’ Bonjour ‘’
9°) Définition du type d’une variable .
Le type d’une variable est l’ensemble dans lequel la variable prend ses valeurs .
Il y a 2 sortes de types de variables : les types prédéfinis et les types déclarés .
 Les types prédéfinis sont définis dans le langage de programmation ( ici Pascal ) . Il y a 2 sortes de
types prédéfinis : les types scalaires et le type structuré .
Les types scalaires sont : entier , réel , caractère , chaîne et booléen .
Le type structuré est le type tableau .
 Les types déclarés sont créés par le programmeur
Exemples :
Enumération ( Lundi , Mardi , Mercredi , Jeudi , Vendredi , Samedi , Dimanche )
Intervalle Vendredi .. Dimanche
10°) Définition d’un tableau .
Un tableau est une structure de données ayant une dimension et un type déterminés , permettant de
stocker en mémoire plusieurs variables de même type . Ces valeurs sont appelées éléments du tableau ou
variables indicées .
Chacun de ces éléments est repéré par un indice indiquant sa position relative par rapport au début du
tableau .
Dimension : le nombre d’éléments que peut contenir le tableau détermine la dimension du tableau .
Type : désigne la nature des valeurs stockées dans le tableau ( entier ,caractère , chaîne , réel , …. )
Elément : désigne une valeur du tableau .
Indice : c’est un entier naturel dont les valeurs varient de 1 à la dimension du tableau . A chaque valeur
de l’indice correspond une seule valeur dans le tableau .
Exemples :
tableau a(i,j,k),i=0..12 , j=1..5 , k=12..19 d'entier
b(i),i=12..25 de chaînes
c(i,j,k) , i = 1..6 , j = 1..15 , k = 1..9 de réel
Commentaires
Soit la déclaration suivante :
d(i , j) , i = 1..5 , j = 1..3 de réel
Chaque variable indicée doit être décrite dans la partie déclarative de l'algorithme ; la description
comprend trois parties :
1° La première partie décrit le nom de la variable et ses indices : d ( i , j )
2° La deuxième partie décrit pour chaque variable les valeurs que peuvent prendre ces indices :
les entiers i = 1 à 5 et j = 1 à 3 pour la variable indicée d .
3° La troisième partie définit le type de chaque élément constituant le tableau : d ( i , j ) est un
tableau dont les éléments sont des réels .
Remarque : Toutes les composantes d'un tableau doivent être du même type

5
NOTION DE PROGRAMMATION : TURBO PASCAL
1°) Les règles de base de la structure du langage Pascal .
1° Un programme Pascal se compose de trois parties:
un en – tête , caractérisé par le mot PROGRAM
une section déclarative introduite par le mot VAR
une section instruction ou corps du programme , délimitée par les mots BEGIN et END.
Attention : Le programme se termine par un point .
2° L' en – tête sert à donner un nom au programme selon la forme :
PROGRAM identificateur;
3° Un identificateur en Pascal doit débuter par une lettre suivie par un nombre quelconque de lettres ,
chiffres ou de " _ " ( caractère souligné ) . Les identificateurs ne peuvent contenir d'espacement ( caractère
" blanc " ) ou de caractères tels que % , ? , * , . , – ,. mais peuvent être aussi longs que l'on veut ( six pour
la version 3 ) .
4° Les variables doivent faire l'objet d'une déclaration de type de la forme:
VAR
liste des variables : type;
5° Des points-virgules sont obligatoires pour séparer les trois parties et pour séparer les instructions .
6° Les instructions de lecture et d'écriture se traduisent respectivement par READ ( ou READLN ) et
WRITE ( ou WRITELN ) suivis d'une liste de variables ou d'expressions placées entre parenthèses et
séparées par des virgules .
L'ajout du suffixe LN après WRITE ou READ oblige le passage à la ligne suivante lors de l'affichage à
l'écran
7° L'assignation ( ou l’affectation ) se représente par " := "
8° Les opérateurs arithmétiques sont identiques à ceux de la notation algorithmique( ou langage de
description d'algorithme ( LDA ) .
Toutefois , X \ 3600 est traduit par X DIV 3600 . En effet , outre les quatre opérations + , – , * , et / ,
Pascal utilise deux opérateurs supplémentaires :
DIV fournissant la partie entière du quotient de deux nombres entiers
MOD fournissant le reste de la division de deux nombres entiers
Ainsi , 13 / 5 fournit la valeur 2 . 6 ; 13 DIV 5 fournit 2 et 13 MOD 5 fournit 3.
9° Les mots PROGRAM , VAR , BEGIN , END , DIV , MOD , ..... ont un sens précis dans le langage: ce
sont des mots réservés qui ne peuvent être choisis comme identificateurs ( noms ) par le programmeur.
Un certain nombre de mots tels que INTEGER , READLN , WRITE , ... ont une signification prédéfinie .
Pour éviter toute erreur , on évite de les choisir comme identificateur .
10° Les mots du langage et les identificateurs doivent être séparés les uns des autres par un ou plusieurs
‘‘ blancs’’.
2°) Manipulation des nombres.
Pascal reconnaît deux types de nombres : les types entier et réel.
a ) Le type entier.
En algorithme , on placera dans la déclaration des variables , une ligne telle que:
entier age , note qui se traduira en Pascal par :
VAR
age , note : integer;