Document

Page 1 sur 7
Attention au portique… Document : M.Moppert
TS
Physique
Attention au portique…
Exercice résolu
- Enoncé –
Remarques :
- les 4 parties sont indépendantes,
- toutes les réponses seront justifiées.
A. Première partie : Constante de temps d'un circuit RL
On considère un circuit électrique en série comportant :
- un générateur idéal de tension (qui possède une prise de Terre) de force électromotrice E =
10 V,
- une bobine d'inductance L = 1,0 H et de résistance interne r = 10 ,
- un conducteur ohmique de résistance R réglable,
- un interrupteur.
Un dispositif informatisé d'acquisition de données permet de visualiser la tension uR aux bornes du
conducteur ohmique en fonction du temps. A l'aide d'un logiciel de traitement de données, on peut
suivre l’évolution de l’intensité i du courant dans le circuit en fonction du temps. La fermeture de
l’interrupteur, à t = 0 s, déclenche l’acquisition.
1. Faites le schéma du montage. Vous indiquerez :
- l’orientation du circuit,
- la tension E (en convention générateur), ainsi que les tensions uR et uL (aux bornes de la bobine) en
convention récepteur,
- les connexions vers l’entrée du système d’acquisition et vers la masse M.
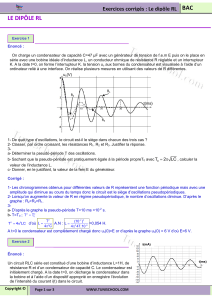
2. Avec R = 90 , on obtient l’enregistrement en annexe.
a) Établissez l'expression de l'intensité I du courant en régime permanent en fonction de E, R et r.
b) Vérifiez que la valeur de l’intensité du courant en régime permanent obtenue sur le graphe de la
figure en annexe est en accord avec l’expression trouvée à la question précédente.
c) Donnez l’expression de la constante de temps du circuit étudié.
d) Déterminez graphiquement la valeur de cette constante de temps et vérifiez que cette valeur est en
accord avec l’expression donnée à la question précédente.
3. On modifie la valeur de la résistance réglable : on a maintenant R = 190 .
a) Calculez la nouvelle valeur I’ de l’intensité du courant en régime permanent.
b) Calculez la nouvelle constante de temps ’ du circuit.
c) Sur l’enregistrement en annexe, représenter soigneusement la courbe de l’évolution de l’intensité i
du courant en fonction du temps.

Page 2 sur 7
Attention au portique… Document : M.Moppert
B. Deuxième partie : Étude d'un circuit oscillant
On réalise ensuite le montage schématisé ci-dessous :
1. Le commutateur est d’abord basculé en position 1 et, ensuite, en position 2 : l'acquisition se
déclenche alors à cet instant. On obtient les courbes ci-dessous (les axes des ordonnées sont gradués
en volts, axe de gauche pour la courbe A et axe de droite pour la courbe B) :
a) Lorsque le commutateur bascule en position 1, le condensateur se charge de façon quasi-instantanée.
Pourquoi ce phénomène est-il très rapide?
b) Attribuez à chaque courbe la tension qui lui correspond.
c) Mesurez la valeur de la pseudo-période des oscillations.
d) Comment peut-on expliquer la diminution d'amplitude des oscillations au cours du temps ?
L, r
R
u1
E
1
K
2
Système
d’acquisition
de données
C
Voie 1
Voie 2
u2
E = 10 V
R = 50 
L= 1,0 H
r = 10 
C = 10 µF
Courbe A
Courbe B

Page 3 sur 7
Attention au portique… Document : M.Moppert
2. On réalise à présent la même expérience en modifiant un seul des paramètres L ou C. Deux cas sont
proposés : dans l’un on a diminué la valeur de L et dans l’autre on a augmenté la valeur de C.
On obtient les enregistrements ci-dessous dessous (les axes des ordonnées sont gradués en volts, axe
de gauche pour la courbe A et axe de droite pour la courbe B) :
Attribuez à chaque cas proposé l’enregistrement (ou ) qui lui correspond.
C. Troisième partie : Oscillations non amorties
Le montage de la deuxième partie est modifié : on enlève la résistance R et on ajoute un dispositif
électronique qui permet de considérer que la résistance globale du circuit est maintenant nulle. Le
commutateur est d’abord placé en position 1 : le condensateur se charge. Le commutateur est ensuite
placé en position 2 : le circuit est le siège d’oscillations électriques non amorties. L’une des armatures
du condensateur porte une charge q dont l'évolution temporelle est de la forme : q(t) = C.E. cos(
0
2
Tp
.t).
1. En déduire l'expression de l'intensité i du courant en fonction du temps dans ce circuit.
2. Quelle est la valeur de l'intensité du courant à t = 0 s, instant où le commutateur vient de passer en
position 2 ?
Courbe B
Courbe A
Courbe B
Courbe A

Page 4 sur 7
Attention au portique… Document : M.Moppert
D. Quatrième partie : Application
La photo ci-contre montre un circuit électrique collé sous la couverture d'un
livre : c'est un oscillateur électrique du type LC, dont la période propre vaut
T0 = 2.
LC
.
Si le livre est tombé « par mégarde » dans le sac d'un client au lieu de passer par la caisse du magasin,
ce circuit va se retrouver, à la sortie, entre les portiques de sécurité. Ces portiques contiennent des
bobines émettant en permanence une onde radio de faible intensité mais de haute fréquence N = 10
MHz, exactement égale à la fréquence propre N0 du petit oscillateur. Dans ces conditions, le circuit
capte l'énergie émise, se met à osciller, et émet à son tour une onde qui vient perturber l'onde des
portiques. La détection de cette perturbation déclenche une alarme.
1. La capacité C du condensateur vaut 5,0 x 10-1 nF. En déduire la valeur de l'inductance L de la bobine
(on prendra 2 = 10).
2. a) Calculez la longueur d'onde de l'onde radio émise par les portiques (on donne la célérité de la
lumière : c = 3,0 x 108 m.s-1).
b) Cette onde radio est-elle mieux diffractée par un obstacle de largeur a = 1 m ou de largeur a =
100m ?
c) Quel est l'intérêt de la diffraction pour ce dispositif ?
ANNEXE

Page 5 sur 7
Attention au portique… Document : M.Moppert
- Corrigé –
A. Première partie : Constante de temps d'un circuit RL
1. Faites le schéma du montage.
a) Établissez l'expression de l'intensité I du courant en régime permanent en fonction de E, R et r.
D'après la loi d'additivité des tensions E = uR + uL et, d'après la loi d'Ohm uR = R.i
La tension aux bornes d'une bobine non idéale a pour expression uL = L.
di
dt
+ r.i
On en déduit : E = R.i + L.
di
dt
+ r.i
Lors du régime permanent, l'intensité du courant est constante : donc
di
dt
= 0 et i = I.
On a alors : E = R.I + r.I et I =
E
Rr+
b) Vérifiez que la valeur de l’intensité du courant en régime permanent obtenue sur le graphe de la figure en annexe est
en accord avec l’expression trouvée à la question précédente.
Graphiquement, on lit : I = 100 mA.
Avec l'expression précédente, on a : I =
109010
= 1,0 x 10-1 A.
La valeur trouvée graphiquement est donc en accord avec l’expression trouvée précédemment.
c) Donnez l’expression de la constante de temps du circuit étudié.
La constante de temps du circuit RL a pour expression :  =
L
Rr+
d) Déterminez graphiquement la valeur de cette constante de temps et vérifiez que cette valeur est en ccord avec
l’expression donnée à la question précédente.
Avec l’expression précédente, on trouve :  =
1090 0,1
= 1,0 x 10–2 s ou 10 ms.
Graphiquement, la constante de temps  est l’abscisse du point d’intersection de l’asymptote à la
courbe et de la tangente à t = 0 à cette même courbe. On trouve : = 10 ms.
La valeur trouvée graphiquement est donc en accord avec l’expression trouvée précédemment.
3. a) Calculez la nouvelle valeur I’ de l’intensité du courant en régime permanent.
I’ =
E
Rr+
soit : I’ =
10190
10
= 5,0 x 10-2 A ou 50 mA.
b) Calculez la nouvelle constante de temps ’ du circuit.
’ =
L
Rr+
soit ’ =
10190 0,1
= 5,0 x 10-3 s ou 5,0 ms.
uL
uR
E
R
L, r
Masse
Entrée