Exercice N°1 : Laser à 4 niveaux

Institut d'Optique, 2° année Examen de Laser 15/12/2011
François BALEMBOIS
1/5
Examen de laser
Durée : 3 heures
Tous documents autorisés
Calculatrice autorisée
Une seule copie
Problème: Pompage par LED d’un laser à colorant
Les performances des diodes électroluminescentes (LED) se sont considérablement
améliorées ces dernières années. Il est maintenant possible d’explorer le potentiel d’un pompage
optique par LED de milieux laser émettant dans le visible. On considère un colorant (molécule
organique) encagé dans une matrice en plastique. Il est pompé à 405 nm et émet à 550 nm. Le
laser est décrit sur la figure 1. Il est pompé transversallement par N=30 LEDs qui ont une surface
émettrice de 1mm par 1mm. Le colorant n’absorbe pas toute la lumière des LEDs au premier
passage : un miroir réfléchissant permet de renvoyer la lumière non absorbée vers le colorant.
Grâce à ce montage, on peut supposer que le milieu est pompé uniformément.
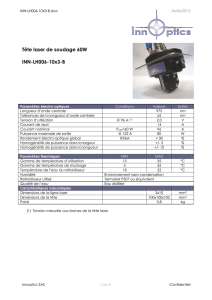
e
e=1mm, d=0,1mm
N LEDs
e
d
Milieu à gain : plastique
dopé par un colorant
Couche protectrice :
plastique non dopé
Miroir
R1=99% Miroir de sortie R2=95 %
Miroir réfléchissant à la
longueur d’onde de
pompe lp
Vue de dessus // au plan des LEDs
Vue de côté au plan des LEDs
T
Figure 1: Montage expérimental du laser à colorant pompé par LEDs.
On utilise les grandeurs et les valeurs suivantes :
d : épaisseur du milieu à gain, d=0,1mm,
e : taille de la surface émettrice de la LED (carré de e par e) : e=1mm,
p : longueur d’onde de pompe, p=405 nm,
 : longueur d’onde laser, =550 nm,
V : volume de colorant pompé par une LED,
n2 : densité de population dans le niveau du haut,
Pabs : puissance absorbée pour une LED, Pabs =5 W,
h : constant de Planck (h=6,62 10-34 Js),
c : vitesse de la lumière dans le vide,
A : coefficient d’Einstein pour l’émission spontanée, 1/A=2 ns,
N : nombre de LEDs utilisées dans le laser, N=30,
R1, réflectivité du premier miroir de la cavité, R1= 99%,
R2, réflectivité du miroir de sortie de la cavité, R2= 95%,
 : section efficace à 550 nm, =10-16 cm2.
Le problème est séparé en trois parties indépendantes. La première partie concerne le
fonctionnement du laser (seuil et de puissance de sortie). La deuxième est centrée sur les
équations de population. La troisième traite de la géométrie de la cavité.

Institut d'Optique, 2° année Examen de Laser 15/12/2011
François BALEMBOIS
2/5
Partie 1 : Oscillation laser
Dans cette partie, le colorant est considéré comme un parfait système à 4 niveaux, pompé en
régime continu. On suppose que les populations ont atteint un état stationnaire.
1.1) En supposant que la densité de population dans le niveau du haut (n2) est connue, donner
l’expression analytique de la puissance d’émission spontanée (en W) émise par le volume V
pompé par une seule LED.
1.2) Lorsque le laser n’oscille pas, on peut considérer que tous les photons de pompe se
convertissent en photons spontanés. Donner l’expression analytique de n2 en fonction des
différents paramètres du laser (en considérant ce qui se passe dans le volume pompé par une
LED).
1.3) Le colorant étant un système à 4 niveaux, le niveau du bas de la transition laser n’est pas
peuplé. Donner l’expression de G0, le gain petit signal pour un passage dans tout le milieu
amplificateur (pompé par les N LEDs).
1.4) Donner la condition sur G0 pour que le laser puisse fonctionner?
1.5) En tenant compte des différentes valeurs, vérifier si le laser peut fonctionner.
1.6) La puissance totale absorbée lorsque le laser est au seuil d’oscillation s’écrit N*Pabsth, où
Pabsth correspond à la puissance absorbée pour une LED au seuil d’oscillation du laser. Donner
l’expression de Pabsth et calculer sa valeur en W.
1.7) En supposant que la cavité n’a pas d’autres pertes que les transmissions des miroirs (notées
T1 and T2), donner l’expression de la puissance de sortie Pout en fonction de Pabs et Pabsth. Donner
la valeur de Pout en W.
1.8) Un colorant est un milieu avec une large bande spectrale d’émission d’environ 50 nm. Décrire
un moyen d’accorder la longueur d’onde d’émission du laser. Faire un schéma du laser pour
illustrer votre réponse.
Partie 2 : Equations de populations
En fait, le colorant n’est pas un système à 4 niveaux parfait. On doit tenir compte de deux niveaux
parasites qui sont décrits sur la figure 2. Les colorants sont des molécules complexes qui ont
beaucoup d’états différents possibles. Suivant le spin des électrons, la molécule de colorant peut
se trouver dans des états dits “singulets” ou dans des états dits “triplets”. L’effet laser est obtenu
avec les niveaux d’énergie des états singulets mais les états triplets peuvent perturber l’émission
laser car la transition 1T-2T est exactement accordée sur la longueur d’onde du laser. Le but de
cette partie est de comprendre l’effet des états triplets sur le laser.
n3
n2
n1
n0
Energie
g
g
A sI
1
2
3
0
spIp n1T
AT sTI
n2T
k2
k1
Etats singulets Etats triplets
2T
1T
Figure 2: Niveaux d’énergie du colorant, nx correspond à la densité de population du niveau considéré.

Institut d'Optique, 2° année Examen de Laser 15/12/2011
François BALEMBOIS
3/5
On utilise les grandeurs et les valeurs suivantes :
AT : coefficient d’Einstein pour l’émission spontanée du niveau 2T au niveau 1T, 1/AT=2 ns,
A : coefficient d’Einstein pour l’émission spontanée du niveau 2 au niveau 1, 1/A=2 ns,
 : section efficace sur la transition 2T-1T à =550 nm, =0,5 10-16 cm2,
 : section efficace sur la transition 2-1 à =550 nm, =10-16 cm2,
p : section efficace pour la pompe (à =405 nm)
k1 : probabilité par seconde pour une molécule de passer du niveau 1T au niveau 1 : k1 = 106s-1
k2 : probabilité par seconde pour une molécule de passer du niveau 2 au niveau 1T: k2 = 107s-1
IP: intensité de pompe en photons/s/cm2
I : intensité laser en photons/s/cm2
 : probabilité par seconde de passer du niveau 3 au niveau 2 et également du niveau 1 au
niveau 0 (ce debit est très important par rapport aux autres débits),
ntot: densité totale de population incluant tous les états possibles.
Comme le débit d’émission spontanée est très important dans le colorant, on peut supposer
que le niveau fondamental n’est pas dépeuplé si bien que n0≈ntot.
2.1) Donner les équations de débit sur les densités de population dnx/dt
Dans les questions allant de 2.2) à 2.4), on suppose un pompage en régime continu et que les
densités de population ont atteint un régime stationnaire.
2.2) Donner les expressions de n2, n1T et n1 en supposant que le laser ne fonctionne pas (I =0).
Utiliser le fait que le débit  est très important par rapport aux autres débits.
2.3) Donner l'expression du gain linéique petit signal g0 (attention, il y a deux transitions laser à
considérer).
2.4) D'après les valeurs numériques des différentes grandeurs, quel est le signe de g0?
Expliquer physiquement ce qui se passe dans le milieu amplificateur.
Dans les questions suivantes (de 2.5) à 2.9)) on suppose un pompage impulsionnel avec une
forme temporelle rectangulaire et une durée tp (quelques centaines de nanosecondes). On
suppose également que le laser ne fonctionne pas (I =0).
2.5) D'après les équations de débit sur les densités de populations, donner la densité de
population dans le niveau du haut en fonction du temps n2(t).
2.6) Donner la valeur du rapport n2 (t=10 ns) sur n2stat, n2stat étant la valeur de la densité de
population du niveau du haut trouvée dans la question 2.2).
2.7) Pour simplifier les calculs concernant n1T(t) et en considérant les différents débits, on peut
supposer que n2(t) varie beaucoup plus rapidement que n1T(t). Ainsi, donner l'expression de n1T(t)
en supposant que n2(t) a atteint sa valeur à l'état stationnaire.
2.8) Donner l'expression du gain linéique petit signal g0(tp) à la fin du créneau de pompage.
2.9) La durée du pompage tp peut varier. Donner la valeur de tp telle que g0(tp)=0.
2.10) Commenter la nécessité de pomper un laser à colorant en régime impulsionnel.

Institut d'Optique, 2° année Examen de Laser 15/12/2011
François BALEMBOIS
4/5
Partie 3 : Conception de la cavité
Comme montré sur la figure 1, le faisceau de cavité doit avoir un rayon complétement différent
dans le plan des LEDs et perpendiculairement au plan des LEDs. Le but de cette partie est de
concevoir une telle cavité en utilisant des miroirs cylindriques concaves. On prend également en
compte la lentille thermique (qui résulte de l'échauffement du milieu à gain à cause du pompage) :
sa distance focale est estimée à f’thermal=500 mm.
Pour simplifier les calculs, on suppose que la lentille thermique est une lentille mince sphérique
située exactement au centre du milieu à gain. A cause des miroirs cylindriques, tout se passe
comme si on avait 2 cavités différentes suivant qu'on regarde dans le plan des LEDs ou
perpendiculairement au plan des LEDs. Les deux cavités sont représentées sur la figure 3. Elles
sont symétriques. On ne prend pas en compte l'indice de réfraction du milieu à gain par simplicité.
Les distances entre les miroirs cylindriques et le centre de la cavité sont fixées à 50 mm. La
longueur d'onde du laser est =550 nm.
50mm
f’thermal= 500 mm
50mm
50mm
f’thermal= 500 mm
50mm
Miroir rayon de courbure Rc
Miroir plan Miroir plan
Vue de dessus // au plan des LEDs
Vue de côté au plan des LEDs
T
Miroir rayon de courbure Rc
Figure 3: Schéma de la cavité dans le plan perpendiculaire au plan des LEDs et dans le plan parallèle au
plan des LEDs.
3.1) On définit Rc1 le rayon de courbure de l'onde propre gaussienne de la cavité juste avant la
lentille thermique et Rc2 le rayon de courbure de l'onde propre gaussienne de la cavité juste
après la lentille thermique. En considérant la symétrie de la cavité, donner la relation Rc1 et Rc2.
3.2) On définit q1 le rayon de courbure complexe de l'onde propre gaussienne juste avant la
lentille thermique et q2 le rayon de courbure complexe de l'onde propre gaussienne juste après
la lentille thermique En utilisant la matrice ABCD de la lentille thermique, donner la relation
entre q1 et q2.
3.3) Déduire de 3.1) et de 3.2) les valeurs de Rc1 and Rc2.
3.4) Comme décrit sur la figure 3, la lentille thermique est la même dans les deux plans
(parallèle ou perpendiculaire au plan des LEDs). Est-ce que les valeurs de Rc1 and Rc2 sont les
mêmes dans les deux plans?
3.5) Dans cette question, on considére le plan parallèle au plan des LEDs
3.5.1) Quel est le front d'onde de l'onde propre gaussienne sur les miroirs?
3.5.2) Quel est la taille du faisceau (rayon) sur les miroirs?
3.6) Dans cette question, on considére le plan perpendiculaire au plan des LEDs
3.6.1) Quel est le front d'onde de l'onde propre gaussienne sur les miroirs?

Institut d'Optique, 2° année Examen de Laser 15/12/2011
François BALEMBOIS
5/5
3.6.2) En considérant les signes des rayons de courbure du front d'onde de l'onde propre
gaussienne, montrer que le plan du waist est nécessairement situé entre le miroir concave et la
lentille thermique.
3.6.3) Le rayon du faisceau laser dans le plan du waist est fixé à w0 = 50 µm dans l'espace
entre le miroir et la lentille thermique. Calculer la position du plan du waist par rapport à la
lentille thermique.
3.6.4) Quelle est la valeur du rayon de courbure Rc des miroirs pour avoir w0 = 50 µm?
3.7) Donner deux schémas montrant l'évolution du faisceau laser dans les plans parallèle et
perpendiculaire au plan des LEDs en tenant compte des valeurs numériques pour les distances
de Rayleigh.