HGT (SCB et SCG) - enseignement Catholique

SCB PHY UAA2 CC 160504
1
Clarifications conceptuelles à l’usage du professeur
Les fluides
Résultante et poussée d’Archimède
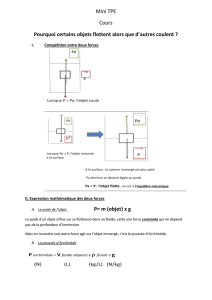
Ces trois schémas représentent un objet O (par exemple un caddie de supermarché sur roulettes…)
subissant deux forces colinéaires, c’est-à-dire de même ligne d’action.
1
La première est exercée par
A et se note :  , ce qui se lit « la force exercée par A sur O ». La deuxième est la force exercée
par B et se note :  .
2
La résultante de deux forces agissant sur un même objet est une force unique qui, à elle seule, a le
même effet que les deux forces réunies. Lorsque les deux forces ont même ligne d'action et même
sens, leur résultante a la même ligne d'action, le même sens et une intensité égale à la somme des
intensités des deux forces (schéma de gauche). Lorsque les deux forces ont même ligne d'action et
des sens contraires, leur résultante a la même ligne d'action, le sens de la plus grande et une intensité
égale à la valeur absolue de la différence des intensités des deux forces (schéma du centre).
Comme la résultante de deux forces est une nouvelle force qui remplace les deux premières, elle ne
s'ajoute pas à celles-ci. Nous avons choisi de représenter les résultantes dans les schémas ci-
dessous à l’aide d’une double flèche, en ayant soin de placer une barre sur les forces qu’elles
remplacent. Remarquons que la recherche d’une résultante n'a de sens que pour des forces agissant
sur un même objet (et n'a donc pas de sens pour des actions réciproques qui agissent toujours sur
des objets différents).
Un objet initialement au repos soumis à plusieurs forces reste au repos (donc en équilibre) si la
résultante de toutes celles-ci est nulle, sinon il se met en mouvement dans la direction et le sens de la
résultante. Dans le cas où toutes les forces s’exerçant sur un objet sont colinéaires (c’est-à-dire ont
une même ligne d’action), il suffit de s’assurer que la somme des intensités des forces s’exerçant
1
Même si l’objet subit encore d’autres forces (la pesanteur, la résistance du sol…), nous ne considérons pour le
moment que les forces horizontales.
2
Les points d’application de ces deux forces sont normalement situés sur la surface de l’objet O, mais par souci
de simplification et de visibilité, nous avons déplacé ces points d’application pour les placer au centre de l’objet O.
Ce déplacement ne pose pas de problème : l’action d’une force sur un objet ne dépend pas de son point
d’application tant qu’il est situé sur la ligne d’action de la force.
HGT (SCB et SCG)
Physique
UAA2
O
O
O
O
O
O

SCB PHY UAA2 CC 160504
2
dans un sens est égale à la somme des intensités des forces s’exerçant dans le sens opposé (voir ci-
dessus schéma de droite, pour un objet sur lequel n’agirait que 2 forces horizontales).
Inversement, si un objet est en équilibre, cela implique que toutes les
forces qu’il subit ont une résultante nulle.
Pour vérifier l’équilibre, il faut s’assurer de n’avoir oublié aucune
force. Par exemple, dans le cas d’une armoire contre laquelle un
homme s’appuie vers la gauche (figure ci-contre), les forces
agissantes sont les suivantes :
 la poussée exercée par l’homme (la force  dirigée vers la
gauche),
3
 le poids de l’armoire (la force 
 dirigée vers le bas),
 la résistance du sol (la force  dirigée vers le haut),
 la force de frottement statique exercée par le sol (la force 
dirigée vers la droite).
Les intensités de ces quatre forces sont telles que tant la résultante des forces horizontales que celle
des forces verticales est nulle, ce que nous résumons en disant que la force totale est nulle.
Le poids d'un objet (ou force de pesanteur subie par l’objet) est la force avec laquelle cet objet est
attiré par la Terre (ou l'astre près duquel il se trouve). Sa ligne d'action est verticale et son sens dirigé
vers le bas. Son intensité se mesure en newtons (N) à l'aide d'un
dynamomètre. Cette intensité dépend de l'endroit où l’objet se
trouve : elle diminue (faiblement) avec l'altitude, augmente
(faiblement) avec la latitude sur Terre, et varie d'un astre à l'autre.
Un objet posé sur un support horizontal est soumis à deux forces :
la force de pesanteur exercée par la Terre sur l’objet vers le bas
(la force 
 dans le schéma ci-contre) et la résistance exercée par
le support sur l’objet vers le haut (la force  ). Ces deux forces
sont égales en intensité car l’objet est en équilibre, mais ne sont
pas des actions réciproques, puisqu’elles agissent sur le même
objet. L’action réciproque à 
 est une force exercée par l’objet sur
la Terre vers le haut (la force  , en pointillés).
4
Cette force n’a
pas d’effet visible sur la Terre tant la masse de celle-ci est
importante. L’action réciproque à  est une force exercée par
l’objet sur le support (la force  , également en pointillés). Elle
peut provoquer la déformation du support selon la nature de celui-
ci.
La masse d'un objet est une mesure de son inertie, c'est-à-dire de sa capacité à résister à l'action
d'une force. En première approche, on peut toutefois considérer qu’elle est liée à la quantité de
matière
5
qui constitue l’objet. Elle se mesure en kilogrammes (kg) à l'aide d'une balance et ne dépend
pas de l'endroit où l'objet se trouve.
En un endroit donné, l'intensité G du poids et la masse m d'un objet sont directement proportionnels :
 , où la constante de proportionnalité (appelée constante de pesanteur et notée g) dépend de
l'endroit où l'on se trouve. Sur Terre, à nos latitudes, au niveau de la mer, g = 9,81 N/kg. La constante
de pesanteur g correspond aussi, par le principe fondamental de la dynamique (F = m.a), à
l'accélération d'un corps en chute libre, et peut donc s'exprimer en m/s².
La masse volumique ρ d'un objet est la masse de cet objet par unité de volume. Elle se calcule en
divisant la masse m par le volume V de l'objet:   
 et s'exprime en kg/m³. Tous les solides
constitués de la même matière ont pratiquement la même masse volumique. Il en est de même pour
3
Dans la suite, nous noterons chaque force par une lettre différente et nous omettrons les indices mentionnant
l’objet-source et l’objet-cible, afin d’alléger les notations.
4
Nous choisissons de représenter les forces secondaires (qui ne s’exercent pas sur l’objet étudié) en pointillés.
Cette représentation permet en outre de bien mettre les actions réciproques en évidence.
5
La quantité de matière (qui se mesure en moles) et la masse (qui se mesure en kilogrammes) ne sont pas
identiques, mais dépendent étroitement l’une de l’autre.

SCB PHY UAA2 CC 160504
3
tous les liquides constitués de la même matière. Cependant, même pour les solides et liquides, cette
valeur peut légèrement varier avec la pression et la température.
Une substance est fluide si elle prend facilement la forme du récipient dans lequel elle se trouve. Elle
est liquide si son volume ne varie (presque) pas sous l'effet d'une pression extérieure, et gazeuse
dans le cas contraire.
Tout objet plongé dans un fluide au repos subit une force appelée poussée
d'Archimède, de ligne d'action verticale, de sens dirigé vers le haut et dont
l'intensité est égale à celle du poids de la quantité de fluide déplacé. Dans un
liquide, l'intensité F de la poussée d'Archimède est donnée par l'expression F =
V.ρ.g, où V est le volume de la partie immergée de l'objet dans le fluide et ρ est la
masse volumique du liquide. Le schéma ci-contre représente un objet assez
lourd (ayant tendance à couler, par exemple un cylindre métallique)
complètement immergé dans de l’eau et suspendu à un dynamomètre par
l’intermédiaire d’un fil. Au repos, l’objet subit trois forces qui s’équilibrent :
 son poids 
, dirigé vers le bas ;
 la poussée d’Archimède 
, dirigée vers le haut ;
 la tension  exercée par le dynamomètre par l’intermédiaire du fil.
Remarquons que conformément au principe des actions réciproques, cette tension  exercée par le
dynamomètre sur l’objet immergé s’accompagne d’une force de même valeur, mais de sens opposé et
exercée par l’objet sur le dynamomètre. On peut donc considérer que le dynamomètre mesure
directement la valeur de la tension. D’ailleurs, en absence de liquide, et donc de poussée
d’Archimède, le dynamomètre mesure directement la valeur du poids de l’objet s’il est maintenu au
repos.
Appliquons à présent la condition d’équilibre énoncée précédemment à la situation de l’objet
immergé : au repos, la somme des intensités des forces s’exerçant vers le haut est égale à la somme
des intensités des forces s’exerçant vers le bas et donc T + F = G. La valeur de la poussée
d’Archimède est donc la différence des valeurs du poids de l’objet et de la tension : F = G – T.
Si on veut immerger un objet assez léger (ayant tendance à flotter, par exemple
un morceau de bois) dans de l’eau, il faut exercer dessus une tension vers le bas,
par exemple par l’intermédiaire d’une poulie posée au fond du récipient, pour qu’il
reste au repos. A ce moment, la condition d’équilibre devient F = G + T : la valeur
de la poussée d’Archimède est la somme des valeurs du poids et de la tension.
Si on laisse cet objet flotter au repos sur l’eau, la poussée d’Archimède 
 qu’il
subit s’oppose alors exactement à son poids 
, et F = G. Notons que le point
d’application du poids se situe au centre de gravité de l’objet, tandis que le point
d’application de la poussée d’Archimède se situe au centre de gravité de la
quantité de fluide déplacé. Dans le cas d’un objet homogène comme le morceau
de bois du schéma, le point d’application de la poussée d’Archimède est situé en-dessous du point
d’application du poids, ce qui peut provoquer des situations de déséquilibre.
Pour déterminer l'expression de la poussée d'Archimède, on peut remplacer
mentalement la partie immergée de l'objet par une portion de fluide de même
forme (et donc de même volume), qui serait évidemment en équilibre : cette
portion de fluide est alors soumise à des forces dont la résultante est nulle. Il y a
donc bien une force appelée poussée d’Archimède qui compense le poids de
cette portion de fluide, il s'agit d'une force de ligne d’action verticale, dirigée vers
le haut, et dont l'intensité est égale à celle du poids du fluide déplacé par l'objet.
Le poids du fluide déplacé s'obtient en multipliant la masse du fluide déplacé et
par la constante de pesanteur g, et cette masse peut elle-même s'exprimer (pour
un liquide) comme le produit de la masse volumique ρ (supposée constante) du
liquide et par le volume du liquide déplacé, c'est-à-dire le volume immergé V de
l'objet. On retrouve ainsi l'expression F = ρ.V.g.
Notons que la poussée d’Archimède est indépendante de la matière dont est constitué l’objet, ainsi
que de sa structure interne (il peut-être creux…). Cela provient du fait que la poussée d'Archimède
qui s'exerce sur un objet plongé dans un fluide au repos est en fait la résultante des forces de
pression exercées par le fluide sur la surface de l'objet, plus importantes sur le bas que sur le haut de
Dynamo-
mètre

SCB PHY UAA2 CC 160504
4
celui-ci. Ces forces de pression
6
ne dépendent que de la profondeur, de la masse volumique du fluide
et de la constante de pesanteur, et non de l’objet sur lequel elles s’exercent.
Les gaz exercent également une poussée d'Archimède sur les objets qui y sont plongés, mais moins
importante que celle exercée par les liquides, car leur masse volumique est moins importante.
En conclusion, un objet lâché au milieu d'un fluide au repos a trois types de comportements
possibles :
 si son poids est supérieur à la poussée d'Archimède (dans le cas où l’objet est homogène,
cela signifie que sa masse volumique est supérieure à la masse volumique du fluide), il coule.
Si l’objet est accroché à un fil qui le maintien en équilibre, il subit trois forces dont la résultante
est nulle : son poids, la force exercée par le fil et la poussée d’Archimède. Si l’objet repose au
fond d’un fluide, il subit trois forces dont la résultante est nulle: son poids, la poussée
d’Archimède et la résistance du fond ;
 si son poids est inférieur à la poussée d’Archimède (dans le cas où l’objet est homogène, cela
signifie que sa masse volumique est inférieure à la masse volumique du fluide), il remonte.
Dans un liquide, il se stabilise à la surface car son volume immergé diminue et la poussée
d'Archimède finit par égaler son poids ;
 si son poids est égal à la poussée d’Archimède (dans le cas où l’objet est homogène, cela
signifie que sa masse volumique est identique à la masse volumique du fluide), il reste
immobile. Si l’objet est accroché à un fil, la force exercée par le fil est nulle.
Lorsqu'un objet se déplace dans un fluide, il subit aussi des forces de frottement et éventuellement
des forces de poussée hydrodynamiques
7
qui s'ajoutent à son poids et à la poussée d'Archimède.
Pression dans les fluides
Lorsqu'un solide pousse un autre solide, la force exercée se répartit sur la surface de contact des
deux solides. Lorsque cette force est perpendiculaire à la surface de contact, elle est appelée force
pressante. Puisqu’une force pressante, contrairement par exemple à la force de pesanteur, ne
s’exerce que sur une partie d’un solide, son effet peut être mis en évidence par les déformations des
objets en contact.
La pression p exercée par le premier objet sur le second est la grandeur physique qui rend compte
de l’effet d’une force pressante sur un objet. Elle se calcule en divisant l’intensité F de la force
pressante par l’aire A de la surface de contact: p = F/A. Elle s'exprime en pascals (1 Pa = 1 N/m²).
Alors que la force pressante est un vecteur, la pression est un nombre (une grandeur scalaire), on ne
peut donc représenter cette dernière par un vecteur.
Un fluide au repos exerce une force perpendiculaire sur les surfaces des objets qui y sont plongés,
mais aussi sur toute surface placée en son sein, quelle que soit son orientation. Il règne donc en tout
point d'un liquide une pression appelée pression hydrostatique. Elle se mesure en pascals (Pa) à
l'aide d'un manomètre.
Dans le cadre du modèle moléculaire, la pression exercée par un fluide sur une surface peut être
expliquée par les chocs aléatoires des molécules du fluide sur cette surface. Ces chocs proviennent
de l’agitation thermique des molécules, qui provient de l’énergie thermique que possède le fluide. Le
modèle des chocs aléatoires permet de comprendre pourquoi la pression ne dépend pas de
l'orientation de la surface.
La pression hydrostatique ne dépend pas de l'orientation de la surface sur laquelle elle s'exerce. Elle
augmente avec la profondeur, et pour une même profondeur elle varie avec la nature du fluide. Dans
le cas d’un liquide non confiné, c’est-à-dire possédant une surface libre, la pression hydrostatique p
en un point est donnée par l'expression p = po + ρ.g.h, où po est la pression à la surface, ρ est la
masse volumique du liquide et h est la profondeur du point.
Pour déterminer l'expression de la pression hydrostatique en un point d'un liquide, on peut isoler
mentalement un cylindre de liquide vertical dont une extrémité se trouve au niveau du point considéré,
et l'autre au niveau de la surface libre du liquide.
Le cylindre est soumis à trois forces verticales:
6
Voir la loi de l’hydrostatique dans la section suivante.
7
Voir la fin de la section suivante.

SCB PHY UAA2 CC 160504
5
 la force 
 due à la pression du liquide sur l'extrémité
inférieure, cette force s'exerce vers le haut ;
 la force  due à la pression atmosphérique sur
l'extrémité supérieure, cette force s’exerce vers le
bas ;
 le poids 
 du cylindre qui s’exerce aussi vers le bas.
Puisque le cylindre est en équilibre, la somme des intensités
des forces s’exerçant vers le haut est égale à la somme des
intensités des forces s’exerçant vers le bas, ce qui peut
s’écrire F = Fo + G.
Les intensités des forces 
 et 
peuvent s'écrire en terme
des pressions p et p0 et de l'aire A de la section du cylindre : F
= p.A et Fo = po.A. Pour sa part, l’intensité du poids peut
s'exprimer en terme de la masse volumique ρ du liquide et de
la profondeur h : G = ρ.A.h.g. En insérant ces expressions dans l’égalité entre les intensités des forces
et en simplifiant, on retrouve bien l'expression p = po + ρ.g.h.
On peut vérifier expérimentalement l’expression de la
pression hydrostatique en considérant la force 
qu’exerce l’eau sur un obturateur
8
refermant l’extrémité
inférieure d’un cylindre creux de section A plongé à une
profondeur h dans un liquide. L’intensité de cette force
peut être mesurée au moyen d’un fil attaché à l’obturateur
et pouvant coulisser librement dans une ou deux poulies
fixées au fond du récipient. La force  à exercer sur
l’extrémité du fil sortant de l’eau pour arriver à décoller
l’obturateur est intégralement transmise par l’intermédiaire
du fil, même si son orientation est modifiée par des
poulies. La valeur de la force  est donc identique à celle
de la force 
 exercée par l’eau sur l’obturateur.
Le principe de Pascal affirme que toute augmentation de pression en un point d'un fluide se transmet
intégralement en tous les points de celui-ci. Si un fluide est confiné (c’est-à-dire entièrement délimité
par des parois solides) dans un tuyau dont les extrémités sont fermées par deux pistons de sections
d'aires A1 et A2, une force  exercée par le premier piston sur le fluide provoque une force  exercée
par le fluide sur le deuxième piston. Les deux forces sont liées par la relation F1/A1 = F2/A2. Si A2 est
plus grande que A1, F2 est donc aussi plus grande que F1. Le principe de Pascal est à la base de
nombreuses machines hydrauliques et peut être abordé en classe en guise d'application.
La mise en évidence de la pression dans les gaz est plus délicate que dans les liquides. Par
exemple, si on tire sur une seringue dont une extrémité est plongée dans l’eau, on constate que l’eau
monte dans la seringue. Pour expliquer ce phénomène, une idée assez naturelle, et qui eut un certain
succès historique dans l’Antiquité et au Moyen Age, est d’affirmer que «la nature a horreur du vide».
En tirant sur la seringue, l’eau s’empresserait de venir combler un espace qui sinon deviendrait vide.
Cette idée est incompatible avec le concept de force. L’eau, initialement au repos, ne peut se mettre
en mouvement par elle-même. Un autre objet a donc dû exercer une force sur celle-ci. Il s’agit en fait
de l’atmosphère qui exerce une force de pression sur la surface libre de l’eau dans le récipient. Cette
force de pression engendre une pression qui se communique en tous points de l’eau selon le principe
de Pascal. En tirant sur la seringue, on provoque la diminution de la pression régnant dans la
seringue par rapport à la pression atmosphérique. C’est donc l’atmosphère qui provoque la remontée
de l’eau dans un endroit où la pression est plus faible.
De manière générale, comme tout fluide, l'air atmosphérique exerce une pression sur les objets qui y
sont plongés. Cette pression est appelée pression atmosphérique et se mesure usuellement en
hectopascals (1 hPa = 100 Pa) à l'aide d'un baromètre. La pression normale au niveau de la mer est
de 1013 hPa. Elle diminue avec l'altitude (comme toute pression dans un fluide) et varie avec les
conditions météorologiques.
9
8
On suppose que l’obturateur (par exemple en plexiglas ou en PVC) a une masse volumique proche de celle de
l’eau, et on ne doit donc pas tenir compte de la poussée d’Archimède qu’il subit.
9
Voir plus loin le paragraphe sur la météorologie.
h
A
h
A