Les mesures de distance en Astronomie

T.P.E. Terminal S. G03 Ecole Alsacienne – Mesure de distance – Année 2003-2004
1
Les mesures de distance en Astronomie :
distances dans le système solaire, distance des galaxies.
Problématique :
Comment mesurer la distance nous séparant d'un corps céleste ?
Plan :
I - La parallaxe, une méthode angulaire
1)La parallaxe diurne
2)La parallaxe annuelle
3) La parallaxe statistique ou séculaire
II - Les céphéides, une méthode photométrique
1) Photométrie, magnitude et loi de Pogson
2) Le diagramme Hertzsprung-Russell et la loi de Tully-Fisher
III- L'effet Doppler & la loi de Hubble, une méthode spectrométrique
1) Les observations
2) L’effet Doppler
3) La loi de Hubble
4) L’âge de l’univers
5) Une remise en question
Introduction générale :
Les mesures de distance en Astronomie mettent en jeu plusieurs
méthodes : une méthode angulaire, photométrique et spectrométrique. La
première utilise la parallaxe (du grec « para » qui signifie « à coté » et
« allaxai » qui signifie «changement »), c’est-à-dire le déplacement par rapport à
l’arrière plan. Nous pouvons ainsi calculer la distance nous séparant de corps
célestes proches. Toutefois la mise en place de distances intrasèques , comme
celles Terre-Lune, permettent d’augmenter le domaine de distances. Ce moyen
laisse vite la place à la méthode photométrique.
Grâce à la découverte des Céphéides, ces étoiles dont la luminosité varie selon la
période, la mesure stellaire a été facilitée. De plus le diagramme Hertzsprung-
Russel a permis d’organiser la luminosité des étoiles selon leur température
émise. A ceci s’ajoute, la loi de Tully-Fisher complétant l’approche de
déduction des distances.

T.P.E. Terminal S. G03 Ecole Alsacienne – Mesure de distance – Année 2003-2004
2
Enfin, la méthode spectrométrique utilise les raies d’absorptions. Or, les raies
observées sont le résultat de l’effet Doppler. Aussi, Hubble en a tiré une loi .
Cette dernière entraine l’étude de la vitesse d’éloignement de l’univers.
I - La parallaxe, une méthode angulaire
Introduction
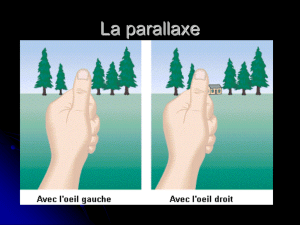
L'expérience est connue : Si, le bras tendu, vous regardez votre pouce
alternativement avec votre œil gauche puis votre œil droit, le pouce semble
sauter d'un point à un autre, On appelle parallaxe ce déplacement par rapport à
l'arrière plan.
On observe un déplacement analogue des planètes ou des étoiles rapprochées
par rapport à l'arrière plan des étoiles éloignées lorsque la position de
l'observateur change, soit parce que la Terre tourne sur elle-même ou parce
qu'elle tourne autour du Soleil. On distingue donc plusieurs types de parallaxe
• La parallaxe diurne: c’est le déplacement apparent journalier d'objets
rapprochés (Lune, planètes) en raison du mouvement de rotation de la Terre.
• La parallaxe annuelle: c’est le mouvement apparent annuel d'étoiles
rapprochées en raison de la révolution de la Terre autour du Soleil.
.• La parallaxe statistique
1) La parallaxe diurne
Pour la mesure de la parallaxe diurne on choisit deux points de la Terre
distants d'un rayon terrestre. L'angle de parallaxe Alpha correspond à l'angle
sous lequel on aperçoit le même objet (astres, planètes ou étoiles proches), par
rapport à un même point (étoile lointaine) infiniment plus éloigné, à partir de
deux endroits sur Terre qui sont éloignés l'un de l'autre d'une distance qui
correspond à un rayon terrestre, soit 6370 km.
Soit x la distance entre la Terre et une planète. La relation suivante donne la
parallaxe en degrés:
r = 2•x•pi•alpha / 360

T.P.E. Terminal S. G03 Ecole Alsacienne – Mesure de distance – Année 2003-2004
3
Comme les parallaxes en astronomie se mesurent sous des angles très petits, on
cherche a obtenir le résultat en secondes d'arc:
r = 2•x•pi•alpha / (360•3600)
On résout par rapport à la distance x (recherchée) et on obtient:
x = r•180•3600 / (pi•alpha)
Calcul de la distance terre-lune, terre-soleil
Pour la Lune, on mesure une parallaxe diurne de 57'2" soit 3422", (donc
depuis la Lune on voit aussi le rayon de la Terre sous un angle de 3422").
on obtient pour la distance Terre-Lune:
a = r•180•3600 / (pi•alpha)
a = 6378•180•3600 / (pi•3422) = 384'000 km.
La parallaxe diurne du Soleil est de 8,79". C'est donc aussi l'angle sous lequel on
verrait le rayon terrestre depuis le Soleil. En introduisant cette valeur dans la
formule (2) on obtient pour la distance Terre-Soleil:
a = 6378•180•3600 / (pi•8,79) = 150'000'000 km.
On appelle cette distance Terre-Soleil "Unité astronomique (UA). C'est une
échelle plus pratique pour les mesures de distances dans le système solaire et
son environnement immédiat.
La parallaxe diurne du Soleil ayant déjà une valeur angulaire très faible, la
parallaxe diurne ne pourra être utilisé pour la mesure de la parallaxe des étoiles,
le rayon terrestre n'offre plus une base suffisante.
2) La parallaxe annuelle
La distance d'un astre peut être donnée par la parallaxe annuelle. Il s'agit
de l'angle sous lequel est vue la distance Terre-Soleil depuis cet astre. Cet angle
est obtenu en mesurant la direction de l'astre à six mois d'intervalle. Durant cette
période, la Terre a parcouru la moitié de son orbite annuelle. Entre la première et
la deuxième observation, elle se trouve de part et d'autre du Soleil et le même
astre est ainsi vue sous 2 angles différents. Cet écart angulaire est, par
construction, le double de la parallaxe. La connaissance de cette parallaxe,
ajoutée à celle de la mesure de la distance Terre-Soleil, donne la distance entre
l'astre et la Terre.
Cette méthode s'applique aux objets du système solaire et aux étoiles proches.
Dans le cas des étoiles, la parallaxe est toujours inférieure à 1" (1° divisé par

T.P.E. Terminal S. G03 Ecole Alsacienne – Mesure de distance – Année 2003-2004
4
3600), donc difficile à mesurer. Au-delà de 1000 années-lumière, les parallaxes
ne sont plus mesurables, il faudra donc utiliser d’autre méthodes.
Pour transformer ces angles, extrêmement petits, en distance, il était nécessaire
de connaître le rayon de l'orbite terrestre, c'est-à-dire la distance moyenne
séparant la Terre du Soleil. On inventa donc une nouvelle unité de distance, le
parsec, (distance à laquelle la parallaxe est égale à 1"). C'est la distance à
laquelle on verrait le demi-grand axe de l'orbite terrestre sous un angle de 1".
Ainsi en utilisant cette formule trigonométrique on peut obtenir la distance de
différents astres ou planètes proches
- La distance D d'une étoile au Soleil, exprimée en l'unité de distance que l'on
veut, est donnée par la relation suivante :
D=R/Pi
Document I-1
- D : distance Soleil-étoile en l'unité choisie
- r : distance Terre-Soleil en l'unité choisie (la même que pour D)
- Pi : parallaxe annuelle exprimée en radian

T.P.E. Terminal S. G03 Ecole Alsacienne – Mesure de distance – Année 2003-2004
5
Exemple de calcul :
En supposant que l'on mesure la parallaxe annuelle d'une étoile à 0.125",
Il faut convertir la parallaxe annuelle en radian.
angle en radian = ( angle en degré / 180 angle en degré = angle en seconde de
degré / 3600)
Donc ( 0.125 / 3600 ) / 180
En admettant que l'on choisit l'année-lumière comme unité, il faut trouve
combien vaut r en années-lumière (al).
r en al = r en km / nombre de kilomètres pour 1 al
r = 150 000 000 km
1 al = 9 500 000 000 000 km
Donc r en al = 150 000 000 / 9 500 000 000 000
Donc :
D = ( 150 000 000 / 9 500 000 000 000 ) / [ ( 0.125 / 3600 ) / 180 ] = 26.05 al
L'étoile se trouve à 26 années-lumière du Soleil.
3) La parallaxe statistique ou séculaire
Elle donne la distance moyenne d’un groupe homogène d’étoiles non liées
physiquement entre elles. La vitesse moyenne de ces étoiles est donc nulle. La
vitesse moyenne mesurée reflète donc le mouvement propre du Soleil.
Appliquée à des étoiles proches dont on connaissait tous les éléments, la
méthode a permis de déterminer le mouvement propre du Soleil. Connaissant le
mouvement propre du Soleil, on peut appliquer la méthode à l’envers à un
groupe d’étoiles et en déduire sa distance.
Cette méthode a été utilisée par Harlow Shapley pour étalonner la loi de
période-luminosité des céphéides. elle est valable de 300 à 1000 AL.
Conclusion
Voilà les trois grandes types de parallaxe qui nous permettent de mesurer
des mesures de distance. Ainsi de nos jours, grâce au satellite d'astrométrie
européen Hipparcos, on connaît maintenant avec une précision de 0.001" les
parallaxes d'environ 100 000 étoiles.