GEOMETRIE

GEOMETRIE
G1. Distinguer : point, droite, segment, alignement de
points.
 LE POINT
Pour représenter un point on dessine une croix.
Pour aider à la description d’une figure, on désigne les points par des lettres.
 LA DROITE
La droite n’a pas de début ni de fin.
 LE SEGMENT
Le segment a des limites, il est limité par deux points.
Ici le segment [AB]
Pour trouver le milieu d'un segment, on peut utiliser la règle graduée et
mesurer.
AB = 6 cm
AM = MB = 3 cm
Le point M est le milieu de [AB].
 ALIGNEMENT DE POINTS
Pour vérifier que les points A, C et D sont alignés, on utilise la règle et l’on
trace une droite. On vérifie qu'elle passe par ces points.
Le point E n’est pas sur cette droite.
Les points E, A et D ne sont pas alignés.

G2 : Angles droits – droites perpendiculaires
Deux droites sont perpendiculaires si elles se coupent en formant un angle
droit.
Pour identifier ou construire des droites perpendiculaires, on utilise une
équerre.
A l'intérieur de cette figure, il y a 4 angles droits.
G3 : Les polygones
Un polygone est une figure plane dont le contour est composé de segments.
Un polygone qui a 3 côtés est un triangle.
Un polygone qui a 4 côtés est un quadrilatère.

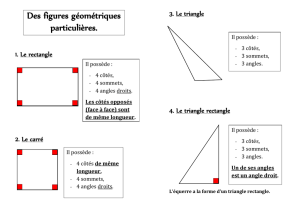
G4 : Carré – Rectangle – Losange – Triangle rectangle
Dans un carré
- il y a 4 angles droits
- les 4 côtés ont la même longueur
Dans un rectangle
- il y a 4 angles droits
- les côtés opposés ont la même longueur (AC = BD et AB = CD)
Le plus grand côté est appelé la longueur.
Le plus petit côté est appelé la largeur.
Dans un losange
 il y a 4 côtés de même longueur
Dans un triangle rectangle
- il y a un angle droit
C’est la moitié d’un rectangle.

2
1
G5 : Le cercle
Pour tracer un cercle j’utilise un compas.
Le centre du cercle est le point O.
Le segment [OB] est le rayon du cercle.
La longueur OB s'appelle aussi le rayon du cercle.
Le segment [AD] est le diamètre du cercle.
La longueur AD s'appelle aussi le diamètre du cercle.
C'est le double du rayon.
G6 Se repérer sur un quadrillage.
A
B
C
D
est
dans la case
B2
est
dans la case
D3
1
2
3
A B C
est sur
le noeud A2
est sur le
noeud C1

G7 : La symétrie par rapport à un axe
Axe de symétrie d'une figure
Quand on plie une figure en deux et que les deux parties se superposent
exactement, le pli est un axe de symétrie.
Une figure peut avoir plusieurs axes de symétrie.
Construire par symétrie sur quadrillage
Attention! Pour utiliser cette technique, il faut que l'axe de symétrie soit une
ligne de quadrillage.
G8 : Construction de figures sur papier uni
Sur du papier uni, pour construire un carré, un rectangle ou un triangle
rectangle, il est nécessaire d'utiliser l'équerre pour construire des angles
droits et la règle graduée (ou le compas) pour tracer des segments de même
longueur.