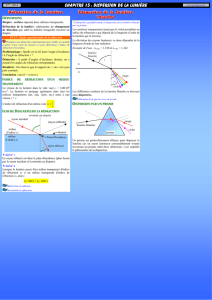
I) Les lois de la réfraction

Montage de physique n°1 :
Expériences portant sur la réfraction de la lumière - Applications
Introduction : Quand on plonge un bâton dans l’eau, on constate qu’il semble se briser à la surface de séparation de l’eau et de
l’air. Cet effet d’optique est dû au phénomène de réfraction qui intervient lorsque la lumière traverse une surface séparant 2
milieux d’indices différents, surface appelée dioptre ; on observe également un phénomène de réflexion partielle .
I) Les lois de la réfraction
1) Mise en évidence et 1ère loi de Descartes :
 Matériel : Une cuve remplie d’eau ; un faisceau laser ; un support avec plusieurs fils plombés.
 Protocole : Dans une cuve remplie d’eau, on dirige le faisceau laser à la surface de l’eau, qui constitue un dioptre air-eau.
 Observations : Au contact du dioptre, le faisceau lumineux incident se sépare en 2 faisceaux :
 Un rayon symétrique au rayon incident par rapport à la normale au dioptre : c’est le rayon réfléchi.
 Un rayon qui se propage dans l’eau avec une direction différente de celle du rayon incident : c’est le rayon réfracté.
 On remarque également que, dans un milieu donné, la lumière se propage en ligne droite. En effet, le milieu considéré
est homogène (même composition en tout points) et isotrope (propagation identique dans toutes les directions).
 Application : A l’aide des fils plombés, on met en évidence la 1ère loi de Descartes : les rayons incident, réfléchi et
réfracté appartiennent au même plan : plan d’incidence.
2) Vérification de la 2ème loi de Descartes :
 Matériel : Un faisceau laser monochromatique, un hémicylindrique en plexiglas posé sur un disque gradué
 Protocole : Un laser émet un pinceau fin et monochromatique sur un demi-disque en plexiglas :
On dirige le rayon incident sur la face plate de l’hémicylindrique. On tourne le demi-cylindre de 10° en 10° et on note les angles
incidents i1 et réfractés i2 que l’on reporte dans le tableau suivant :
i1  0,5°
0
10
20
30
40
50
60
70
80
i2  0,5°
0
sin i1  0,01°
0
sin i2  0,01°
0
sin i1 / sin i2
 0,02°
0
On trace la courbe sin i2 = f(sin i1)
 Observations : On obtient une droite donc le rapport sin i1 / sin i2 est constant pour tout i1.
Ceci vérifie la 2ème loi de Descartes : pour 2 milieux d’indice n1 et n2, l’angle d’incidence i1 et l’angle de réfraction i2 sont
lié par la relation : n1 sin i1 = n2 sin i2
 Application : On peut en déduire l’indice du plexiglas, sachant que nair = 1
La pente de la droite correspond à la valeur recherchée : nplexiglas = 1,5
II) La réfraction selon la nature des milieux
1) Vérification de la loi dans le cas où n1 < n2 :
On dit que le milieu 2 est plus réfringent que le milieu 1.
Remarque : Les indices des différents milieux sont définis par : n=c/v, c étant la célérité de la lumière dans le vide et v étant la
vitesse de propagation de la lumière dans le milieu considéré.
 Protocole : on garde le même dispositif que précédemment.
 Observations et interprétations :
 On observe que pour un angle i1 compris entre 0° et 90°, on peut déterminer un angle i2. Donc à tout rayon incident, lui
correspond un rayon réfracté.
 De plus, i2 < i1 ; ainsi lorsque le rayon de lumière passe dans un milieu plus réfringent, il « se rapproche » de la normale.
 Quand i1 = 90°, c’est à dire pour une incidence rasante, on mesure i2l = 42°. Cette angle est appelé angle de réfraction
limite.
Rq : On peut le vérifier en théorie en utilisant la relation de la 2ème loi de Descartes :
n1 sin i1 = n2 sin i2 i2l = arcsin (n1 / n2) i2l = 41,8°

2) Etude du cas où n1 > n2 :
On dit que le milieu 1 est plus réfringent que le milieu 2.
 Protocole : on tourne le demi-cylindre et on fait pénétrer le faisceau dans le plexiglas par la partie cylindrique :
 Observations et interprétations :
 i2 > i1 ; ainsi, quand la lumière passe dans un milieu moins réfringent, le rayon réfracté « s’éloigne » de la normale.
 Pour i2 = 90°, c’est à dire à émergence rasante, on mesure i1l = 42°.
Rq : En utilisant les lois de Descartes, on trouve : i1l = arcsin (n1 / n2) i2l = 41,8°
 Si i1 > i1l, on observe un phénomène de réflexion totale. Donc, a un rayon incident ne correspond pas toujours un rayon
réfracté.
 Dans le cas n1 < n2, on avait trouvé : i1 = 70° et i2 = 38°.
Dans le cas n1 > n2, on mesure : i1 = 38° et i2 = 70°. Ainsi, on constate que le rayon incident initial devient le rayon réfracté.
Ce résultat montre le principe du retour inverse de la lumière.
3) Bilan :
On peut résumer les différents résultats à l’aide des schémas suivants :
n1 < n2
n1 > n2
n1
n2
i1
i2
i2l
n1
n2
iréfraction
iréflexion
III) Applications
Cf « Montages de physique », Dunod : p. 26 et 27
1) Fibres optiques :
a) A saut d’indice :
 Description : Ce type de fibre est constitué de 2 milieux d’indice différents : le cœur de la fibre (en quartz pur pour
limiter les phénomènes de diffraction sur les impuretés) et la gaine de la fibre.
Le diamètre du cœur de la fibre est de l’ordre de quelques millimètres, voire quelques nanomètres.
 Expérience : Placer le laser à l’une des extrémités de la fibre et montrer qu l’on reçoit la lumière laser à l’autre extrémité.
La fibre optique a permis la propagation de l’onde lumineuse.
 Interprétation : Le rayon se propage dans le cœur de la fibre en subissant de multiples réflexions totales. Ce phénomène
est possible car ncoeur>ngaine et l’angle incident est supérieur à l’angle limite.
 Applications :
 Communication : La fibre optique sert essentiellement à la transmission d’informations. Les différentes sont converties
en signaux lumineux qui se propagent à la vitesse de la lumière (pratiquement) sans
 Médecine : La fibre optique est utilisée pour explorer divers endroits du corps humain (fibroscopie).
b) A gradient d’indice :
 Description : Dans ce type de fibre, le milieu n’est pas homogène : il est dit à gradient d’indice. Le trajet suivi par la
lumière n’est plus rectiligne, il est courbé.
 Expérience : Pour mettre en évidence ce phénomène, on utilise une cuve remplie d’eau et de sel

Rq : il ne faut pas mélanger car le sel permet de constituer un milieu non homogène : la concentration en sel n’est pas la même en
tout point du milieu.
On visualise ensuite le trajet de la lumière laser à travers la cuve.
 Observation : La lumière laser se propageant dans la cuve n’a pas une trajectoire rectiligne : elle se courbe vers le bas.
 Interprétation : Ici le milieu n’est plus homogène : la concentration en sel est supérieure dans le fond de la cuve qu’en
surface. Le gradient de concentration est donc dirigé de haut en bas : c’est la raison pour laquelle le rayon se courbe vers le bas.
 Avantage de ces fibres : Le fait que le rayon se courbe à l’intérieur de la fibre permet de transmettre l’information plus
rapidement.
NB : L’expérience précédente permet également d’illustrer le phénomène de mirage.
2) Réfraction en spectrométrie : mesure d’une longueur d’onde
Un spectromètre à prisme est un instrument d’optique destiné à étudier la composition spectrale d’une source lumineuse.
Un prisme dévie la lumière et on étudie la réfraction des rayons lumineux en fonction de la longueur d’onde.
a) Etude du prisme :
 Schéma du prisme :
 Relations de Descartes pour 2 faces du prisme :
 nair sin(j) = n sin(r) = sin(j)
 nair sin(i’) = n sin(r’) =sin(i’)
 Relations géométriques :
 A = r + r’
 D = i + i’ - A
b) Détermination de la longueur d’onde d’une raie :
 Matériel : Lampe à vapeur de mercure, spectromètre, prisme.
 Mesure de l’angle A du prisme :
Le prisme étant équilatéral, A est l’angle au sommet. On mesure la déviation entre les rayons réfléchis sur les faces du prisme ;
on obtient 2 fois la valeur de A :
On trouve Aexp= 60°
 Mesure d’une longueur d’onde inconnue :
 Etude de 2 raies particulières :
Pour chaque longueur d’onde, il existe un minimum de déviation : valeur de l’angle d’incidence pour laquelle on observe un
minimum de l’angle de déviation. On considère 2 raies de couleurs différentes : par exemple le jaune et le bleu. Connaissant pour
un prisme, la relation qui lie l’indice au minimum de déviation, on en tire donc pour chaque raie une valeur de l’indice.
n = sin[im] / sin(A/2) = sin[(A+D)/2] / (sin(A/2))
 Loi de Cauchy : n = A + B/2
En utilisant les mesures faites précédemment, on en déduit les valeurs de A et B.
 Mesure de la longueur d’onde d’une autre raie : la raie verte.
On se sert de la loi de Cauchy qui nous donne :  = (B / (n-A))1/2

Questions :
 Approximation de l’optique géométrique ? Dans un milieu homogène et isotrope, la lumière se propage en ligne droite suivant
les rayons lumineux.
 Définition de l’indice ? n = c/v
 Loi de Cauchy ? n = A + B/2
 Dioptre ? Surface séparant 2 milieux d’indices différents.
 Chemin optique ? Lab=∫n*dl
 Démonstration de la loi de Snell Descartes ? Principe de Fermat : la lumière pour aller d’un point A à un point B emprunte le
chemin optique stationnaire dLab=0
 Qu’est-ce qui différencie les termes réflexion, réfraction, diffusion ?
Réflexion : Un rayon lumineux qui rencontre une surface est réfléchi.
Réfraction : La lumière qui frappe une surface n’est pas seulement réfléchie, elle pénètre aussi dans le second milieu en
changeant de direction : c’est la réfraction.
Diffusion : Si un faisceau de rayons frappe une surface régulière, chaque rayon est alors réfléchi dans une direction différente.
 Trajet des rayons lumineux à l’intérieur de la fibre optique à gradient d’indice ?
 Fonctionnement d’un réfractomètre ?
 Explication du phénomène de l’arc-en-ciel ?
 Bâton oblique plonge partiellement dans un bac rempli d’eau. Le bâton semble brisé, explication ?
 Expliquer le phénomène de réfraction atmosphérique dans le cas d’observation d’un astre ? Impression de voir l’astre à un
autre endroit de sa position réelle : phénomène de mirage.
 Comment fonctionne un périscope à prisme ?
 Ouverture numérique dans une fibre optique ?
 Explication couche anti-reflet ? Succession de 3 milieux d’indices différents. Le rayon incident subit plusieurs réflexions :
le but est d’éliminer ces réflexions. Couche anti-reflet : condition : même amplitude et conditions d’interférences destructives.