Problème 1. Réalisation d`un filtre.

Régime harmonique 2
Problème 1. Réalisation d’un filtre.
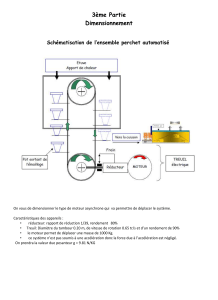
Le circuit représenté ci-dessous est alimenté entre les bornes d'entrée A, B, par un générateur de
tension sinusoïdale de pulsation  réglable, d’impédance interne négligeable qui fournit une tension
u1 de valeur efficace U1constante.
Les inductances sont pures et le condensateur est parfait.
On donne : L = 2.10-3 H; C = 1,0.10-9 F.
1. Exprimer en fonction de , L, C et de
2
Z
, impédance branchée à la sortie, l'impédance
d'entrée
1
Z
, vue des points A1 et B1.
2. Déduire de ce calcul l'impédance caractéristique
c
Z
, définie par la condition
1
Z
=
2
Z
=
c
Z
.
3. Pour quelles valeurs de la pulsation  l’impédance caractéristique est-elle modélisable par
un résistor de résistance Rc ?
Dans toute la suite du problème, on branche à la sortie entre les bornes A2 et B2 un
résistor de résistance Rco égale à la valeur de Rc lorsque la pulsation  tend vers zéro.
Montrer que
Rco =
C
L2
.
4. Donner l’expression de la fonction de transfert
1
2
u
u
)j(H 
, en fonction du seul paramètre
o
x
où
LC2
1
o
. On rappelle que la sortie est fermée sur Rco précédemment
définie.
5. En déduire les expressions du module H et du déphasage retard  de u2 par rapport à u1.
6. Tracer les courbes représentant H(x) en décibels en fonction de log x et (x) en fonction
de log x.
Préciser les asymptotes.
Problème 2. Point matériel en contact avec une demi-sphère.

Un point matériel A, de masse m, est astreint à se déplacer, sans frottement, sur la surface
intérieure d'une demi-sphère creuse S. Cette surface tourne uniformément, à la vitesse angulaire ,
autour de son axe de révolution vertical. Sur la figure, on a représenté le référentiel terrestre noté
Ro= Oxoyozo, supposé galiléen, Ozo étant la verticale ascendante, et le référentiel R= Oxyzo
invariablement lié à S.
On se propose d'étudier le mouvement de A par rapport à R. Pour cela, on projette les relations
vectorielles dans la base de R, et on introduit la quantité étant Ilntensité du champ de
pesanteur terrestre et ro le rayon de la derni-sphère.
1) Exprimer, en fonction des coordonées (x,y,z) de A par rapport à q, de leurs dérivées par
d'entraînement et son accélération de Coriolis qui interviennent d@s la composition des
mouvements de A par rapport à Pet Ao
2) Ecrire vectoriellement la loi fondamentale de la dynamique pour A dans son mouvement
par rapport à 9
En déduire les équations différentielles auxquelles satisfont x, y et z, on mettra la force de
réaction R qu'exerce S sur A sous la forme suivante que l'on justfiera:
r oùr=OA
r
0
3) Quelle est, en fonction de z, l'énergie potentielle de pesanteur de A? On prendra l'origine
de l'énergie potentielle à z = 0.

4) Montrer que la force d'inertie d'entraînement dérive d'une énergie potentielle. Sa
référence étant aussi prise en z = 0.
5) Déduire l'énergie potentielle totale Ep de A.
2 2
w
6) Tracer le graphe de la fonction f u2+ 20 u dans le cas où 0,4.
1
Montrer que Ep
· 0 r.
7) Ci@er qualitativement la tu des différents mouvements en z, suivant la valeur de l'énergie
mécanique totale Em de A dans P( on se placera uniquement dans le cas où
2
0 = 0,4.)
Q2
rapport au temps et de Q : la vitesse d'entrai7nernent de A son accélération

Pour quelle valeur de l'énergie mécanique Em, le point A évolue-t-il en contact avec S dans un
plan horizontal?
Quelle est la cote zm correspondante en fonction de ro?
9) Ecrire l'équation vectorielle traduisant l'équilibre de A par rapport à q Interpréter cette
condition en introduisant le champ de pesanteur g HA, H étant la projection de A
sur l'axe de rotation Ozo.
En déduire la cote ze, à l'équilibre, en fonction de ro. Comparer cette cote à zm et conclure.