1 - Canalblog

- 1 -
582643996 GL 15/04/2017
1
2
2

- 2 -
582643996 GL 15/04/2017
DC
B
A
DC
B
A
DC
B
A
DC
B
A
DC
B
A
DC
B
A
DC
B
A
DC
B
A
DC
B
A
DC
B
A
DC
B
A
DC
B
A
DC
B
A
E=-60
DC
B
A
DC
B
A
DC
B
A

- 3 -
582643996 GL 15/04/2017
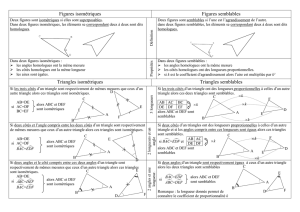
Avec la figure 1 (page 2) comme référence, complète le tableau ci-dessous.
Figures superposables à 1
Figures semblables à 1
Figures déformées par rapport à
1
Définitions :
Figures isométriques : deux figures sont isométriques lorsqu’elles sont parfaitement
superposables. Lorsque deux figures sont isométriques, on appelle isométrie la transformation du
plan qui transforme l’une en l’autre. Cette isométrie peut être une symétrie, une rotation, une
translation ou la composée de plusieurs de ces transformations.
(Voir page 92)
Figures semblables : deux figures sont semblables lorsque l’une est une réduction ou un
agrandissement de l’autre. Lorsque deux figures sont semblables, on appelle similitude la
transformation du plan qui transforme l’une en l’autre. L’échelle de la réduction ou de
l’agrandissement porte le nom de rapport de similitude de ces deux figures.
(Voir page 96)
Lorsque deux figures sont isométriques ou semblables, on appelle :
Côtés homologues, les côtés qui sont images l’un de l’autre
Angles homologues, les angles qui sont images l’un de l’autre
Sommets homologues, les sommets qui sont images l’un de l’autre
(Voir pages 94 et 96)
Propriétés (observation des figures de la page 1 et page 2
Figures isométriques
Figures semblables
Même forme, même grandeur
Même forme, grandeur modifiée
Côtés homologues de même longueur
Côtés homologues de grandeur proportionnelle
Angles homologues de même amplitude
Angles homologues de même amplitude
Remarques
1. Le rapport d’agrandissement de deux figures semblables est plus grand que 1
2. Le rapport de réduction de deux figures semblables est positif et plus petit que 1
3. Si le rapport de similitude est égal à 1, alors la similitude est une isométrie

- 4 -
582643996 GL 15/04/2017
Autres propriétés (périmètre et aire)
Périmètre
Voici le trapèze ABCD. Construis un trapèze EFGH isométrique au trapèze ABCD. Construis ensuite un
trapèze IJKL semblable au trapèze ABCD,(on a commencé le travail en traçant le segment
IJ
Que faut-il
calculer avant de poursuivre la construction ?
Figures isométriques
Comme les symétries, translations, rotations conservent les longueurs, les isométries conservent les
périmètres et les aires des figures.
Figures semblables
Par construction, on a :
Périmètre :
Périmètre de la première figure :
Périmètre de la seconde figure :
Observation :
Conclusion :
Les similitudes multiplient les périmètres par le rapport de la
similitude.
[I J]
DC
B
A
. ..........
. ...........
. ...........
. ............
AB x IJ
BC x JK
CD x KL
DA x LI

- 5 -
582643996 GL 15/04/2017
Aire :
Aire de la première figure : (rappel : aire du trapèze :
( ).
2
B b H
)
Aire de la seconde figure :
Observation :
Conclusion :
Les similitudes multiplient les aires par le carré de leur rapport.
Voir applications sur autre feuille et solutions dans le cahier.
Application intéressante : Les triangles
Si deux triangles ABC et DEF sont semblables, on écrira, en ayant soin de noter les sommets
homologues dans le même ordre.
On en déduira que :
Les angles homologues ont la même amplitude :
C’est-à-dire :
Les côtés homologues sont de longueur proportionnelle
Ce qui peut aussi s’écrire : (k étant le rapport de la similitude)
Cas particuliers : le rapport de similitude est 1 : les triangles sont isométriques :
C
B
A
F
E
D