Bond sur la lune

Comment faire décoller le premier avion ? Problème qu’eurent à résoudre les frères Wright en 1905
(10 points)
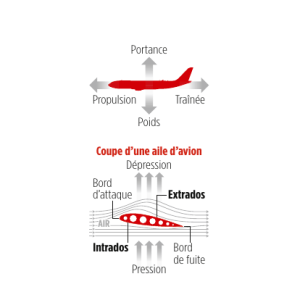
La force qui permet à un avion de se maintenir en l’air est due à l’interaction entre l’air et les ailes.
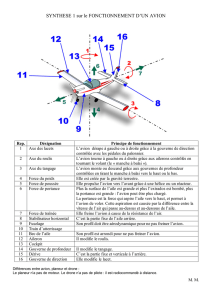
La forme du dessus d’une aile d’avion est convexe (bombée vers l’extérieur).
Si une aile est plate, l’air sur le dessus se déplace à la même vitesse que l’air en dessous.
Quand l’aile est courbée, l’air au dessus accélère (car il a une plus grande distance à parcourir).
L’air plus rapide qui se déplace sur le dessus de l’aile crée une zone de basse pression (air plus dilaté), tandis
que l’air se déplaçant plus lentement sur la face de dessous de l’air crée comparativement une zone de haute
pression.
La différence de pression entraîne une plus forte pression sur le bas de l’aile.
Cette surpression de l’air permet donc à l’avion d’être aspiré :
Cette force exercée vers le haut s’appelle la portance.
Comme elle peut compenser voire supplanter la valeur du
poids, l’avion peut monter.
L’air en frottant sur l’aile crée simultanément une force de
frottement qui freine l’avion : c’est la Trainée.
En vecteur la force résultante exercée par l’air sur les ailes est :
Résultante = Portance + Traînée
Les frères Wright réalisèrent de nombreux essais se lançant du
haut d’une colline avec un planeur (leur futur avion sans ou
avec moteur ne fonctionnant pas), et en déduire que le Flyer I se maintiendrait dans l’air si la vitesse relative
de celui-ci atteignait la valeur de 45 km/h.
Pour obtenir une vitesse de déplacement de l’air qui permet la création de la dépression au dessus de l’aile,
l’avion est équipé d’un moteur qui fait tourner une hélice. L’avion est alors projeté en avant grâce à la force
exercée par l’air sur les hélices. La force ainsi exercée est appelée la Poussée.
Problème pour les frères Wright :
Leur moteur à explosion dont ils disposent est trop limité en puissance sur le Flyer III, la poussée due à
l’action de l’air sur les pales d’hélice en conséquence a une valeur faible de l’ordre de 1000 N.
Les frères Wright déterminèrent que la courte durée des premiers vols provenait du fait que l’avion au
décollage (de masse 400 kg de l’avion avec le pilote) ne pouvait atteindre la vitesse minimale en bout de
piste de 45 km/h en absence de vent, vitesse indispensable pour que la portance supplante le poids.
Remarque : c’est ainsi d’ailleurs que les tous premiers vols s’effectuèrent dans des conditions de vent frontal
important (d’où le choix judicieux du site géographique de leur atelier situé en zone pentue et venteuse).
Leur avion était bien capable de se maintenir en l’air, grâce au moteur, à une vitesse qui permettait la
compensation du poids, mais restait à acquérir une vitesse de 45 km/h en bout de piste au décollage, sans
être tributaire du vent !
Le but de cet exercice est de réaliser différentes études énergétiques qu’ont du réaliser les frères
Wright pour résoudre leur problème d’obtenir une vitesse en bout de piste de 45 km/h.
La valeur de g sera de 10 N/kg dans tout l’exercice.
poids
trainée
portance
poussée
résultante
poids
trainée
portance
poussée
résultante
Sens du
mouvement de
l’avion
Sens du vent relatif
Sens du vent relatif
Sens du
mouvement de
l’avion
Sens du vent relatif
Sens du vent relatif

I ) Décollage de l’avion avec son moteur seul : (4 points)
L’avion de masse 400 kg, se déplace sur un rail de 20 m de long. Sa vitesse initiale est nulle
Approximations :
On considérera la traînée et les forces de frottement de l’avion sur le rail négligeables devant la poussée.
On ne les prendra donc pas en compte dans la résolution de l’exercice.
La poussée due à l’action de l’air sur les pales d’hélice est constante et a une valeur de 1000 N.
On considère de plus que l’avion reste en constant contact avec le rail et qu’il ne décolle pas comme on va le
montrer si la vitesse du vent est inférieure à 10 km/h.
1) Décrire le mouvement de l’avion puis dessiner un diagramme d’interaction pour le système {avion}. (0,5)
2) Représenter qualitativement sur le dessin ci dessous les vecteurs force.
Argumenter à partir des lois de Newton. (1)
3) Représenter un diagramme de transfert d’énergie entre le début et la fin du rail dans le cas où on prend en
compte l’énergie cinétique de l’avion. (0,5)
4) Montrer que la valeur du travail fourni par l’air sur les hélices est de l’ordre de 20 kJ. (0,5)
5) En utilisant le théorème de l’énergie cinétique, déterminer l’expression littérale puis la valeur de la vitesse
acquise par l’avion en bout de rail. (/ 1)
6) En déduire que la vitesse du vent doit être approximativement de 10 km/h pour que l’avion décolle. (0,5)
Résolution du problème de la vitesse au décollage :
Les frères Wright décidèrent alors d’aider l’avion grâce à une catapulte.
Cette catapulte était un derrick de bois, une masse de 650 kg était suspendue en haut du derrick d’une
hauteur approximative de 6,0 m par un ruban relié au nez de l’avion par un système de poulies.
hélice
G
hélice
G
hélice
G
Châssis de l’avion relié par un crochet au câble.
Le pilote actionnait une manette pour le détacher
650 kg
6,0 m
Sens
mvt
Sens
mvt
Pilote allongé
hélice
Châssis de l’avion relié par un crochet au câble.
Le pilote actionnait une manette pour le détacher
650 kg
6,0 m
Sens
mvt
Sens
mvt
Pilote allongé
hélice
Avec moteur seul
20 m de rails
Approximation : frottement fluide avec air et solide avec rails négligés
Avec moteur seul
20 m de rails
Approximation : frottement fluide avec air et solide avec rails négligés

II ) Décollage de l’avion sans moteur avec catapulte : (4 points)
L’avion de masse 400 kg, se déplace sur une distance de 6,0 m de rail correspondant à la distance parcourue
par la masse M. Sa vitesse initiale est nulle
Approximations : On considérera la force de frottement de l’avion sur le rail négligeable devant la force
exercée par la corde. Les frottements au niveau des poulies sont considérés comme nuls.
On ne prendra donc pas en compte aucun frottement dans la résolution de l’exercice.
On considère de plus que l’avion reste en constant contact avec le rail.
Dans cette partie, le moteur ne fonctionne pas.
1) On considère le système {bloc de ciment de masse M en interaction avec la terre}.
Toute l’énergie potentielle de pesanteur n’est pas transformée en énergie cinétique pour le bloc qui
descend : la variation d’énergie est transférée à la corde.
a) Représenter un diagramme de transfert d’énergie rendant compte de cette remarque entre le début et la fin
de la chute du bloc de ciment en prenant en compte l’énergie mécanique du bloc de ciment de masse M en
interaction avec la terre. (0,5)
b) En utilisant le théorème de l’énergie mécanique, déterminer l’expression littérale du travail résistant reçu
par la corde entre le début et la fin de la chute du bloc de ciment en fonction de la masse M du bloc, de la
vitesse finale Vf et de la hauteur h de chute du bloc. (/ 1)
2) On considère le système {avion}.
Tout le travail résistant reçu est transféré par la corde à l’avion sous forme de travail moteur.
a) Représenter un diagramme de transfert d’énergie rendant compte de cette remarque entre le début et la fin
de la chute du bloc de ciment en prenant en compte l’énergie cinétique de l’avion. (0,5)
b) En utilisant le théorème de l’énergie cinétique, déterminer l’expression littérale du travail moteur fourni
par la corde entre le début et la fin de la chute du bloc de ciment en fonction de la masse m de l’avion, et de
la vitesse finale Vf. (0,5)
c) En déduire l’expression littérale de la vitesse Vf acquise par l’avion au bout de 6,0 m en fonction de la
masse M du bloc de ciment, de la masse m de l’avion et de la hauteur h de chute du bloc. (/ 1)
3) Montrer que la valeur du travail fourni par la corde à l’avion est de l’ordre de 15 kJ. (0,5)
III ) Décollage de l’avion avec son moteur et la catapulte : (2 points)
L’avion se déplace sur une distance de 20 m de rail (étant aidé sur 6,0 m par la catapulte).
Approximations : On considérera la traînée et la force de frottement de l’avion sur le rail négligeables
devant la poussée. Les frottements au niveau des poulies sont considérés comme nuls.
On ne prendra donc pas en compte aucun frottement dans la résolution de l’exercice.
La poussée due à l’action de l’air sur les pales d’hélice garde une valeur constante de 1000 N.
1) On considère le système {avion}.On se servira des résultats des questions I ) 4) et II ) 3)
a) Représenter un diagramme de transfert d’énergie rendant compte du rôle l’air sur les hélices et de la
catapulte entre le début et la fin du rail, en prenant en compte l’énergie cinétique de l’avion. (0,5)
b) En déduire l’expression littérale de la vitesse Vf acquise par l’avion au bout du rail. (0,5)
2) En déduire que l’avion peut alors décoller. (1)
M = 650 kg
h = 6,0 m
Sans moteur avec catapulte
6 m de rails
Approximation : frottement fluide avec air et solide avec rails négligés
Les frottements au niveau des poulies sont négligés
La corde est inextensible
F corde /masse
F corde / avion
M = 650 kg
h = 6,0 m
Sans moteur avec catapulte
6 m de rails
Approximation : frottement fluide avec air et solide avec rails négligés
Les frottements au niveau des poulies sont négligés
La corde est inextensible
F corde /masse
F corde / avion