Activité par les élèves : Parallaxe : À quelle distance se

SNC1D&Étude&de&l’Univers&
Activité&par&les&élèves&:&Parallaxe&:&À&quelle&distance&se&trouve&
cette&étoile?&&
Sujets&
distance / unités astronomiques
année-lumière
parsec
parallaxe
Durée&
préparation : 5 min
activité : 25 min
Attentes&particulières&&
SNC1D
A1.8 Évaluer la fiabilité des données empiriques (p. ex., identifier les sources d'erreur et
d'incertitude dans les mesures) ou de l'information recueillie ou la solution à un problème.
A1.9 Analyser et synthétiser les données empiriques ou l'information recueillie (p. ex., traiter les
données, choisir les unités SI appropriées, appliquer des techniques de conversion,
sélectionner des citations, développer les idées principales et secondaires).
A1.10 tirer une conclusion et la justifier.
D1.2 Décrire les principales composantes de notre système solaire et de l'Univers,
qualitativement et quantitativement, en utilisant la notation scientifique et les unités
appropriées.
D2.2 Modéliser une caractéristique des corps célestes (p. ex., comparer la magnitude absolue et
la magnitude apparente à l'aide de sources lumineuses de différentes intensités placées à des
distances variées). [ER]
Introduction&
Puisque les astronomes ne peuvent pas mesurer directement les distances auxquelles se trouvent
les étoiles, ils ont recours à diverses techniques dont la triangulation et la parallaxe, la
comparaison de la magnitude absolue et apparente, et les céphéides ou étoiles variables. La
triangulation est une méthode indirecte de mesure de la distance d’un objet qui consiste à tracer
un triangle imaginaire reliant deux points d’observation et l’objet observé (fig.1). La parallaxe,
qui est utilisée dans cette activité, est la variation apparente de la position d’un objet relativement
proche observé depuis deux points différents. Dans la présente activité, les élèves apprennent
comment utiliser la parallaxe et la triangulation afin de mesurer indirectement la distance des
étoiles. Ils verront également les limites de la parallaxe pour mesurer la distance des objets très
éloignés.

D objet éloigné
distance de l’objet
droites tirées des
points d’observation
X et Y jusqu’à
l’objet en D angles à mesurer
Y
X base de référence Y
Fig.1 Détermination par triangulation de la distance d’un objet
Pour déterminer la distance d’un objet par triangulation, on doit connaître la longueur de la ligne
de base de référence (XY) et les angles entre cette ligne et les deux droites qui relient les points
d’observation X et Y et l’objet en D. Un diagramme à l’échelle fournira ensuite la distance entre
l’objet en D et la base de référence (c.-à-d., la longueur de la droite perpendiculaire à la ligne de
référence. (90°).
Matériel&
1 morceau de papier blanc (5,5 cm × 18 cm)
bureau / table
grande règle
ruban gommé
punaise
marqueur ou crayon
Consigne&de&sécurité&
Aucune
Marche&à&suivre&
1. Expliquez la façon d’utiliser la triangulation et la parallaxe pour déterminer la distance
d’une étoile.
Partie&1&
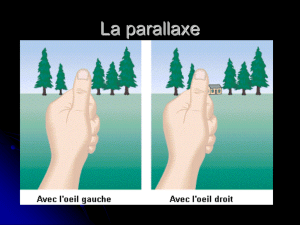
2. Demandez aux élèves de placer un pouce près de leur visage et de fermer un œil. Ils
constateront alors que ce pouce « masque quelque chose » en arrière-plan, par exemple, un
tableau sur le mur. Demandez ensuite aux élèves de changer d’œil mais sans bouger le
pouce. Ils constateront que leur pouce masque quelque chose d’autre en arrière-plan et que
cette chose est très éloignée du premier objet masqué. Demandez-leur de cligner des yeux
en alternance. Il y aura un changement apparent de la position du pouce.
3. Demandez maintenant aux élèves d’allonger le bras et de regarder avec le même œil que la
première fois, le pouce masquant le même objet, puis de changer d’œil. Demandez-leur de

cligner des yeux en alternance. Les élèves constateront que le changement apparent de
position est beaucoup moindre que précédemment.
4. Prédire
Demandez aux élèves de prédire ce qu’il adviendrait s’ils pouvaient allonger le bras
jusqu’à ce que leur pouce entre en contact avec le point sur le mur.
5. Présentez et expliquez la notion du « déplacement angulaire », soit le mouvement apparent
d’un objet relativement proche lorsqu’il est observé depuis deux points d’observation
différents.
Partie&2&
Séparez la classe en groupes de deux ou de trois élèves. Décrivez brièvement le montage en
expliquant que le clou à dessin représente une étoile et qu’ils en observeront le mouvement
apparent depuis deux points de vue légèrement différents.
6. Prédire
Que se produira-t-il au déplacement angulaire du clou à dessin (étoile) lorsque celui-ci sera
placé plus loin?
7. Observer
Collez le bout de papier sur le mur. Placez le bureau à environ 2 m du mur.
8. Collez la grande règle sur le bureau, perpendiculaire au mur et pointant le milieu du bout
de papier. La marque des 100 cm devrait être près du mur.
9. Enfoncez le clou à dessin à la marque des 50 cm de la grande règle.
10. Un élève se place derrière le bureau et aligne son regard avec la grande règle. Il centre son
nez sur la grande règle, les yeux de part et d’autre de celle-ci. Il ferme ensuite l’œil gauche
et demande à un compagnon de faire une marque sur le bout de papier à l’endroit où le
clou à dessin se projette (point A dans la fig.2).
Fig.2 Détermination à la parallaxe de la distance d’un objet
[A. Ligne de visée passant par le clou à dessin, l’œil gauche fermé // morceau de papier // B. Ligne de visée passant par le clou à
dessin, l’œil droit fermé // grande règle]

11. Sans changer la distance d’observation ou hauteur de visée, l’élève ferme l’œil droit et
demande au compagnon de faire une seconde marque sur le morceau de papier à l’endroit
où le clou à dessin se projette (point B dans la fig.2).
12. Les élèves mesurent ensuite la distance entre les points A et B et consignent leurs
observations.
13. On répète les étapes 9 à 12, le clou à dessin placé à la marque des 75 cm puis à celle des
100 cm sur la grande règle. Les points sur le morceau de papier seront identifiés A1, B1,
etc. Il est important que l’élève qui fait les observations place la tête exactement au même
endroit pour toutes les mesures.
14. Expliquer
Demandez aux élèves de décrire et d’expliquer leurs observations, puis de prédire ce qui va
se passer si le clou à dessin (étoile) était placé encore plus loin. Ils devraient examiner le
changement de la distance entre A et B dû à l’accroissement de la distance de l’étoile.
Nettoyage&
Jetez le papier dans le bac de récupération et rangez le reste des accessoires pour utilisation
future.
Qu’estJce&qui&se&produit?&
Partie&1&
Si le pouce touchait à l’objet en arrière-plan (le tableau sur le mur) et qu’il était vu
successivement par un œil et par l’autre, il n’y aurait pas de changement apparent de sa position.
Cela montre que les limites de la parallaxe comme méthode de détermination des distances dans
l’espace, puisque les changements apparents de position des objets très éloignés sont moindres.
Partie&2&
Le déplacement angulaire du clou à dessin (illustré par la distance entre les points A et B sur le
morceau de papier) décroît à mesure que la distance entre le clou et le point de visée augmente.
Les élèves devraient en fin de compte constater que le changement apparent de position est trop
petit pour être mesuré. Par conséquent, les mesures effectuées depuis le sol limitent cette
technique aux étoiles éloignées d’au plus 160 al.
Comment&ça&fonctionne?&
Il y a un déplacement angulaire du clou à dessin parce que l’observateur le voit de deux angles
différents : de son œil gauche et de son œil droit. À mesure que la distance du clou augmente, le
triangle s’étire (sa hauteur croît) et le déplacement apparent de la position du clou (et la
parallaxe, p) est moindre.
Prochaines&étapes&
• Les élèves devraient rechercher les autres techniques (et en examiner les limites)
employées par les astronomes pour déterminer les distances des étoiles.
• Enrichissement : Les élèves pourraient étudier et utiliser la formule !!=!
! (où d est la
distance en parsecs d’une étoile proche et p le parallaxe en secondes d’arc ).
• Extension : Recherchez les parallaxes de diverses étoiles et demandez aux élèves d’en
calculer les distances. Puis pour renforcer davantage les habilités en math, demandez-leur

de transposer leurs résultats en al, en U.A., ou en km, et de les exprimer en notation
scientifique.
Ressources&supplémentaires&
1. ESA – Détermination de la distance d’une étoile au moyen de sa parallaxe :
http://sci.esa.int/science-e/www/object/index.cfm?fobjectid=35616&fbodylongid=1661 (en
anglais seulement)
2. Australia Telescope Outreach and Education – Définitions des termes relatifs à la
triangulation et à la parallaxe :
http://outreach.atnf.csiro.au/education/senior/astrophysics/astrometrytop.html (en anglais
seulement)