Chapitre 4 Figures usuelles et axes de symétrie I

helene.pelle.free.fr
1
Chapitre 4 Figures usuelles et axes de symétrie
I. Figures usuelles
1) Triangles
Définition : un triangle est un polygone ayant 3 côtés.
Vocabulaire :
ABC est un triangle.
A, B et C sont ses 3 sommets.
[AB], [AC] et [BC] sont ses 3 cotés.
A est le sommet opposé au coté [BC].
[AB] est le coté opposé au sommet C.
Feuille 1 vocabulaire
Méthode de reproduction de triangles :
1. on nomme les points
2. place un premier côté
3. on trace avec le compas
Feuille 2 reproduction
2) Quadrilatères
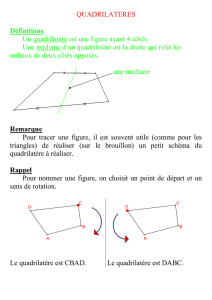
Définition : un quadrilatère est un polygone ayant 4 côtés.
ABCD est un quadrilatère.
A, B, C et D sont ses 4 sommets.
[AB], [BC], [CD] et [DA] sont ses 4 cotés.
A et C sont des sommets opposés.
[AB] et [CD] sont des cotés opposés.
A et B sont des sommets consécutifs.
[AB] et [BC] sont des cotés consécutifs.
[AC] et [BD] sont les diagonales de ce quadrilatère.
A
B
C
A
B
C
D

helene.pelle.free.fr
2
Exemples :
Quadrilatère croisé Quadrilatère concave Quadrilatère convexe
Feuille 3 reconnaître et nommer
Feuille 4 vocabulaire
II. Axes de symétrie
1) Activités – définitions
Activité n°1 constater les axes par reproduction ou pliage
Définition : Une droite (d) est un axe de symétrie d’une figure si les deux parties de la
figure se superposent par pliage le long de cette droite.
Activité n°2 retrouve les erreurs
Activité n°3
Activité n°4
Feuille 5
Feuille 6
2) Triangles particuliers
Activité n°5 ou Atelier : axe de sym d’un triangle.
On remarque que tous les triangles n’ont pas un axe de symétrie. Les triangles qui en
ont un ont deux côtés de même longueur.
On trace un triangle isocèle et son axe de symétrie
Les triangles qui ont un axe de symétrie sont les triangles isocèles.
Un triangle isocèle possède pour axe de symétrie la droite qui passe par le sommet
principal et qui est perpendiculaire à la base.
Certains triangles ont 3 axes de symétrie : les triangles équilatéraux (qui ont 3
côtés de même longueur)

helene.pelle.free.fr
3
Méthode de construction de triangles isocèles
On veut construire ABC un triangle isocèle tel que AB = AC = 4cm ; BC = 6cm.
1. On fait un schéma.
2. On place la base
3. On utilise le compas pour reproduire les deux côtés de même longueur
On construit son axe de symétrie
Vocabulaire
Les deux côtés de même longueur sont [AB] et [AC] donc :
A est le sommet principal
[BC] est la base
On dit que le triangle ABC est isocèle en A
Méthode de construction des triangles équilatéraux
On veut construire IJK un triangle équilatéral de côté 5 cm.
1. On fait un schéma.
2. On trace un côté
3. On utilise le compas pour reproduire les deux autres côtés de même longueur
On construit ses axes de symétrie.
Feuilles 7 et 8
3) Quadrilatères particuliers
Atelier de géométrie 3 : Conjectures
• Le rectangle
Définition :
Un rectangle est un quadrilatère ayant quatre angles droits.
En tracer un, rappeler les conjectures faites en atelier
Propriété:
Il a deux axes de symétries qui passent par les milieux des côtés.

helene.pelle.free.fr
4
Propriété :
Les côtés opposés d’un rectangle sont de même longueur.
Les diagonales d’un rectangles se coupent en leur milieu et sont de même longueur.
• Le rectangle :
On démontre que les côtés opposés ont la même longueur
• On sait que le symétrique de [AB] par rapport à la droite
(d) est ……….
• D’après la propriété : Le symétrique d’un segment par une
symétrie axiale est un
…………………………………………………………………. ..
………………………………………………………
• J’en conclus que AB = ……….
De même on démontre que AD = BC :
• On sait que le symétrique de [AD] par rapport à la droite
(d’) est ……….
• D’après la propriété : Le symétrique d’un segment par une
symétrie axiale est un ………………………………………………………………….
………………………………………………………………..
J’en conclus que ………..= ……….
• Le losange
Définition :
Un losange est un quadrilatère ayant quatre côtés de même longueur.
En tracer un, rappeler les conjectures faites en atelier
Propriété :
Il a deux axes de symétrie : ses diagonales.
Propriété :
Les diagonales du losange se coupent en leur milieu et sont perpendiculaires.
• Le losange:
On démontre que les diagonales sont perpendiculaires et se
coupent en leur milieu :
• On sait que : le symétrique de G par rapport à la droite (FH)
est ………..
• D’après la définition de la symétrie axiale
• J’en conclus que EI = …………. et (EG) est perpendiculaire à
…………….
De même on démontre que I est le milieu de [FH] :
(d)
(d’)

helene.pelle.free.fr
5
• On sait que : le symétrique de F par rapport à la droite (EG) est ………..
• D’après la définition de la symétrie axiale
• J’en conclus que FI = ………….
• Le cerf volant
En construire un
Définition :
Un cerf volant est un quadrilatère ayant deux paires de côtés consécutifs de
même longueur.
Propriétés :
Le cerf volant a un axe de symétrie : une de ses
diagonales.
Les diagonales d’un cerf-volant sont perpendiculaires.
• Le cerf volant
On démontre que les diagonales sont perpendiculaires :
• On sait que : le symétrique de S par rapport à la droite (RT)
est ………..
• D’après la définition de la symétrie axiale
• J’en conclus que SI = …………. et (RT) est perpendiculaire à
…………….
• Le carré
Définition :
Le carré est un quadrilatère ayant quatre angles droits et
quatre côtés de même longueur.
Propriété
Il a quatre axes de symétrie .
D’après la définition du carré, on peut dire que le carré est à la fois un losange et un
rectangle. Il a donc toutes leurs propriétés.
Propriété :