Chapitre 1 : Les angles

Chapitre 1 : Les angles
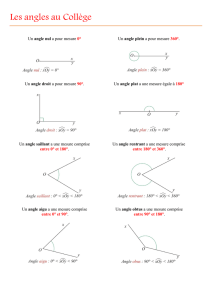
I. Les angles adjacents :
On dit que deux angles sont adjacents si :
 Ils ont le même sommet.
 Ils ont un côté commun.
 Ils sont d’une part et d’autre du côté commun.
Exemple :
 sont deux
angles adjacents.
II. Les angles opposés par le sommet :
On dit que deux angles sont opposés par le sommet si :
 Ils ont le même sommet.
 Leurs côtés sont dans le prolongement l’un de l’autre.
Exemple :
 sont deux angles
opposés par le sommet.

III. Les angles complémentaires et
supplémentaires :
On dit que deux angles sont complémentaire si la somme de
leurs mesures est égale à 90°.
On dit que deux angles sont supplémentaires si la somme de
leurs mesures est égale à 180°.
Exemples :
sont deux angles
complémentaires.
 sont deux angles
supplémentaires.
IV. Les angles correspondants et les angles
alternes internes :
Deux angles déterminés par deux droites coupées par une
sécante sont dits correspondants si :
 Ils sont situés du même côté de la sécante.

 Ils n’ont pas le même sommet.
 L’un est externe tandis que l’autre est interne.
Deux angles déterminés par deux droites coupées par une
sécante sont dits alternes-internes si :
 Ils sont situés d’une part et d’autre de la sécante.
 Ils n’ont pas le même sommet.
 Ils sont tous les deux internes.
Exemples :
 sont deux
angles correspondants.
 sont deux
angles alternes internes.
Propriétés :
1. Si deux droites coupées par une sécante sont parallèles
alors les angles correspondants ou les angles alternes
internes déterminés par ces droites sont égaux.
2. Si deux angles correspondants ou deux alternes-
internes déterminés par deux droites coupées par une

sécante sont égaux alors ces deux droites sont
parallèles.
V. Les angles inscrits :
Dans un cercle, un angle inscrit est un angle dont le sommet
est sur le cercle et dont les côtés coupent le cercle.
Dans un cercle, un angle au centre est un angle dont le
sommet est le centre du cercle et dont les côtés coupent le
cercle.
Exemples :
est un angle inscrit.
 est un angle au centre.

Remarques :
On dit que l’angle 
intercepte l’arc FD que l’angle 
intercepte l’arc BC.
Théorème de l’angle inscrit :
Dans un cercle, deux angles inscrits
interceptant le même arc sont égaux.
Théorème de l’angle au centre :
Dans un cercle, si un angle inscrit et un
angle au centre interceptent le même arc,
alors la mesure de l’angle au centre est le
double de celle de l’angle inscrit.