détermination de la masse de Jupiter

Terminale S www.sciencesphysiques.info
TP de Sciences Physiques n°11 : détermination de la masse de Jupiter Page 1 / 4
TP de Sciences Physiques nÀ11
Détermination de la masse de Jupiter
Objectifs de la séance
Répondre enfin à la question : « comment fait-on pour peser une planète ? »
Découvrir les lois de Kepler et appliquer la troisième loi pour déterminer la masse d’un astre.
Utiliser un logiciel de simulation (stellarium) pour prendre des mesures astronomiques.
Utiliser un tableur pour valider une loi théorique.
Compétences mise en œuvre
Les compétences mises en jeu sont essentiellement « réaliser », « analyser » et « valider ».
Réaliser : prendre des mesures précises grâce au logiciel stellarium.
Analyser : utiliser les valeurs mesurées dans un tableur pour vérifier une loi.
Valider : confronter les résultats obtenus avec les valeurs de référence et conclure.
Introduction
Johannes Kepler est un astronome allemand, contemporain de Galilée, célèbre pour avoir étudié l’hypothèse
héliocentrique de Nicolas Copernic, et surtout pour avoir découvert que les planètes ne tournent pas en cercle
parfait autour du Soleil mais en suivant des ellipses. Il élabora trois lois qui décrivent très précisément les
mouvements des astres, connues sous le nom de « lois de Kepler ».
Enoncé des trois lois de Kepler :
Les planètes décrivent des trajectoires elliptiques dont le Soleil est un foyer.
Le mouvement de chaque planète est tel que le segment de droite reliant le Soleil et la planète balaie des
aires égales pendant des durées égales (loi des aires).
Ces deux lois furent publiées dans « Astronomia Nova » en 1609, où Johannes Kepler fut également le
premier à émettre l’hypothèse d’une rotation du Soleil sur son axe. En 1618 viendra sa troisième grande loi :
Pour toutes les planètes, le rapport entre le cube du demi grand axe de la trajectoire et le carré de la
période est le même. Cette constante est indépendante de la masse de la planète.
Mathématiquement, la troisième loi de Kepler s’exprime sous la forme : k
a
T
3
2
=
où T est la période de révolution de la planète
a est le demi grand axe de la trajectoire elliptique de la planète
k est une constante (et ne dépend pas de la planète considérée)
Ces trois lois, découvertes à partir de la seule observation astronomique, ont été démontrées plus tard à partir
de la deuxième loi de Newton. Cette démonstration permet d’exprimer la constante k, qui dépend de
constantes universelles (π et G) et de la masse M de l’astre autour duquel tourne l’astre considéré :
GM
4
a
T
2
3
2
π
=
Nous allons, dans ce TP, étudier les mouvements des quatre satellites galiléens de Jupiter et vérifier
expérimentalement la troisième loi de Kepler. En outre, nous allons, grâce à cette loi, déterminer la masse de
l’astre autour duquel tournent ces satellites, à savoir la planète Jupiter.
Les quatre grands satellites de Jupiter ont été découverts par Galilée en janvier 1610 (voir document page 4).

Terminale S www.sciencesphysiques.info
TP de Sciences Physiques n°11 : détermination de la masse de Jupiter Page 2 / 4
II - Mesures astronomiques
Dans le logiciel « stellarium », effectuer le travail suivant :
rechercher (F3) Jupiter et le fixer au centre de l’écran (barre d’espacement).
supprimer le sol et l’atmosphère afin de pouvoir observer Jupiter en continu (24h/24h).
choisir une monture équatoriale afin d’observer les trajectoires des satellites dans un plan fixe.
régler le grossissement (molette de la souris) afin d’observer ses quatre grandes lunes.
arrêter le défilement automatique du temps puis, manuellement, faire avancer le temps de quelques
heures ou jours et observer la rotation des satellites autour de Jupiter. Le grossissement doit être choisi le
plus grand possible tout en s’assurant que Callisto reste continuellement visible durant sa révolution. Une
fois ce paramétrage effectué, noter la valeur précise du champ de vision, noté FOV et exprimé en degré
(Field of vision, de l’ordre de 0,200° en général), et ne plus toucher au grossissement jusqu’à la fin des
mesures. Noter aussi la distance Terre – Jupiter, notée D
TJ
donnée par le logiciel.
consigner dans le tableau suivant, pour chaque satellite, une date t
1
de début d’occultation par Jupiter et
la date t
2
après une révolution (occultation suivante). On prendra comme précision des mesures la
minute.
quand le satellite passe au plus loin de Jupiter, mesurer sur l’écran (au double décimètre) la distance entre
le centre de Jupiter et celui du satellite. Reporter cette distance, qui correspond au rayon (noté R
écran
) de
la trajectoire du satellite, dans le tableau.
Satellite Date t
1
d’occultation Date t
2
après un tour Rayon de l’orbite (R
écran
en cm)
Io
Europe
Ganymède
Callisto
dans le menu « fenêtre de configuration » (F2), sous l’onglet « outils », sélectionner « positionnement du
disque » afin de faire apparaître l’oculaire du télescope virtuel puis mesurer son diamètre, qui correspond
à la hauteur de l’écran (D
télescope
= H
écran
en cm).
Remarque : la loi de Kepler fait intervenir le demi-grand axe d’une trajectoire elliptique. Pour simplifier
notre étude, nous considèrerons les trajectoires des satellites de Jupiter comme circulaires et non elliptiques.
Le demi-grand axe « a » de l’ellipse correspond alors au rayon « R » du cercle. Cette approximation est
cohérente car les trajectoires des satellites galiléens sont légèrement elliptiques.
II - Analyse des résultats et conclusion
1. Analyse théorique
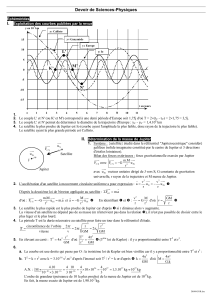
Le champ de vision (FOV) noté θ et exprimé en degrés, est l’angle correspondant à la largeur du disque
oculaire du télescope (c’est-à-dire ici à la hauteur de l’écran). L’angle α correspond en revanche au rayon de
la trajectoire du satellite considéré.
écran
écran
H
R
=
θ
α
θ
H
écran
R
écran
α

Terminale S www.sciencesphysiques.info
TP de Sciences Physiques n°11 : détermination de la masse de Jupiter Page 3 / 4
Par ailleurs, l’angle α est l’angle sous lequel on voit l’objet depuis la Terre :
Exprime la tangente de l’angle α dans le triangle rectangle TJS.
En t’appuyant sur l’approximation des petits angles (α est ici très petit puisque D
TJ
est très grande devant
R
sat
), exprime le rayon réel de l’orbite du satellite R
sat
en fonction de l’angle θ (FOV), de la distance
réelle Terre – Jupiter D
TJ
, et des distances mesurées sur l’écran R
écran
et H
écran
.
Dans un tableur, rentre le tableau de données suivant :
FOV (°) à chercher sur stellarium
FOV (rad) à calculer
D
TJ
(UA) à chercher sur stellarium (1 UA = distance Terre Soleil = 150 millions de km)
D
TJ
(m) à calculer
H
écran
(cm) à mesurer sur l’écran
Réalise puis exploite ensuite le tableau suivant :
Satellite Période (s) R
écran
(cm) Angle α (°) R
sat
(m) T
2
(s
2
) R
3
(m
3
)
Io
Europe
Ganymède
Callisto
Après avoir rempli le tableau de calcul, trace le graphique T
2
= f(R
3
).
Confronte, en justifiant, le résultat obtenu à un modèle théorique et valide le modèle de Kepler grâce au
coefficient de détermination.
Calcule la masse de Jupiter d’après l’expression de la troisième loi de Kepler.
Cherche la masse de Jupiter théorique et discute de la précision du travail effectué. Evalue en justifiant si
l’imprécision provient plutôt des mesures de distances ou des mesures de périodes.
D
TJ
R
sat
Jupiter
Satellite
Observateur
terrestre
α

Terminale S www.sciencesphysiques.info
TP de Sciences Physiques n°11 : détermination de la masse de Jupiter Page 4 / 4
Notes manuscrites de Galilée – 7 au 15 janvier 1610 (Padoue, Italie)