1 Modélisation d`un télescope de Newton 2 Étude d

EXERCICES SUR LE TÉLESCOPE 1
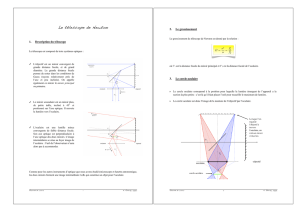
1 Modélisation d’un télescope de Newton
On réalise un télescope de Newton à l’aide d’un miroir sphérique de 10 cm de distance focale et 4,0 cm de
diamètre, d’un miroir plan et d’une lentille convergente de 2,0 cm de distance focale.
Le centre du miroir secondaire est situé sur l’axe optique du télescope à 2,0 cm du foyer du miroir principal.
On observe à l’aide de ce télescope, un objet AB situé à l’infini. A étant sur l’axe du télescope. Le miroir
principal donne de cet objet AB une image A1B1de 8,0 mm de hauteur.
1. Faire un schéma à l’échelle 1/1 sur lequel seront représentés les deux miroirs, la lentille oculaire et l’image
AB.
2. Tracer un des rayons qui permettent de construire l’image A1B1et en déduire l’angle θsous lequel est
vu l’objet AB depuis le lieu d’observation.
3 Construire l’image A2B2donnée par le miroir plan ainsi que l’image définitive A’B’.
4. Calculer l’angle θ0sous lequel est vu l’image A’B’ et en déduire le grossissement du télescope.
5. Vérifier que ce grossissement est bien égal au rapport de la distance focale de l’objectif sur celle de
l’oculaire.
6. Tracer la marche d’un rayon quelconque issu de B.
7. Quelle est la distance minimale qui doit séparer le centre du miroir secondaire du foyer du miroir
principal ? de quoi dépend-elle ?
2 Étude d’une notice de télescope
!"#$%&%$'()*+,*$'+,(#-.,
!"#$%&'()&"*+#,-*+)$%.'/"0.+#.+1.2)"*3
!"#$%&'()*#+"#,%'*)-./*#0*#1*2,."#3#'4&(0*#04+"#5($.($#)/6%$(7+*#0*#89#-5#0*#0(),&"-*#:.-&'*#*,#;<9#-5#0*#
0(&5=,$*<#04+"#5($.($#/'&"#*,#04+"*#'*",(''*#-.">*$?*",*#0*#@<9#-5#0*#0(),&"-*#:.-&'*A
B*#-*",$*#0+#5($.($#)*-."0&($*#*),#)(,+%#)+$#'4&C*#./,(7+*#0+#,%'*)-./*#3#@<9#-5#0+#:.D*$#0+#5($.($#/$("-(/&'A#
!"#.E)*$>*#3#'4&(0*#0*#-*#,%'*)-./*<#+"#.EF*,#GH#)(,+%#3#'4(":("(A#G#%,&",#)+$#'4&C*#0+#,%'*)-./*A#B*#5($.($#
/$("-(/&'#0.""*#0*#-*,#.EF*,#GH#+"*#(5&?*#G8H8#0*#I<9#55#0*#6&+,*+$A
8A J&($*#+"#)-6%5&#3#'4%-6*''*#8K8#)+$#'*7+*'#)*$.",#$*/$%)*",%)#'*)#0*+C#5($.($)<#'&#'*",(''*#.-+'&($*#*,#'4(5&?*#
G8H8A
@A L$&-*$#+"#0*)#$&D.")#7+(#/*$5*,,*",#0*#-."),$+($*#'4(5&?*#G8H8#*,#*"#0%0+($*#'4&"?'*#!#).+)#'*7+*'#*),#>+#
'4.EF*,#GH#0*/+()#'*#'(*+#04.E)*$>&,(."A
MA N."),$+($*#'4(5&?*#G@H@#0.""%*#/&$#'*#5($.($#/'&"#&(")(#7+*#'4(5&?*#0%:("(,(>*#G4H4A
;A N&'-+'*$#'4&"?'*#!4#).+)#'*7+*'#*),#>+#'4(5&?*#G4H4#*,#*"#0%0+($*#'*#?$.))())*5*",#0+#,%'*)-./*A
OA P%$(:(*$#7+*#-*#?$.))())*5*",#*),#E(*"#%?&'#&+#$&//.$,#0*#'&#0(),&"-*#:.-&'*#0*#'4.EF*-,(:#)+$#-*''*#0*#
'4.-+'&($*A
QA L$&-*$#'&#5&$-6*#04+"#$&D."#7+*'-."7+*#())+#0*#HA
RA S+*''*#*),# '& #0(),&"-*# 5("(5&'* #7+(#0.(, # )%/&$*$#'*#-*",$*# 0+ #5($.($# )*-."0&($*# 0+#:.D*$# 0+#5($.($#
/$("-(/&'#T#U*#7+.(#0%/*"0V*''*#T
4)-#.+#,-*.+*")&/.+#.+)$%.'/"0.3
!"#$"!%&'()*+'",-./012)3'45
66786999"%:;12*4<1&5
L%'*)-./*#-&,&0(./,$(7+*#-.5/&-,#5.,.$()%A
W'#*),#/&$,(-+'(=$*5*",#(",%$*))&",#/.+$#'*)#.E)*$>&,(.")#/'&"%,&($*)A
X($.($)#&'+5("%)#?&$&",()A
N&$&-,%$(),(7+*)#Y#
#0(&5=,$*#+,('*#Y#88;#55#Z
#'."?+*+$#:.-&'*#J#Y#8#999#55#Z
#.+>*$,+$*#$*'&,(>*#JKU#Y#[#Z
#/.+>.($#)%/&$&,*+$#Y#8<844#Z
#5&?"(,+0*#),*''&($*#'(5(,*#&--*))(E'*#Y#8@<;#Z
#-'&$,%#Y#MQ8"#Z
#?$.))())*5*",)#Y#O9"#Z#I9"#Z#899"#Z#8Q9"#Z#@O9"#Z
#.-+'&($*)#-.+'&",#M8<RO#55#Y#@9#55#Z#8@<O#55#Z#;#55#Z
#H&$'.2#-.+'&",#M8<RO#55#Y#@"#Z
#?$.))())*5*",#5&C(5+5#/$&,(7+*#Y#@IO"#Z
#5.",+$*#%7+&,.$(&'#Z
#-6*$-6*+$#Y#O"#$#Z
#,$%/(*0#Y#&'+5("(+5#$%?'&E'*#*"#6&+,*+$#Z
#/.(0)#Y#8@#\?A
!"#$%&'($)*
=>6?#]*-6*$-6*^#'*#)*")#0*)#5.,)#).+'(?"%)A
=>#?#P%$(:(*^#'*#-&'-+'#0*#'4.+>*$,+$*#$*'&,(>*A
=>@?#_,('()*^#'*#/.+>.($#)%/&$&,*+$#/.+$#-&'-+'*$#'*#/'+)#:("#0%,&('#>()(E'*#)+$#'&#B+"*#`0LVB#5.D*"#a#MI;#;99#\5bA
=>7?#]*,$.+>*^#'&#>&'*+$#0*#'&#-'&$,%#*"#-.5/&$&",#'&#)+$:&-*#7+(#-.''*-,*#'&#'+5(=$*#0&")#'*#,%'*)-./*#*,#-*''*#
0*#'&#/+/(''*#0*#'4c('#`0(&5=,$*#0*#Q#55<#'&#"+(,bA
=>A?#P%$(:(*^#'*)#>&'*+$)#0*)#?$.))())*5*",)#("0(7+%)A
!"#"#!"de9Re]@A.0, #f&?*#8KM
T 28 Télescope Sky-Watcher 114/1000 équatorial.
Télescope catadioptrique compact motorisé.
Il est particulièrement intéressant pour les observations planétaires.
Miroirs aluminisés garantis.
Caractéristiques :
Pdiamètre utile : 114 mm ;
Plongueur focale F : 1000 mm ;
Pouverture relative F/D : 9 ;
Ppouvoir séparateur : 0◦001,100 ;
Pmagnitude stellaire limite accessible : 12,4 ;
Pclarté : 361×;
Pgrossissements : 50×; 80×; 100×; 160×; 250×;
Poculaires coulant 31,75 mm : 20 mm ; 12,5 mm ; 4 mm ;
PBarlow coulant 31,75 mm : 2×;
Pgrossissement maximum pratique : 285×;
Pmonture équatorial ;
Pchercheur : 5×24 ;
Ptrépied : aluminium réglable en hauteur ;
Ppoids : 12 kg.
QUESTIONS
1. Rechercher le sens des mots soulignés.
2. Vérifier le calcul de l’ouverture relative.
3. Utiliser le pouvoir séparateur pour calculer le plus fin détail visible sur la Lune (dTL moyen =384 400 km).
4. Retrouver la valeur de la clarté en comparant la surface qui collecte la lumière dans le télescope et celle
de la pupille de l’œil (diamètre de 6mm la nuit).
5. Vérifier les valeurs des grossissements indiqués.
1

EXERCICES SUR LE TÉLESCOPE 2
CORRECTION : Modélisation d’un télescope de Newton
1. Schéma : voir figure 1. L’objet est à l’infini, l’image A1B1est au foyer image F’1.
2. L’angle sous lequel est vu l’objet AB est égal à l’angle sous lequel on voit A1B1du miroir.
Donc θ=A1B1/f0
1soit 0,80/10 d’où θ=8,0×10−2rad.
3. L’image A2B2donnée par le miroir plan est symétrique de A1B1par rapport au plan du miroir. Elle se
forme dans le plan focal objet de l’oculaire (télescope afocal). L’image définitive est rejetée à l’infini.
4. L’angle θ0sous lequel est vue l’image définitive est égal à l’angle sous lequel est vu A2B2depuis le centre
optique de la lentille de l’oculaire. Donc θ0=A1B1/f0
2soit 0,80/2,0 =0,40 rad.
Le grossissement est donc égal à G=θ0/θ. Soit G=5,0.
5. Calcul du rapport des distances focales : G=f0
2/f0
1=10/2,0 =5,0. Les grossissements sont identiques.
6. Tous les rayons issus du point B ont la même direction, ils convergent au point B2et donc ressortent tous
parallèles.
7. Pour que l’oculaire ne soit pas un obstacle supplémentaire dans le tube pour la lumière, il faut que le
centre de la lentille de l’oculaire soit à une distance supérieure à celle du rayon du tube (moitié du diamètre
utile).
CORRECTION : Étude d’une notice de télescope
1.iSens des mots.
Diamètre utile : diamètre de l’ouverture du tube.
Longueur focale : distance focale du miroir principal.
Magnitude stellaire : mesure de l’éclat des corps célestes. Une étoile de magnitude 4 est plus lumineuse
qu’une étoile de magnitude 5 ; la magnitude des objets les plus brillants est représentée par des nombres
négatifs. Deux étoiles dont le rapport des intensités lumineuses est de 100 différent de 5 magnitudes. Deux
étoiles ont des magnitudes qui diffèrent de 1 lorsque le rapport entre leurs intensités lumineuses est de
2,512.
À l’œil nu, on observe les étoiles jusqu’à la magnitude 6.
La magnitude apparente fait référence à l’énergie lumineuse reçue sur Terre (onnéglige le fait que si deux
étoiles sont identiques, la plus proche semble la plus brillante).
La magnitude absolue est calculée comme si toutes les étoiles se trouvaient à 10 parsec (32,6 années de
lumière).
Une lentille de Barlow est un système divergent qui permet de doubler la distance focale du miroir principal.
Pour pointer dans n’importe quelle direction du ciel, il faut 2 axes.
La monture azimutale comporte un axe vers le zénith et l’autre dans le plan horizontal (petites lunettes et
télescopes).
La monture équatoriale comporte un axe vers le pôle céleste (axe polaire) et l’autre dans le plan de l’équateur
céleste (axe de déclinaison). Cette monture nécessite un contrepoids.
Le chercheur est une petite lunette qui permet la recherche de l’astre que l’on veut observer ; ici, elle grossit
de 5 fois et le diamètre de l’objectif est de 24mm.
2. L’ouverture relative est le rapport F/D soit 1000/114 voisin de 9.
3. L’angle sous lequel est vu l’objet est de 1,1” cela correspond à 5,3×10−6rad. Le détail le plus fin visible
sur la Lune sera donc L=5,3×10−6×384 400 km =2 km environ.
4. La lumière est collectée par le télescope sur une surface de πD2/4. L’œil utilise une surface de π(6)2/4.
Si on suppose que l’œil est placé au centre oculaire, il reçoit toute la lumière collectée soit un rapport de
1142/62=361.
5. Grossissements : en utilisant le rapport des focales miroir principal/oculaire et en tenant compte d’une
part de la lentille de Barlow qui permet de multiplier par 2 les grossissements et de la limite pratique de
285, on retrouve bien les grossissements fournis.
2

EXERCICES SUR LE TÉLESCOPE 3
schémas sur le télescope
!"#$%&%$'()*+,*$'+,(#-.,
!"#"!!""#$%#&'()*+ !,-./!010
!"#
$%&'()*+,)%-.&"/-.,'(0*1%20.&0.304,%-
!5
65
7
8
9#
!
#
!"#$%&'(&'')"*$'(+(,-&".*/*.$(01213"*"14('53(,1(.$,1'")61
:%-*,;/1,)%-.&0.(")<+=0.&'>)-),)?0.&%--'0.2+;.(0.,'(0*1%20
9"
!"#
!5
65
7
8#
9#
!
!"5
!"85
95
!"
8"
!"#$%&%$'()*+,*$'+,(#-.,
!"#"!!""#$%#&'()*+ !,-./!010
!"#
$%&'()*+,)%-.&"/-.,'(0*1%20.&0.304,%-
!5
65
7
8
9#
!
#
!"#$%&'(&'')"*$'(+(,-&".*/*.$(01213"*"14('53(,1(.$,1'")61
:%-*,;/1,)%-.&0.(")<+=0.&'>)-),)?0.&%--'0.2+;.(0.,'(0*1%20
9"
!"#
!5
65
7
8#
9#
!
!"5
!"85
95
!"
8"
3