PDSB 2010/2011 TD n°1

p.1
PDSB 2010/2011 TD n°1
(Extraits de “Mechanics of motor proteins and the cytoskeleton ” de J. Howard, Sinauer, 2000
et de “ Random walks in Biology ”, H.C. Berg, Princeton University Press, 1993, “Physical
Biology of the Cell”, Phillips, Kondev, Theriot, Garland Science, 2008)
1. Efficacité du mécanisme de transport par diffusion.
On considère trois types d’objets en suspension dans l’eau :
• ion de potassium K
+
avec un coefficient de diffusion D ~ 2 10
-9
m
2
/s ;
• une protéine de masse moléculaire M
mol
=100 kDa ;
• une organelle de diamètre d=1 µm.
En sachant que :
1. la viscosité de l’eau est 0.9 mPa.s environ ;
2. la température de l’eau est 37 °C ;
3. la densité de la protéine est de 1.30 10
3
Kg/m
3
environ ;
4. la protéine et l’organelle ont une forme proche de la sphère ;
calculer :
A. le rayon (hydrodynamique) du ion de potassium ;
B. le rayon équivalent de la protéine ainsi que son coefficient de diffusion ;
C. le coefficient de diffusion de l’organelle.
On se demande de quantifier le transport induit par le phénomène de la diffusion pour ces
trois objets.
D. Pour donner une estimation de cela, calculer le temps nécessaire pour diffuser
sur des distances croissantes pour chaque objet: 1µm, 100 µm, 10 mm, 1 m.
E. Quel type d’information déduit-on par rapport de la diffusion comme mécanisme
de transport?
F. Et au niveau de la diffusion dans le cytoplasme d’une cellule?
G. Quelle autre stratégie de transport peut utiliser une cellule ?
2. Rôle du poids et de l’inertie en biologie cellulaire
Toujours pour une protéine de M
mol
= 100 kDa, calculer :
A. son poids en sachant que la force gravitationnelle se calcule comme F
grav
= M
prot
g,
où g=9,8 m/s
2
. (Rq : ne pas confondre la M
mol
avec la masse en kg !).
B. par conséquent, quelles stratégies pouvons nous utiliser pour séparer des
protéines en utilisant leur différence en masse ?
L’inertie est un phénomène dont on s’aperçoit facilement dans la vie quotidienne (ex. : force
centrifuge, quand on accélère ou on freine en voiture, … ). On se pose la question si l’inertie
est importante pour un objet de taille microscopique ou même nanoscopique. Pour répondre à
cela, on considère les cas d’une sphère de la taille typique d’une protéine, de masse M
mol
=
100 kDa et de rayon r=3 nm, et celle de la taille typique d’une bactérie (supposée spherique),
de masse M=4 10
-15
kg et de rayon r= 1µm.
En sachant que le temps caractéristique pour s’arrêter dans un milieu aqueux s’estime par la
relation M/ξ, où M est la masse de l’objet et ξ est le coefficient de frottement dans l’eau:
A. Vérifier que l’expression M/ξ
ξξ
ξ a bien la dimension physique d’un temps.
B. Si la vitesse thermique typique de la protéine est de 8,6 m/s et la vitesse typique
de la bactérie est de 25 µm/s, déterminer la respective distance caractéristique

p.2
pour s’arrêter.
C. Que déduisez vous à propos de l’inertie à cette échelle spatiale (nanométrique ou
micrométrique)?
3. Le mouvement de diffusion biaisée de la bactérie E.Coli
La bactérie E.Coli bouge dans un gradient de molécules attractantes ou répulsives par un
processus de diffusion biaisée. En absence de ces types de molécules, la bactérie alterne des
périodes de “ nage dirigée ”, c.a.d. en direction constante, (“ running ” en anglais) de la durée
de 1 s environ à des périodes de “ stationnement ” (“ tumbling ” en anglais) pendant lesquelles
la bactérie ne bouge sauf que par un mouvement rotatoire de diffusion (diffusion de rotation)
de la durée de 0,1 s environ. Pendant le “ stationnement ” la bactérie perd la direction de la
phase de nage précédente à cause du mouvement rotatoire de diffusion.
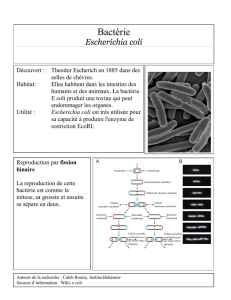
Le mouvement résultant a des propriétés similaires à celles d’un mouvement brownien (voir
figure).
Si la vitesse dirigée de la bactérie est de 30 µm/s, estimer son coefficient de diffusion de
translation efficace.
A voir http://www.aip.org/pt/jan00/berg.htm. (H.C. Berg, Physics Today, 53 (2000) , 24).
1
3
Figure 1: Trajectoire de E. Coli (depuis Berg '93)
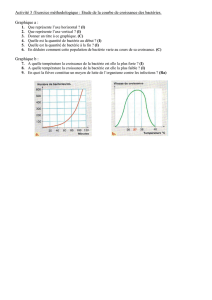
Figure 2: Mechanisme de nage de E. Coli (depuis Phillips et al., '08)
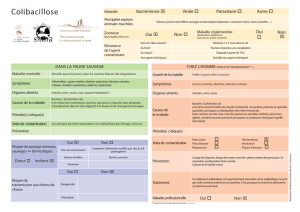
Figure 3: Section du moteur (depuis Nelson '04)
2