Points essentiels Pouvoir de résolution Le critère de Rayleigh

8/10/10%
1%
1
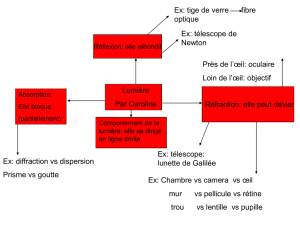
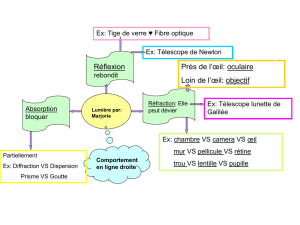
Points essentiels
 Diffraction à l’infini pour une ouverture circulaire
 Pouvoir de résolution et le critère de Rayleigh
 Pouvoir de résolution de l’œil
 Pouvoir de résolution d’un télescope
 Pouvoir de résolution pour un microscope
2
Diffraction pour une
ouverture circulaire
 Le premier minimum
apparaît lorsque:
 où a est le diamètre de
l’ouverture.
3
sin θ =1, 22
λ
a
Pouvoir de résolution
 En passant par un système
optique, les fronts d’onde
plane subissent une
diffraction. L’image d’une
source ponctuelle n’est
donc pas un point mais
une figure de diffraction.
Le pouvoir de résolution
d’un système optique,
c’est-à-dire sa capacité à
produire des images
nettes, est limité par la
diffraction.
4
Deux sources ponctuelles non cohérentes
peuvent être séparées si leurs figures de
diffraction ne se chevauchent pas.
Le critère de Rayleigh
 Selon le critère de
Rayleigh, deux images
sont tout juste séparées
lorsque le maximum
central d’une figure
coïncide avec le premier
minimum de l’autre. La
séparation angulaire
critique entre deux
sources, correspondant au
critère de Rayleigh s’écrit:
5
θ
c=1, 22
λ
a
Lord Rayleigh (1842-1919)
Pouvoir de résolution et
critère de Rayleigh
6

8/10/10%
2%
Illustration du critère de
Rayleigh
7
Pouvoir de
résolution de
l’œil
Calculez l’angle limite de résolution
de l’œil, en supposant que la pupille
ait un diamètre de 2,00 mm, pour
une longueur d’onde de 500 nm dans
l’air.
8
θ
min =1,22
λ
D
=1,22 ×500 ×10−9m
2×10−3m
=3×10−4rad ≈1 minute d'arc
Pouvoir de
résolution de
l’œil (suite)
Déterminez la séparation minimale d
entre deux sources ponctuelles que
l’œil est capable de distinguer si elles
sont situées à la distance L de
l’observateur.
9
Puisque θ
min est petit, sin
θ ~ tan θ !!
Alors d = L θ
min
Par exemple, si les objets sont placés à une distance de 25,0 cm de l’œil (p.p.), alors
d = 8 x 10-3 cm (environ l’épaisseur d’un cheveu)
Pouvoir de
résolution d’un
télescope
Le télescope Keck à Mauna Kea
(Hawaii), possède un diamètre
effectif de 10m. Calculez l’angle
limite de résolution pour une
longueur d’onde de 600 nm.
10
θ
min =1,22
λ
D
=1,22 ×600 ×10−9m
10 m
=7,3 ×10−8rad ≈0,015 seconde d'arc
Pouvoir de résolution d’un
télescope
11
La résolution des images formées par les télescopes terrestres
est limitée par l’atmosphère (et la pollution).
Le télescope
spatial
Calculez le pouvoir de résolution du
télescope spatial Hubble qui possède
un diamètre de 2,40 m . Utilisez une
longueur d’onde de 600 nm.
12
θ
min =1,22
λ
D
=1,22 ×600 ×10−9m
2,40 m
=3,05 ×10−7rad
Déterminez le plus petit cratère lunaire pouvant être résolu par ce télescope
(prendre une distance de 3,84 x 108 m).
Réponse: 117 mètres

8/10/10%
3%
Pouvoir de résolution d’un
microscope
13
Déterminez la plus petite distance d tout
juste résoluble par un microscope.
d=
1,22 λ ×fobj
D
où D est le diamètre de l’objectif.
Pouvoir de résolution d’un
microscope
14
Déterminez le pouvoir de résolution d’un microscope qui possède un objectif
de 9 mm (prendre λ =589 nm).
θ
min =1,22
λ
D
=1,22 ×589 ×10−9m
9×10−3 m
=7,98 ×10−5rad
En utilisant de la lumière visible, quel est le pouvoir de résolution maximal de ce
microscope?
Avec λ = 400 nm, on trouve 5,42 x 10-5 rad
Le microscope à immersion
15
θ
min =1,22
λ
D
=1,22 ×589 ×10−9m
n×9×10−3 m
Si on immerge l’objet et la surface avant de l’objectif dans l’huile, alors λn =
λ/n (microscope à immersion), on peut augmenter le pouvoir de séparation
d’un microscope.
Travail personnel
 Faire l’exemple 7,3
 Aucune question
 Solutionner les exercices: 11, 13 et 15
 Aucun problème
16