entilles minces - Jean

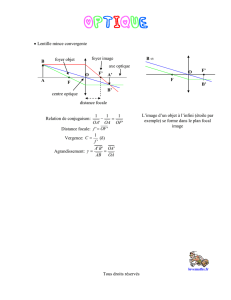
Lentilles
I77. Phare.
Un phare est constitué par un filament lumineux de 1 cm de long et par une lentille de diamètre 2 cm. Lorsque celle-
ci est à 11 cm du filament, elle en donne une image nette sur un écran situé à 110 cm de la lentille.
1) Quelle est la taille de cette image ?
2) Quelle est la distance focale de la lentille ?
3) Le filament étant à 10 cm de la lentille, quelle est la taille de la région éclairée à 100 mètres de la lentille ?
DS : lentilles, page 1
II64. Lunette.
Une lunette est constituée d’un objectif de
distance focale f1’ = 30 cm et de rayon r1 = 4 cm ,
d’un diaphragme de rayon r = 1 cm qui ne laisse
passer que les rayons situés à son niveau à moins de
1 cm de son axe et d’un oculaire de distance focale
f2’ = 2 cm. La distance entre le diaphragme et
l’objectif est 30 cm et celle entre le diaphragme et
l’oculaire est 2 cm. L’objectif, le diaphragme et l’oculaire ont même axe.
30 cm 2 c
m
1) Une étoile envoie des rayons parallèles entre eux et inclinés sur l’axe d’un angle α = 0,001 radian. En quel point
(position longitudinale et transversale) se forme l’image que donne l’objectif de cette étoile ?
2) Déterminer l’image que donne la lunette de l’étoile.
3) On appelle grossissement le rapport des angles sous lequel on voit un objet à travers l’instrument et à l’œil nu.
Quel est le grossissement de la lunette ?
4) En raison du diaphragme, seules sont visibles à travers la lunette les étoiles dont la direction fait avec l’axe un
angle borné par β. Calculer β.
5) On regarde dans la lunette à l’envers. Que devient le grossissement ?
6) Où se trouve le cercle oculaire, c’est-à-dire l’image que l’oculaire donne de l’objectif ? Quel est son rayon ?
7) On veut que la lunette donne d’un objet situé à 10,3 m de l’objectif une image à l’infini. Quel est le sens et la
grandeur du déplacement de l’oculaire nécessaire ?
8) Dessiner la marche du faisceau de rayons venant de l’étoile située dans une direction inclinée sur l’axe de l’angle
β. En déduire le rayon minimum de l’oculaire pour que celui-ci ne gêne pas la vision.
III50. Lunette.
Une lunette est constituée d’un objectif formé par une lentille mince convergente L1, de distance focale f’1 = 10 cm et
de diamètre d’ouverture d1 = 3 cm, et d’un oculaire formé par une lentille mince convergente L2, de distance focale
f’2 = 2 cm et de diamètre d’ouverture d2 = 1 cm. La distance entre L1 et L2 est réglable. Le lunette est réglée de façon à
donner d’un objet à l’infini une image à l’infini.
1) Calculer la distance L entre les deux lentilles.
2) Soit un objet AB frontal à distance finie. On appelle A1B1 l’image qu’en donne l’objectif et A’B’ l’image qu’en
donne le viseur. Calculer le grandissement ''AB
AB
γ=.
3) Si A se déplace de , son image A’ se déplace de . Calculer le grandissement axial de la lunette, c’est-à-
dire
A∆'A∆
'A
gA
∆
=∆. Pour trouver la relation entre A et A’, on pourra utiliser les formules de Newton.
4) Soit un objet à l’infini dans une direction faisant l’angle α avec l’axe ; son image est à l’infini dans une direction
faisant l’angle avec l’axe. Calculer le grossissement 'α'
G.
α
=α
5) Comme les rayons lumineux sont obligés de traverser l’objectif, ils sont obligés, après avoir traversé l’oculaire, de
passer par l’image que l’oculaire donne de l’objectif, qu’on appelle cercle oculaire. Déterminer la position du centre C
du cercle oculaire.
6) Déterminer le diamètre dC du cercle oculaire.
7) Dessiner avec soin la marche d’un faisceau lumineux arrivant parallèle sur l’objectif, incliné alors d’un angle α
sur l’axe et éclairant tout l’objectif. Pour cela, représenter les rayons extrêmes de ce faisceau et hachurer la région où il
y a de la lumière.
IV35. Viseur.
1) Un viseur est constitué d’un objectif formé par une lentille mince convergente L1, de distance focale f’1 = 10 cm et
de diamètre d’ouverture d1 = 3 cm, et d’un oculaire formé par une lentille mince convergente L2, de distance focale
f’2 = 2 cm et de diamètre d’ouverture d2 = 1 cm. La distance entre L1 et L2 est réglable. Le viseur est réglé de façon que
ce viseur donne d’un objet réel situé à 20 cm de l’objectif une image à l’infini. Quelle est la distance L entre L1 et L2 ?

2) Un objet AB situé à 20 cm de l’objectif est vu sous l’angle à travers le viseur. Calculer la puissance du viseur 'α
'
PAB
α
= en dioptries.
3) Comme les rayons lumineux sont obligés de traverser l’objectif, ils sont obligés, après avoir traversé l’oculaire, de
passer par l’image que l’oculaire donne de l’objectif, qu’on appelle cercle oculaire. Déterminer la position du centre C
du cercle oculaire.
4) En accommodant, l’observateur peut voir net des objets situés à une distance de lui comprise entre δ = 12,5 cm et
l’infini. Dans quelle région doit se trouver un objet pour que l’œil placé en C puisse le voir net à travers le viseur en
accommodant, C étant l’image que l’oculaire donne du centre optique de l’objectif ?
V59. Correction de la vue par une lentille.
1) On modélise un œil myope par une lentille mince, le cristallin, placée à la distance d = 23 mm d’un écran, la
rétine. Cet œil est capable de voir nets les objets situés à une distance comprise entre ∆ = 1 mètre et δ = 0,1 mètre en
faisant varier la vergence du cristallin. Dans quel intervalle peut-il la faire varier ?
2) Quelle lentille faut-il accoler à l’œil pour qu’il soit capable, en accommodant, de voir nets les objets entre l’infini
et la distance la plus courte possible ? Quelle est cette dernière distance ?
VI91. Mesure de distance focale d’une lentille.
1) Pour mesurer la distance focale 1
f
′ d'une lentille convergente, l'on forme avec cette lentille sur un écran l'image
d'un objet transversal de longueur 20 mm. Lorsque cette image, renversée, mesure aussi 20 mm, la distance entre l'objet
et l'image est d = 124 cm. Déterminer 1
f
′.
2) On accole à cette lentille une autre lentille. Lorsque l'image, renversée, du même objet mesure 20 mm, sa distance
à l'objet est d’ = 248 cm. Quelle est la distance focale 2
f
′ de la seconde lentille ?
VII75. Appareil photographique.
Un appareil photographique est constitué d'une lentille mince de vergence +20 dioptries qui donne sur la pellicule
une image nette de l'objet photographié.
1) Quelle est la distance entre l'objectif et la pellicule pour photographier une montagne de 500 m de haut située à 10
km ?
2) Quelle est la taille de l'image de la montagne sur la pellicule ?
3) Quelle est la distance entre l'objectif et la pellicule pour photographier une fleur de 0,1 m de haut située à 1 m de
l’objectif ?
4) Quelle est la taille de l'image de la fleur sur la pellicule ?
5) On appelle tirage la distance dont on a déplacé l'objectif par rapport à la pellicule par rapport au cas de la mise au
point sur un objet à l’infini. Calculer le tirage lors de la photographie de la fleur.
6) Le tirage peut varier entre zéro et cette valeur. Dans quel intervalle peut varier la distance entre un objet à
photographier et l’objectif pour que la mise au point soit possible ?
7) On accole à l'objectif une bonnette, constituée par une lentille de vergence + 2 dioptries. A quelle distance de
l'objectif faut-il que se trouve la fleur photographiée nette lorsque la distance entre l'objectif et la pellicule est celle de la
question 1) ?
8) Quelle est alors la taille de son image sur la pellicule ?
9) A quelle distance de l'objectif faut-il que se trouve la fleur photographiée nette lorsque la distance entre l'objectif
et la pellicule est celle de la question 3) ?
10) Dans quel cas, avec ou sans bonnette, la mise au point doit-elle être la plus précise ?
11) On appelle amplitude dioptrique la variation de l'inverse de la distance entre l'objet photographié et l'objectif
quand on fait varier la distance entre la pellicule et l'objectif. Montrer que la bonnette ne modifie pas l'amplitude
dioptrique.
12) Dans des bonnes conditions d'éclairage, l'œil ne peut séparer deux détails que s'il les voit sous un angle supérieur
à α = 3.10–4 radian . Quelle est la taille du plus petit détail qu'il peut discerner sur une photographie située à 25 cm de
son œil ?
13) Même question en regardant la photographie à travers une lentille de vergence +50 dioptries placée à 2 cm
d'elle ?
VIII52. Lunette astronomique.
On observe deux étoiles et à l’aide d’une lunette astronomique et d’un détecteur. Les deux étoiles et
sont considérées ponctuelles et à l’infini, séparées par une distance angulaire θ , l’étoile étant située dans la
direction de l’axe optique de la lunette.
a
Eb Ea Eb E
a
E
La lunette astronomique d’axe optique zz (Figure 1) est constituée d’un objectif assimilé à une lentille mince
convergente de diamètre et de distance focale image
′
1
L150 cmD=17, 5 m
f
′= associé à une lentille divergente
de distance focale image
2
L
20, 025 m
f
′=− . On désigne respectivement par et , par et , et , les
centres optiques, les foyers objet et image des lentilles et . 1
O2 O1 F1 F′2 F2 F′
1
L2 L
DS : lentilles, page 2

1. Quelle est la forme et la direction des faisceaux lumineux des ondes 1 et 2, respectivement émises par les étoiles
et , lorsqu’elles parviennent sur la lunette ?
a
Eb E
2. On appelle l’image de l’étoile à travers la lentille . De même, désigne l’image de à travers .
1
Aa E1 L1 Bb E1 L
a) Dans quel plan se situent et ? Donner la distance algébrique
1
A1 B11 AB .
b) La lentille est placée peu avant le plan où se forment les images et . On appelle respectivement et
les images de et à travers la lunette. Sachant que
2
L1 A1 B2 A
2
Ba Eb E22
11
2
AB
AB =, exprimer et calculer la distance 21
OA .
3. On définit la distance focale
f
′ de la lunette par la relation 22
AB f′
=θ.
a) Calculer la distance focale
f
′ de la lunette.
b) Calculer 12 AA .
c) Quel est l’intérêt d’ajouter la lentille ? Quel est son inconvénient ?
2
L
4. On place dans le plan où se forment les images et , une caméra à DTC (Dispositif à Transfert de Charge).
Ce récepteur d’images est composé d’une matrice rectangulaire de 768 détecteurs élémentaires, appelés pixels,
de forme carrée, de côtés . On suppose que la lunette est librement orientable.
2
A2 B
512×
19ma=µ
Une image parfaite à travers la lunette d’un point situé à l’infini, produit sur le détecteur un signal donnant une image
dont la dimension ne peut être inférieure à la taille d’un pixel.
Exprimer et calculer en seconde d’arc, la limite de séparation angulaire de deux étoiles due au récepteur
d’image. Quelle est la plus grande valeur de séparation angulaire décelable de deux étoiles en minute d’arc ?
min
θ
max
θ
IX22. Microscope.
Un microscope porte les indications suivantes : sur son objectif : x40 ; sur son oculaire: x10. La notice du
constructeur précise : ouverture numérique de l'objectif , intervalle optique . La signification de
ces indications sera précisée dans la suite. On modélise ce microscope par deux lentilles minces convergentes,
l’objectif, de centre optique et de foyers et , et l’oculaire, de centre optique et de foyers et .
L’intervalle optique
00, 65ω=16 cm∆=
1
O1 F1 F′2 O2 F2 F′
12
FF
′
∆= est positif, c’est-à-dire dans le sens de propagation de la lumière.
Soit un objet réel AB, perpendiculaire à l'axe optique, A étant sur l'axe, un peu plus loin de l'objectif que le foyer
objet de cet objectif ; l’objectif donne de AB une image intermédiaire A1B1 ; l’oculaire donne de A1B1 une image A'B'.
Nous supposerons cette image à l’infini. Elle est observée par un œil situé au voisinage du foyer image de l'oculaire. Cet
œil est dit emmétrope, car il est capable d’accommoder pour voir nets les objets situés entre la distance et
l'infini. 25 cmδ=
1) Faire un schéma qualitatif du dispositif, sans chercher à respecter les proportions entre les longueurs données par
l’énoncé, et tracer la marche de deux rayons lumineux issus du point B, l'un émis parallèlement à l'axe optique, l'autre
passant par .
1
F
2) L'indication portée sur l'oculaire (x10) est le grossissement commercial de l’oculaire, c’est-à-dire le
rapport de l'angle sous lequel on voit l'image à l'infini d'un objet à travers l'oculaire seul (et non à travers le
microscope) et de l'angle α sous lequel on voit ce même objet à l'œil nu lorsqu'il est situé à la distance minimale de
vision distincte. Déterminer
210G=
′
α
2
f
′, distance focale image de l'oculaire.
3) L'indication portée sur l'objectif (x40) est la valeur absolue du grandissement 111
/AB ABγ= de l'objectif :
140γ=. Calculer 1
f
′, distance focale image de la lentille équivalente à l'objectif .
4) Calculer la distance entre l'objet et l’objectif.
1
OA
5) Calculer la latitude de mise au point, c’est-à-dire la variation de la distance compatible avec une vision nette
de l'image finale par l'observateur, dont l'œil est au foyer image de l'oculaire. Interpréter le résultat obtenu.
1
OA
6) Calculer dans le cas d'une image finale à l'infini le grossissement commercial G du microscope.
DS : lentilles, page 3

7) L'ouverture numérique du microscope, , correspond à , n indice du milieu dans lequel plonge
l'objectif, angle maximum des rayons issus de A arrivant sur l'objectif. Calculer pour un objectif plongé dans l'air.
Le microscope est-il utilisé dans les conditions de Gauss ? Quel est l'ordre de grandeur du diamètre de la monture de
l'objectif ?
0
ωsinnu
u u
D
8) Déterminer la position C et le diamètre d du cercle oculaire, image de la monture de l'objectif à travers l'oculaire.
Quel est l'intérêt de placer l'œil sur le cercle oculaire ?
X42. L’objectif photographique.
Dans tout le problème, on supposera l'approximation de Gauss valable.
Les lentilles seront désignées par la lettre L, leurs foyers objet et image étant respectivement F et F', leur centre optique
O, leur distance focale image f'.
On notera A et A' respectivement, le couple de points conjugués objet et image.
1° Objectif simple.
Un objectif photographique est modélisé par une lentille mince de distance focale image f' = 50 mm. La mise au point
s'effectue en déplaçant l'objectif par rapport à la pellicule (P).
a. Où faut il placer la pellicule pour photographier un immeuble de 20 m de haut, situé à 1 km du centre O ? Calculer la
grandeur de son image. ''AB
b. Le tirage de l'appareil est la distance dont il faut déplacer l’objectif par rapport à la pellicule pour photographier un
objet à distance finie au lieu d’un objet à l’infini. Le tirage maximum permet de photographier un objet situé à
de l’objectif. Quel est ce tirage maximum ?
t
0, 9 mδ=
c. On suppose la mise au point faite sur l'infini.
L'objectif possède un diaphragme à iris d'ouverture réglable, placé contre la lentille. Son diamètre D s'exprime en
fonction de la distance focale f' et de l'ouverture n suivant la relation D = f’/n. La structure du film étant granulaire, la
tache image correspondant à un objet ponctuel a le diamètre d'un grain a = 25 µm = 25. 10–6 m. Déterminer l'ensemble
des positions d'un objet A sur l'axe optique donnant une image aussi nette que pour un point à l'infini.
Application numérique : Calculer la distance minimale de cet objet au centre optique, l'ouverture étant n = 16.
d. On appelle limite de résolution, la distance minimale de deux objets A et B dans un plan perpendiculaire à l'axe, dont
les images A' et B’ sont distinctes sur la pellicule. Cette distance A'B' doit être supérieure au grain de la pellicule a.
Déterminer cette limite en fonction de a, f',AF .
Application numérique : Comment placer l'objectif par rapport à A pour que cette limite de résolution soit la plus faible
possible. La calculer.
2° Téléobjectif.
Pour augmenter le grandissement de l'image et abaisser la limite de résolution, il faut utiliser des objectifs de grande
focale, ce qui conduit à des appareils encombrants et lourds.
On préfère utiliser deux lentilles, L1 convergente de distance focale f’1 = 50 mm et L2 divergente, placée derrière, de
distance focale f’2 = – 20 mm. La distance des centres optiques est O1O2 = 35 mm.
a. Calculer numériquement la position du foyer image F' du système, c’est-à-dire l’image du point à l’infini dans le
système.
b. Déterminer la grandeur de l'image de l'objet AB défini en 1° a.
c. Quelle serait la distance focale d'une lentille convergente unique donnant une image de même grandeur ? Intérêt du
dispositif ?
3° Aberration chromatique.
La vergence d’une lentille d’indice n et dont les faces ont pour sommets S1 et S2 et pour centres C1 et C2 est
11 22
11
(1)
Vn SC SC
⎛⎞
⎟
⎜⎟
=−−
⎜⎟
⎜⎟
⎟
⎜
⎝⎠
.
Pour corriger le chromatisme de l'objectif, on associe deux lentilles L1 et L2, respectivement
convergente et divergente.
DS : lentilles, page 4
Les centres optiques étant pratiquement confondus (lentilles accolées) :
L1 est d'un verre d'indice 11
111 1
21, 5 1 5 4, 5 . 1 0 m
B5-2
C B
λ
−
=+ = =
nC ;
L2 est d'un verre d'indice 21
222 2
21, 6 5 2 7, 4 . 1 0 m
B5-2
C B
λ
−
=+ = =
nC .

a. Donnez sans démonstration la vergence de la lentille unique équivalente en fonction de f'1 et f’2 ?
b. L1 est équiconvexe, ses rayons de courbure égaux ont pour valeur absolue R1. L2, accolée, a un rayon de courbure
arithmétique R1, sa face non accolée a un rayon de courbure algébrique R2. Calculer R1 et R2 pour que la lentille
équivalente ait une distance focale f' = 5 cm, indépendante de la longueur d'onde.
Réponses
I. 1) 10 cm ; 2) 10 cm
f
′= ; 3) . 10 mD′
α=
II. 1) dans le plan du diaphragme, à
0,3 mm de l’axe ; 2) à l’infini dans une
direction inclinée de 0,015 radian sur
l’axe ; 3) 1
2
15
f
G
f
′
==
′ ; 4)
1
0, 0333 rad
r
f
β==
′ ; 5) 15
1
=G ; 6)
2,133 cm derrière l’oculaire ; rayon
0,267 cm ; 7) reculer l’oculaire de 0,9
cm ; 8) .
2min 1, 3 3 c mr=
2 c
m
30 cm
III. 1) ; 2)
12
12 cmLf f
′′
=+= 2
1
0, 2
f
f
′
γ=−=−
′ ; 3)
2
2
2
1
0, 04
f
g
f
′
==
′ ; 4) 1
2
5
f
G
f
′
==
′ ; 5)
2
2
2
21
0, 4 cm
f
FC FO
′
−
′== ; 6) 12
1
0, 6 cm
C
df
d
f
′
==
′ ; 7) voir
ci-contre.
IV. 1) L = 2f1’ + f2’ = 22 cm ; 2)
2
150 dioptriesP
f
==
′ ;
3) 2
2
2
21
'
'0
f,2cm
FO
−
==FC ; 4) à une distance de l’objectif
du viseur comprise entre 19,685 et 20 cm.
Figure 3
r2,min
V. 1) entre 0
1144, 5 dioptriesV et
d
=+ =
∆1
1153, 5 dioptriesV ; 2) V ;
d
=+=
δ=−∆=−
21/ 1dioptrie
2
10, 111 m
1/V
′
δ==
+δ.
VI. 1) 31 cm
4
D
f′== ; 2) 262 cm
f
′=−.
VII. 1) 50 mm ; 2) 2, 5 mm
f
AB
AB ; 3)
D
′⋅
′′
== 15,263 mm
1/
pVp
′==
+ ; 4) ; 5)
; 6) entre l’infini et 1 m ; 7)
5, 26 mmAB
′′
=
2, 63 mm 10, 5 m
1/
ppV ==−
′−′′
= ; 8) AB ; 9) 10 mm
10, 333 m
1/
ppV ==−
′−; 10) avec la bonnette, la mise au point doit être plus précise ; 12)AB ;
13) AB .
75 m=δα =µ
f′ =α=µ6m
• VIII. 1) envoie un faisceau de rayons parallèles à l’axe ; envoie un faisceau de rayons parallèles entre eux
et faisant l’angle avec l’axe ; 2.a) et sont dans le plan focal image de L,
a
Eb E
θ1 A1 B1 1 7, 5 m
f
′= derrière cette lentille ;
11 1
AB f′ =θ ; 2.b) 21 O 0, 0125 mA= ; 3.a) 1 215m
f
f
′′
== ; 3.b) 12 0, 0125 mAA ; 3.c) L réduit la taille du
dispositif et le champ transversal ; 4) θ ;
=
==
2
min 2 2 / 0,124 secondeAB f′
722
max 6.10 768 512 1, 9 minute
−
θ=×+= .
IX. 1) voir ci-contre ; 2) 22
2, 5 cmfG
δ
′== ; 3)
11
0, 4 cmf∆
′==
γ ; 4) O0 ; 5) 1, ; 6)
1,41cmA=5 4 mµ
21 400GG=γ= ; 7) u ; conditions de Gauss 40,5
DS : lentilles, page 5
A
B
1
F′
1
F21
FA=
1
B
2
F′
=°