1 T.P-cours de Physique n°5 : LE TELESCOPE DE NEWTON 1

TS Spécialité-Optique instrument d’optique
1
F
1
Objectif constitué d’un
miroir sphérique concave
(miroir principal)
Oculaire
Miroir plan
(miroir secondaire)
F
2
,
1
F′
2
F′
T.P-cours de Physique n°5 : L E TELESCOPE DE N EWTON
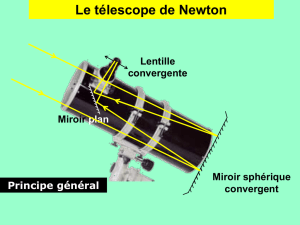
1. Utilité et description du télescope de Newton.
Pour remédier aux difficultés provoquées par l'utilisation des lentilles qui
composent la lunette astronomique, Newton les remplaça par des miroirs. Grâce
à ces miroirs, les performances du télescope sont bien supérieures à celles de
la lunette astronomique.
Le mot télescope est réservé aux instruments d'optique dont l'objectif est un
miroir concave.
Un télescope est donc formé principalement de deux systèmes optiques :
- Un miroir principal (parabolique ou sphérique) de grande distance
focale et de grand diamètre (ou ouverture) ;
- un oculaire de courte distance focale qui joue le
rôle de loupe.
Le miroir principal donne de l'objet ponctuel situé à l'infini, une
image ponctuelle située dans le plan focal du miroir, du même
côté du miroir que l'objet.
IL y a donc un problème pour l'observateur qui doit regarder
l'image à travers l'oculaire sans se placer entre l'objet et le
miroir principal. Il existe plusieurs solutions pour pallier cette
difficulté.
Dans le télescope de Newton,que nous allons étudier, un
miroir plan à 45° renvoie sur le côté les rayons lumineux.
L'image donnée par l'objectif peut ainsi être observée
latéralement.
Quelque soit le dispositif utilisé, une partie non négligeable de
la lumière qui pénètre dans le télescope est arrêtée par le miroir secondaire et le dispositif qui le maintient en place,
appelé araignée.
Un télescope est donc un entonnoir de lumière qui permet de donner une image rapprochée d’objets lointains
de grandes dimensions.
Marche simplifiée des rayons lumineux à travers un télescope de Newton afocal (l’image à travers l’instrument d’un
objet situé à l’infini est à l’infini).
2- Modélisation d’un télescope de Newton.
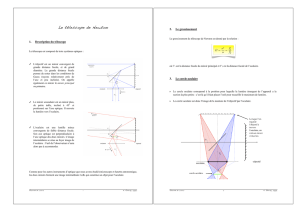
On observe à l’aide d’un télescope de Newton, un objet plan AB très éloigné. Les rayons issus de l’objet font un angle
θ avec l’axe optique du miroir principal. (construction n°1)
Télescope de Newton 114/900
C
oupe
schématique d’un télescope de Newton
Partie A :
Produire des
images et
observer

TS Spécialité-Optique instrument d’optique
2
2-1 Étude de l’objectif (miroir principal).
1. Quel est le rayon de courbure R du miroir sphérique du document ci-joint (à l’échelle 1/1) ?
2. Construire sur le schéma l’image A
1
B
1
donnée par le miroir sphérique (objectif) d’un objet AB situé à
l’infini. Quelle est la nature de l’image obtenue ?
3. Quel est donc le rôle de l’objectif ?
2-2 Rôle du miroir plan (ou miroir secondaire).
L’image A
1
B
1
joue le rôle ………………………….. pour le miroir plan.
4. Quelle est la particularité de l’image A
2
B
2
donnée par le miroir plan de l’objet A
1
B
1
?
5. Construire cette image (construction n°2).
2-3 Rôle de l’oculaire.
L’image A
2
B
2
joue le rôle ………………………….. pour l’oculaire modélisé par une lentille convergente.
6. Où doit se former l’image définitive A’B’ pour qu’un œil « normal » qui l’observe n’est pas à
accommoder ?
7. Où doit donc se former l’image A
2
B
2
donnée par le miroir plan ? Positionner le foyer objet F
2
et image
F
2
’ de l’oculaire dans cette configuration.
8. Construire l’image définitive A’B’ (construction n°3).
2-4 Grossissement du télescope.
Le grossissement G du télescope est définit par la relation :
θ
θ
=' G , où : θ’ est l’angle sous lequel est vu
l'image définitive de l'objet à travers le télescope (c’est le diamètre apparent de l’image définitive à travers
le système optique) et θ l’angle sous lequel est vu l'objet à l'œil nu (c’est-à-dire le diamètre apparent de
l’objet).
9. À l’aide de la construction précédente, exprimer le diamètre apparent θ de l’objet à l’œil nu.
10. Exprimer également le diamètre apparent θ’ de l’objet observé à travers le télescope.
11. En déduire le grossissement du télescope de newton en fonction de ses caractéristiques.
12. Calculer la valeur du grossissement du télescope du document.
3 -Exercice : extraits de la notice d’un télescope.
Caractéristiques :
Télescope 114/900
Référence : T41
Télescope Newton à miroir alumine, sur monture
équatoriale pour toutes observations : lunaires,
planétaires, stellaires.
Diamètre 114 mm ; Focale 900 mm
Deux oculaires: 6 mm et 20 mm
Grossissements 45×, 150×,
Monture équatoriale avec flexibles, motorisable, trépied
aluminium.
Comment ça marche ?
Le télescope est un système optique conçu pour
l'observation des astres. Le télescope que vous avez
acheté s'appelle un télescope réflecteur type Newton.
C'est un tube ouvert à une extrémité avec un miroir
courbe à l'autre.
Les rayons lumineux rentrent par l'extrémité ouverte du
tube et viennent frapper le miroir courbe appelé "miroir principal".
Les rayons réfléchis par ce miroir viennent ensuite en frapper un second, appelé " miroir diagonal" (miroir secondaire)
Ce petit miroir plan, placé au centre du tube à 45 degrés, renvoie l'image formée par le miroir principal, sur le côté où
on l'observe avec l'oculaire qui joue le rôle de loupe.
Par suite de la courbure du miroir principal, les rayons de lumière sont courbés pour se concentrer en un point. Le
miroir principal d'un télescope doit être poli exactement selon la courbure appropriée afin de garantir le point focal
correct. Il est très important que les deux miroirs soient dans le bon alignement pour obtenir les meilleurs résultats.
(A vérifier régulièrement). Ce télescope est muni d'une monture équatoriale qui permet le déplacement du tube et
donc l'observation d'un astre dans toutes les directions.

TS Spécialité-Optique instrument d’optique
3
Partie A : Questions sur la notice
A.1. Nommer sur votre copie les éléments optiques légendés 1, 2, 3 sur le schéma de la notice.
A.2. Que signifient les indications : Diamètre 114 mm, Focale 900 mm ?
A.3. Quel est le nom de la grandeur dont on donne la valeur en mm avec chaque oculaire ?
A.4. Dans la phrase suivante". Par suite de la courbure du miroir principal, les rayons de lumière sont courbés pour
se concentrer en un point "
A.4.1. Que représente ce point pour le miroir principal ?
A.4.2. Le mot « courbés » employé à propos des rayons lumineux est impropre. Expliquer ce que veut dire
l'auteur de la notice en l'utilisant.
Partie B : Analyse du fonctionnement
Modélisation du télescope de Newton : les notations utilisées dans les questions suivantes font référence au schéma de
la feuille annexe à consulter, à compléter et à remettre avec la copie. Ce schéma ne respecte pas les dimensions.
Dans tout l'exercice, nous modéliserons :
− le miroir principal par un miroir sphérique de sommet S et de foyer F'
1
;
− l'oculaire par une lentille mince convergente de centre optique O
2
et de focale f ’
2
et dont l'axe optique est
perpendiculaire à celui du miroir principal;
− le miroir secondaire par un miroir plan dont le milieu M est placé sur l'axe optique du miroir principal et sur
l'axe optique de l'oculaire.
B.1. Formation des images.
Le télescope est pointé vers un astre. On assimilera l'astre à un objet (AB), situé à l'infini
et vu sous l'angle apparent θ, le point A étant situé sur l'axe du miroir principal. Le miroir principal donne de
l'objet (AB) une image (A
1
B
1
).
B.1.1. Dans le télescope "114/900", quelle est la valeur de la distance A
1
S ? Justifier brièvement.
B.1.2. (A
1
B
1
) joue le rôle d'objet pour le miroir secondaire qui en donne une image (A
2
B
2
). Construire sur le
schéma de la feuille annexe à remettre avec la copie, l'image (A
2
B
2
). Justifier brièvement.
(A
2
B
2
) est examinée à travers l'oculaire qui en donne une image définitive (A'B’) à l'infini.
B.1.3. Placer les foyers image F'
2
et objet F
2
de l'oculaire pour que l'image définitive soit rejetée à l'infini.
B.1.4. Construire deux rayons émergents de l'oculaire et issus de B
2
.
B.1.5. Construire, à travers la totalité de l'instrument, la marche du faisceau lumineux issu de B et limité par
les deux rayons incidents fléchés.
B.2. Grossissement.
L'observateur qui regarde dans le télescope voit l'image définitive sous l'angle θ'. On définit le grossissement
dans le cas d'une vision à l'infini
θ
θ
=' G ; θ et θ' sont exprimés en radian.
B.2.1. Établir que G est aussi égal au quotient de la distance focale du miroir principal par celle de l'oculaire
(les angles sont petits : sinθ ≈ tan θ ≈ θ (rad)).
B.2.2. Quel oculaire doit-on choisir pour que le grossissement soit 150× ?