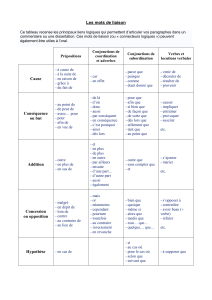
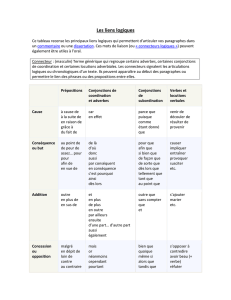
Résumé Systèmes Logiques : Algèbre de Boole, Portes, MUX & DEMUX

■ Résumé Total - Systèmes Logiques
Étudiante : Arij Hamraoui - ISET Charguia
1■■ ALGÈBRE DE BOOLE
L’algèbre de Boole est un système mathématique binaire utilisé pour modéliser les circuits
logiques numériques. Elle manipule des variables logiques (0 ou 1) et des opérateurs de
base : ET (AND), OU (OR) et NON (NOT).
Opération Nom Symbole Expression Sortie = 1 si...
ET AND . A.B A=1 et B=1
OU OR + A+B A=1 ou B=1
NON NOT ¯ A' A=0
NAND NON-ET &o (A.B)' au moins un 0
NOR NON-OU ≥1o (A+B)' tous 0
XOR OU exclusif ⊕A'B + AB' A ≠ B
XNOR Équivalence ■AB + A'B' A = B
2■■ PROPRIÉTÉS ET LOIS DE BASE
Idempotence A + A = A ; A.A = A
Commutativité A + B = B + A ; A.B = B.A
Associativité (A + B) + C = A + (B + C)
Distributivité A.(B + C) = A.B + A.C
Complémentarité A + A' = 1 ; A.A' = 0
Identité A + 0 = A ; A.1 = A
Négation (A')' = A
Absorption A + A.B = A ; A.(A + B) = A
De Morgan (A.B)' = A' + B' ; (A + B)' = A'.B'
3■■ REPRÉSENTATION ET SIMPLIFICATION
Une fonction logique peut être représentée sous forme algébrique, par table de vérité ou
par schéma (logigramme). La simplification vise à réduire le nombre de termes ou de
portes logiques nécessaires.
Méthodes de simplification : • Simplification algébrique (via les lois de Boole) • Table de
Karnaugh : représentation graphique pour regrouper les 1 adjacents et minimiser les
termes.
Exemple : F(A,B,C) = Σ(1,2,3,7) → F = B'C + A.B
4■■ PORTES LOGIQUES

Porte Symbole Expression Utilité
NON ■o Y = A' Inverse une entrée
ET & Y = A.B Sortie 1 si toutes les entrées sont 1
OU ≥1 Y = A + B Sortie 1 si au moins une entrée est 1
NAND &o Y = (A.B)' Porte universelle
NOR ≥1o Y = (A+B)' Porte universelle
XOR ⊕Y = A'B + AB' Détecteur de différence (parité impaire)
XNOR ■Y = AB + A'B' Détecteur d’égalité (parité paire)
5■■ MULTIPLEXEUR (MUX)
Le multiplexeur sélectionne une entrée parmi plusieurs pour la transmettre à une sortie
unique. C’est un sélecteur contrôlé par des bits d’adresse.
Pour un MUX à 2■ entrées, il faut n lignes de sélection. Exemple : MUX 4→1 → 4 entrées
(D0–D3), 2 sélections (S1,S0), 1 sortie Y.
Formule : Y = D0S1'S0' + D1S1'S0 + D2S1S0' + D3S1S0
Schéma logique simplifié : Entrées → [MUX] → Sortie ↑ Lignes de sélection (adresse)
Applications : • Transmission sélective de signaux • Réalisation de fonctions logiques à
partir de tables de vérité • Commutation dans les processeurs et systèmes de
communication.
6■■ DÉMULTIPLEXEUR (DEMUX)
Le démultiplexeur fait l’opération inverse du MUX. Il a une seule entrée et plusieurs
sorties. Selon les lignes de sélection, l’entrée est redirigée vers une sortie unique.
Exemple : DEMUX 1→4 → 1 entrée (E), 2 sélections (S1,S0), 4 sorties (Y0–Y3). Si
S1S0=00 → Y0=E ; S1S0=01 → Y1=E ; S1S0=10 → Y2=E ; S1S0=11 → Y3=E.
Applications : • Conversion série → parallèle • Contrôle d’affichage • Commutation de
signaux vers plusieurs destinations.
7■■ CODEUR ET DÉCODEUR
■ CODEUR :
Transforme un signal actif parmi plusieurs entrées en un code binaire compact. Exemple :
Codeur 8→3 → 8 entrées, 3 sorties binaires. D0→000 ; D1→001 ; … ; D7→111
Applications : claviers, systèmes de codage, transmission binaire.
■ DÉCODEUR :
Fait l’opération inverse : convertit un mot binaire en une sortie unique active. Exemple :
Décodeur 3→8 : 3 entrées, 8 sorties (une seule active selon le code binaire).
Applications : sélection de lignes mémoire, circuits logiques, affichages,
microprocesseurs.
■ FORMULES ESSENTIELLES À RETENIR

A + A' = 1 A.A' = 0
(A + B)' = A'.B' (A.B)' = A' + B'
A + AB = A A(A + B) = A
A ⊕ B = A'B + AB' A ■ B = AB + A'B'
A + 0 = A A.1 = A
A + 1 = 1 A.0 = 0
9■■ MÉTHODOLOGIE DE CONCEPTION D’UN CIRCUIT LOGIQUE
1. Établir la table de vérité. 2. Exprimer la fonction sous forme algébrique (SOP/POS). 3.
Simplifier la fonction (algébrique ou Karnaugh). 4. Réaliser le schéma logique. 5.
Implémenter avec des portes logiques, MUX, DEMUX, etc.