Exercícios de Eletricidade para Estudantes Universitários

Page 1 sur 7
UNB/ESI Année universitaire 2024-2025
TC1
Travaux dirigés D d’électricité
Exercice I.*
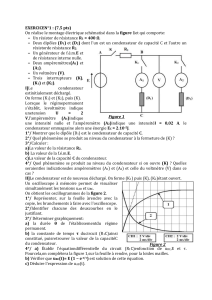
On considère les figures 1 et 2.
1) Calculer les tension V1, V2, V3, V4 et V5.
2) Déterminer la résistance équivalente entre A et B de la figure 2.
Figure 1
Figure 2 (NB : valeur des résistances en Ω)
3) Deux générateurs de résistances internes identiques, montés en série donnent une tension à
vide U10= 36V. Lorsqu’ils sont montés en opposition, cette tension devient U20=12V.
Calculer la f.é.m de chaque générateur.
Exercice II*:
En utilisant le pont diviseur de courant et celui de tension déterminé :
1) le courant traversant la résistance R1 de la figure 3,
2) la tension aux bornes de la résistance R4 de la figure 4.
3) La f.é.m E2 du montage de la figure 3,
4) Le courant I1 fourni par le générateur E1 (figure 4).
Ri=5i
((exemple R6=5x6
.=30
)
Figure 3
Ri=5i
; E1=10V
Figure 4
Exercice III :
Soit le circuit suivant (figure 5) avec :
E=12V; R1= 5Ω; R2=5Ω; C=47µF.
Quel doit être la valeur de R3 pour qu’au bout d’un temps t=5s la tension aux bornes du condensateur
soit Vc=6V ?
Dr. SAWADOGO Enseignant chercheur physicien

Page 2 sur 7
Figure 5
NB : Tension initiale du condensateur Vc=0V.
Exercice IV*
Soit le circuit de la figure 6 :
1) En utilisant les lois de Kirchhoff déterminer les intensités les courants I, I1, I2, I3 et I4.
2) Déterminer le générateur de Nothon vu des bornes A et B.
3) Déduire l’intensité du courant I4 qui traverse la résistance R
Figure 6
Exercice V* :
On réalise le montage de la figure 7. Les deux mailles contiennent deux bobines identiques de résistance R et de self
L. La branche AB a une résistance r. Toutes les autres résistances sont négligeables.
L’interrupteur K étant fermé, le régime permanent établi, évaluer les intensités dans les branches du réseau. Examiner le cas
particulier où r=0.
On considère le cas r=0 On laisse le courant circuler pendant un temps assez long, puis on ouvre l’interrupteur à l’instant
t=0.
1-) Trouver l’expression de l’intensité i(t) du courant traversant alors le générateur.
1-) Calculer numériquement i au bout de t=10-2s sachant que E=2V, R=5 L=0,1H.
Figure 7
Exercice VI* :
On charge un condensateur de capacité C initialement déchargé grâce à un générateur de f.é.m E (figure 8). On a
placé aux bornes du condensateur une dérivation de résistance R2.

Page 3 sur 7
Le circuit principal a une résistance totale R1 et une self négligeable. Déterminer les expressions en fonction du temps de la
tension v(t)=vA-vB aux bornes du condensateur, de la charge q(t) du condensateur et des intensités i1(t), i2(t) et i(t) dans les
branches du réseau.
Figure 8
Exercice VII*
Soit le circuit ci-contre (figure 9). :
1) Déterminer les expressions complexes des courants ,  , et 
2) Calculer les puissances actives (P), réactives (Q) et apparente (S) fournies par le générateur et celles consommée
dans les branches contenant l’inductance et le condensateur.
3) Déterminer les courants instantanés i(t), i1(t) et i2(t) qui circule en régime permanent.
 12
500cos210
tte
Figure 9
Exercice VIII :
Soit le réseau suivant :
figure 10
Figure 11
1)- Déterminer les résistances R1, R2 et R3 pour que les figures 10 et 11 soient équivalentes
2) - Calculer le courant I5 en appliquant les lois de KIRCHHOFF.
2°-Vérifier le résultat par application du théorème de superposition.
Exercice IX* :
Le circuit série de la figure 12 comportant les éléments : R=10Ω, L=0.2H et C=40mF est alimenté par une source de
tension de fréquence variable.

Page 4 sur 7
1) Déterminer les fréquences f1, f0 et f2 pour lesquelles le courant est respectivement en avance de 
 sur la tension,
en phase avec la tension, en retard de 
 sur la tension.
2) Quelle est la prédominance du circuit dans chaque cas ?
Figure 12
Exercice X* :
On considère le circuit de la figure 13.
1) En utilisant les lois de Kirchhoff calculer les courants I1, I2 et I3.
2) Déterminer le générateur de Thévénin entre les bornes A et B.
3) Déduire le courant I3.
4) Calculer la ddp VC-VD entre les points C et D de trois manières (branche CE1D, CE2D et CE3D)
Figure 13
Exercice XI
On considère le circuit de la figure 14 ci-dessous.
1) Déterminer le courant instantané i(t).
2) Calculer la puissance active P consommée dans le circuit.
Figure 14
R1=100Ω, R2= 1000Ω, C=5µF, L=2mH et 
Exercice XII
Calculer les courants I1 et I2 de la figure 15 ci-dessous :
Figure 15

Page 5 sur 7
Exercice XIII
On considère le circuit suivant (figure 16) :
1) Déterminer le générateur de Thévénin vu entre les bornes A et B ;
2) Déduire le courant traversant la résistance
10
c
R
.
3) Calculer le courant dans la résistance Rc en transformant le générateur de tension (E, R1) en générateur de
courant.
Figure 16
Exercice XIV*.
Une installation (U=100V ; f=100Hz) alimente l’association parallèle d’un condensateur (c) parfait de capacité C=5µF
et d’une bobine idéale (L) d’inductance L=100mH (figure 17).
1)- Déterminer l’intensité I du courant et le déphasage φ entre courant I et la tension u.
2)- Déterminer les intensités I1 et I2 ainsi que leurs déphasages par rapport à la tension u.
3)- Calculer la puissance active P et réactive Q consommées dans le circuit.
Figure 17
Exercice XV :
Figure 18
E=20V ; R1=2k Ω ; R2=3k Ω ; R3=5k Ω; R6=4k Ω.
On considère le circuit ci-dessus (Figure 18).
1)- Déterminer le potentiel du point B qui sera par la suite pris comme potentiel de référence.
2)- On ouvre les interrupteurs K1 et K2. Calculer le potentiel du point A.
3)- Calculer la résistance vue des bornes A et B ( le circuit à droite du trait interrompu étant débranché).