Optique géométrique : Bases et principes

1. Nature de la lumière
1.1. La lumière comme onde ou corpuscule
Dans la théorie classique de l’électromagnétisme de MAXWELL , la lumière est une onde
1
électromagnétique, c’est-à-dire la propagation d’un champ électrique et d’un champ magnétique
perpendiculaires entre eux et à la direction de propagation :
Comme toutes les ondes, la lumière peut s'analyser en utilisant l'analyse spectrale!; on peut la
décomposer en ondes dites «!monochromatiques!» (signaux purement sinusoïdaux caractérisés par une
fréquence et une longueur d’onde spécifiques). On peut observer les composantes monochromatiques
de la lumière en faisant passer la lumière du jour dans un prisme ou lorsqu'un arc-en-ciel se produit.
Ce modèle permet d’interpréter efficacement les phénomènes de diffraction et d’interférences
de la lumière.
James Clerk MAXWELL (1831-1879) : physicien et mathématicien écossais majeur. Il a unifié les théories jusque là
1
séparées de l’électricité et du magnétisme. Il y inclut la lumière en s’appuyant sur les travaux de Michael Faraday. Ses
travaux font de lui le physicien ayant le plus influencé la physique du 20ème siècle (relativité restreinte et mécanique
quantique).
TSI 1 - Bases de l’optique géométrique
Page sur 1 7
Thème 1
Ondes et
Signaux
3
Bases de l’optique géométrique
La lumière dans le spectre électromagnétique
La lumière est ainsi une onde transverse qui se propage à la célérité c!=!3,00.108!m.s-1 dans le
vide.

Par contre, le modèle classique n’explique pas certaines manifestations comme les spectres de
raies des atomes ou l’effet photoélectrique. Il faut pour cela admettre l’existence de «!particules de
lumière!» qui traduisent l’aspect corpusculaire de la lumière. Ce double comportement est appelé dualité
onde-corpuscule de la lumière. Pour l’expliquer, il faut avoir recours à la mécanique quantique même si la
théorie corpusculaire de la lumière a eu des défenseurs antérieurs
En 1900, l'allemand Max PLANCK propose une explication du spectre d'émission des corps noirs
2
(corps qui absorbe toute l'énergie électromagnétique qu'il reçoit et qui la réémet sous forme de lumière si
sa température est suffisamment élevée). L'énergie émise est alors fonction de la température du corps
noir. Problème : la physique classique prévoyait des énergies émises infinies pour les faibles longueurs
d’onde ; c'est la «!catastrophe ultraviolette!». Pour réconcilier résultats d'expérience et théorie, Planck
postule que l'énergie électromagnétique échangée entre la matière et le rayonnement, au lieu d'être
continue comme en physique classique, ne peut prendre que des valeurs discrètes. Peu convaincu par son
hypothèse, il faut attendre 1905 qu’Albert EINSTEIN étaye cette théorie des quanta.
3
1.2. Sources de lumière
Un objet est visible s’il émet de la lumière : cette émission peut être intrinsèque et on parle alors
de source primaire ; ou l’objet peut diffuser la lumière émise par une autre source, l’objet est alors une
source secondaire. Parmi les sources primaires, on peut citer :
• les sources de lumière blanche : la principale est le Soleil. On trouve aussi les lampes à
incandescence dans lesquelles un filament de tungstène chauffé émet une onde
électromagnétique dont une partie importante se trouve dans le domaine visible (mais aussi
beaucoup dans l'infrarouge).
Max PLANCK (1858-1947) : physicien allemand, prix Nobel de physique en 1918 pour ses travaux sur la théorie des
2
quanta. Il est l’un des fondateurs de la mécanique quantique. De ses travaux fut conceptualisée l'ère de Planck, période
de l'histoire de l'Univers au cours de laquelle les quatre interactions fondamentales étaient unifiées.
Albert EINSTEIN (1879-1955) : physicien théoricien né allemand et mort helvéto-américain. Il est le père des théories
3
de la relativité restreinte et de la relativité générale. Il contribue largement au développement de la mécanique
quantique (prix Nobel 1921 pour l’explication de l’effet photoélectrique) et de la cosmologie. Il est l’un des plus grands
scientifiques de l’histoire dont il est impossible de résumer l’impact dans une note de bas de page…
TSI 1 - Bases de l’optique géométrique
Page sur 2 7
L'énergie ne peut être échangée que par petits "paquets", nommés quanta d’énergie. Le plus
petit quantum d’énergie pour un rayonnement de fréquence 𝝂 vaut
h est la constante de Planck : h = 6,62607015.10-34 J.s
La lumière est alors pensée comme constituée de «!petits grains!», baptisés PHOTONS en 1926
par le chimiste Lewis. Chaque photon transporte le quantum d’énergie E = h𝜈.
E=hν=h
c
λ
Spectre de la lumière solaire
intensité
λ
intensité
λ
Spectre d’une ampoule à incandescence

C'est l'agitation des particules chargées et chauffées qui est la cause du rayonnement. On parle
alors de rayonnement thermique. Le spectre d'émission est continu!: il contient toutes les longueurs
d'onde du visible mais celles-ci ne sont pas toutes émises avec la même intensité.
Même si elles sont économiques, le rendement trop faible des lampes à incandescence fait qu'on
leur préfère aujourd'hui les ampoules basse consommation. Leur fonctionnement repose sur le
phénomène de fluorescence, qu'on ne détaillera pas ici.
• les lampes spectrales : elles sont constituées d'une ampoule renfermant des vapeurs issues
d'atomes spécifiques. Les propriétés (en particulier la couleur) de la lumière émise dépendent
de l'élément chimique contenu dans l'ampoule. On parle ainsi de lampe à vapeur d'hydrogène,
de sodium (utilisées pour l'éclairage public) ou encore de mercure (cf TP).
En appliquant une forte tension à l'ampoule, on contraint les atomes à s'agiter fortement et à
entrer en collision les uns avec les autres. Ainsi, les atomes acquièrent temporairement des
énergies supérieures à leur énergie la plus basse (on parle dans ce cas d'état fondamental
d'énergie). Les atomes ne peuvent pas rester dans ces états de haute énergie (dits états excités)
et vont spontanément se débarrasser de ce surplus d'énergie en émettant un rayonnement de
fréquence (et donc de longueur d'onde) spécifique et quantifié (c'est-à-dire que la fréquence et
la longueur d'onde ne peuvent prendre que des valeurs bien déterminées).
Le spectre d'une lampe à vapeur atomique (observé à l'aide d'un prisme ou d'une
spectromètre) présente donc des raies fines et isolées les unes des autres. On parle de spectre
de raies.
• les lasers : ils peuvent être considéré comme une source de lumière monochromatique (c'est-
à-dire ne contenant qu'une seule longueur d'onde). C'est l'abréviation de Light Amplifier by
Stimulated Emission of Radiation (amplificateur de lumière par émission stimulée de
rayonnement).
TSI 1 - Bases de l’optique géométrique
Page sur 3 7
Dans le vide, on pourra retenir les correspondances suivantes entre couleur et longueur d’onde!:
λ (nm)
500
550
600
650
Couleur
Bleu
Vert
Jaune orangé
Rouge
Spectre d’un laser He-Ne

2. Propagation de la lumière dans un milieu transparent, homogène et isotrope
2.1. Indice optique et longueur d’onde
La lumière se propage dans le vide (à la célérité c = 299 792 458 m.s-1 ≈ 3,00.108 m.s-1) mais aussi
dans une grande variété de milieux transparents (qui n'absorbent pas l'énergie lumineuse), homogènes
(propriétés physiques du milieu identiques en tout point) et isotropes (propriétés physiques du milieu
indépendantes de la direction de propagation de la lumière) comme l'eau, l'air, le verre,…
Les milieux de propagation de la lumière ne se distinguent les uns des autres que par la vitesse v à
laquelle la lumière s'y propage.
On peut citer quelques valeurs :
Remarque : L'indice optique d'un milieu dépend de la fréquence de l'onde lumineuse. Ainsi, les
différentes composantes monochromatiques d'un signal lumineux ne se propagent pas toutes à la même
vitesse. C'est le phénomène de dispersion, qui est responsable de la décomposition de la lumière par un
prisme.
2.2. Approximation de l’optique géométrique
Lorsque l'on peut négliger le caractère ondulatoire de la lumière, on peut raisonner
géométriquement en considérant que la lumière se propage le long de rayons lumineux, courbes décrites
par la lumière pour aller d’un point à un autre.
Les rayons lumineux se propagent alors en ligne droite dans tout milieu transparent, homogène et
isotrope : on évite la diffraction, tous les systèmes étant suffisamment grands devant la longueur d’onde
de la lumière.
Les rayons lumineux n'interagissent pas entre eux (un rayon lumineux ne peut pas être dévié par un
autre) : il n'y a pas d’interférences possibles.
TSI 1 - Bases de l’optique géométrique
Page sur 4 7
On peut alors caractériser un milieu transparent par un nombre sans dimension appelé indice
optique du milieu : car la lumière se propage toujours moins vite dans un milieu transparent
que dans le vide.
n=
c
v> 1
Milieu
Indice optique
Vide
1 (exactement)
Air
1,0003 ≈ 1
Eau
1,33
Verre
1,35 à 1,8 (valeur typique : 1,5)
Diamant
2,4

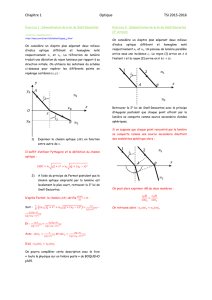
3. Réflexion et réfraction : lois de SNELL-DESCARTES
Dans l’approximation de l’optique géométrique, on peut se poser la question de ce qu'il advient
de la lumière lorsqu'elle change de milieu de propagation.
On appelle dioptre la surface de séparation entre deux milieux transparents d'indices différents n1
et n2. Si cette surface est plane, on parle de dioptre plan. Lorsqu’un rayon lumineux, dit incident, arrive
sur un dioptre, il donne en général naissance à un rayon réfléchi et à un rayon réfracté. A partir du point
d’intersection entre le rayon incident et le dioptre (point d’incidence), on définit la normale au point
d’incidence, droite perpendiculaire au dioptre. La normale au point d’incidence et le rayon incident
définissent le plan d’incidence.
3.1. Lois de Snell-Descartes pour la réflexion
4
Willebrord SNELL (1580-1626) : humaniste, mathématicien et physicien néerlandais. Il énonce les lois de la réfraction
4
vers 1625.
René DESCARTES (1596-1650) : mathématicien, physicien et philosophe français. Parmi ses nombreux travaux, il
établit les lois de la réfraction en 1637, indépendamment de Snell.
TSI 1 - Bases de l’optique géométrique
Page sur 5 7
Lois de Snell-Descartes pour la réflexion :
• le rayon réfléchi et le rayon incident appartiennent au plan d’incidence ;
• les angles d’incidence i et de réflexion r, orientés à partir de la normale au point d’incidence
sont tels que r = - i.
Rayon réfracté