1
CORRIGE – TD – Optique géométrique – SMIA – 2017/18
Série 2 – Miroirs & Dioptres
1.
Exercice 1 : Rétroviseur
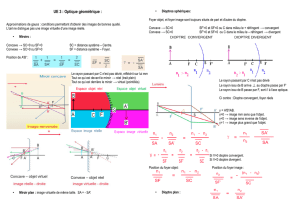
1) D’un objet éloigné, un miroir concave donne une image réelle renversée : ce n’est vraiment
pas souhaitable pour un rétroviseur… On considère donc un miroir convexe, qui donne ici
une image virtuelle et droite (figure 1).
La relation de conjugaison du miroir sphérique avec origine au sommet s’écrit :
avec un grandissement :
Ce qui donne : R = 10 m.
Le miroir du rétroviseur, convexe
, a un rayon de courbure de
10 m.
2) Pour le rayon limite réfléchi (figure 2), on
perçoit le bord du champ accessible :
(donc ) pour
D = 100 m.
Sachant que
, on obtient
. Et le rayon limite
indique:
Soit, r ≈ 12 cm , ce qui est une valeur raisonnable.
Discutons à présent l’approximation de Gauss : le rayon r est largement inférieur au rayon de
courbure R, donc le miroir est bien utilisé au voisinage de son sommet.
D’autre part :
est inférieur à 10°, donc les rayons sont peu inclinés.
Les conditions de Gauss sont donc satisfaites, d’ailleurs l’expérience montre que l’image ne
subit pas de distorsion notable.

2
Exercice 2 : Association de miroirs – Le télescope du Pic-du-Midi
SVP adoptez la notation au lieu de dans le corrigé …
Exercice 3 : Association de miroirs - Télescope du type Cassegrain
1. On utilise la méthode des images intermédiaires : l’image à travers le miroir primaire (M1 ),
d’un point O situé à l’infini sur l’axe optique des deux miroirs, est le foyer image F1 de celui-
ci, défini par
m
R
SF 513,5
21
11
. L’image O’ de F1 par le miroir secondaire (M2 ) est ensuite
donnée par la formule de conjugaison de ce miroir avec origine au sommet S2 :
Avec,
et
. On calcule alors
puis,
: l’image se forme pratiquement à 1,5 m derrière le miroir
primaire (M1 ).
2. L’image A’B’ à travers le télescope d’un objet AB situé à l’infini et centré sur l’axe optique est
située dans le plan de front contenant le point O’ déterminé à la question précédente
(propriété d’aplanétisme approché des miroirs sphériques dans les conditions de Gauss), c’est-
à-dire dans le plan perpendiculaire à l’axe optique et contenant O’.

3
Afin de caractériser cette image, on utilise là encore la méthode des images intermédiaires :
l’image intermédiaire de l’objet à travers le miroir primaire (M1 ) se forme dans le plan
focal de celui-ci et mesure
, où l’angle doit ici être exprimé en radian (voir
figure ci-dessous).
Donnez ici le grandissement avec origine au foyer (non vu dans le cours !) :
Le grandissement avec origine au foyer de l’image intermédiaire à travers le miroir
secondaire (M2 ) est donné donc par :
d’où,
Soit finalement, avec
,
et exprimé en radian :
.
La taille de l’image définitive :

4
Exercice 4 : La boule semi-argentée
SVP adoptez la notation
et
au lieu de et dans le corrigé …

5
Exercice 5 : Association de dioptres
Il s’agit de l’association d’un dioptre plan et d’un dioptre sphérique convexe dont l'indice
optique est n et son épaisseur HS.
1/ La face d'entrée de la lumière est la face plane.
dioptre dioptre
1
plan sphérique
A A A '
Pour le dioptre plan
1
n1
0
HA HA
(1)
Pour le dioptre sphérique
1
1 n 1 n
SA' SA SC
(2)
Foyer objet F ?
dioptre dioptre
1
plan sphérique
F A A'( )
SA'
1n
SA SC
n1
la relation (1)
11
1 n n n n(n 1)
n
HF HA HS SA (n 1)HS nSC
HS SC
n1
(n 1)HS nSC
HF n(n 1)
1 n 1
SF HS SC
n n 1
1 1,5 1
SF 1,5 ( 10)
n 1,5 1
SF 20,5cm
Foyer image F’ ?
dioptre dioptre
1
plan sphérique
A( ) A F'
HA
1
HA
1
SA
la relation (2)
1 1 n
SF' SC
SC
SF' 1n
R
SF' n1
SF' 20 cm
2/ Si
HS
est très petite, on retrouve une lentille mince.
SC
SF' SF 1n
SF' SF 20 cm
3/ Si la face d’entrée est la face sphérique, alors (en appliquant le principe du retour inverse de
la lumière) les rôles joués par les foyers calculés en 1/ s’inversent.
SF 20 cm
et
SF' 20,5 cm
 6
6
 7
7
1
/
7
100%