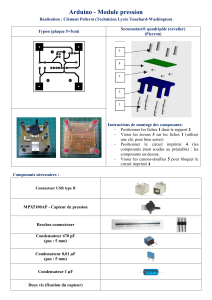
Resumé de cours : régimes transitoires électriques
S. Benlhajlahsen - PCSI1
88
87
86
85
84
83
82
81
80
79
78
77
76
75
74
73
72
71
70
69
68
67
66
65
64
63
62
61
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
I Circuit linéaire du second ordre
•Circuit (R,L,C)série
On considère le montage de la figure 1. On ferme l’interrupteur à t=0 et on suppose que le condensateur est
initialement déchargé.
KR L
C
EuC
i(t)
FIGURE 1 – Circuit (R,L,C) pour la charge du condensateur.
Capacité exigible : Analyser, sur des relevés expérimentaux, l’évolution de la forme des régimes transitoires en
fonction des paramètres caractéristiques.
0t
uC
E
FIGURE 2 – Régime pseusopério-
dique d’une charge de condensa-
teur.
0t
uC
E
FIGURE 3 – Régime apériodique
d’une charge de condensateur.
0t
uC
E
FIGURE 4 – Régime critique d’une
charge de condensateur.
Capacité exigible : Prévoir l’évolution du système à partir de considérations énergétiques.
Réponse :
— Un bilan de puissance pour la charge donne :
∀t>0, d
dt1
2Li2+1
2Cu2
C=E·i−R·i2
L’énergie électromagnétique dans le circuit sera tendanciellement augmentée par le générateur et sera dimi-
nuée par la résistance.
Page 1/2

— Un bilan de puissance pour la décharge donne :
∀t>0, d
dt1
2Li2+1
2Cu2
C=−R·i2⩽0
Autrement dit, la résistance va produire une diminution irrémédiable de des énergies électromagnétiques
stockées dans le condensateur et la bobine.
Capacité exigible : Écrire sous forme canonique l’équation différentielle afin d’identifier la pulsation propre et le
facteur de qualité.
Réponse : Dans le cas d’un régime transitoire d’ordre deux, l’équation différentielle peut se mettre sous la forme
canonique :
d2u
dt2+ω0
Q
du
dt+ω2
0u(t) = second membre (cours de physique)
d2u
dt2+2ξω0du
dt+ω2
0u(t) = second membre (cours de SII)
où :
—Qle facteur de qualité (facteur sans dimension);
—ω0est la pulsation propre : c’est la pulsation obtenue lorsqu’il n’y a pas d’amortissement a;
—ξ=1
2Qle facteur d’amortissement.
a. C’est donc la pulsation de l’oscillateur harmonique associé.
Capacité exigible : Décrire la nature de la réponse en fonction de la valeur du facteur de qualité.
Réponse : On distinguera :
— le régime pseudo-périodique obtenu pour Q>1
2: c’est un régime de faible amortissement où le « retour à
l’équilibre » se fait via une oscillation amortie;
— le régime apériodique obtenu pour Q<1
2: c’est un régime d’amortissement élévé;
— le régime critique qui est la situation où Q=1
2
Capacité exigible : Déterminer la réponse détaillée dans le cas d’un régime libre ou d’un système soumis à un
échelon en recherchant les racines du polynôme caractéristique.
Capacité exigible : Déterminer un ordre de grandeur de la durée du régime transitoire selon la valeur du facteur
de qualité.
Réponse : Le temps caractéristique du régime transitoire est τ=1
ξω0=2Q
ω0. En effet, ces différents régimes s’at-
ténue comme exp −t
τ=exp −ω0·t
2Q.
Page 2/2
1
/
2
100%