ChingMath-6eme-geometrie-plane-cercles

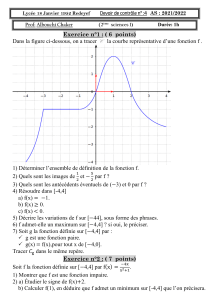
Sixième / Géométrie plane: cercles
1. Cercle
E.1
On considère le cercle Cdessiné
ci-contre de centre O.
Nommer chacun des segments
représentés sur la figure, les
nommer et donner leurs na-
tures.
O
A
B
C
D
E
C
E.2
On considère le cer-
cle Cde centre O
représenté ci-contre.
Recopier et compléter
les énoncés suivant
en utilisant les signes
∈et ̸∈ pour in-
diquer l’appartenance
ou non d’un point au
cercle :
C
A
B
C
D
E
F
G
HI
1A : : : C2B : : : C3C : : : C
4D : : : C5E : : : C6F : : : C
7G : : : C8O : : : C
E.3 Sur la figure ci-dessous sont représentés :
six cercles C1,C2,C3,C4,C5et C6;
six points A,B,C,D,Eet Fdu plan.
E
C1
A
C2
F
C3
CC4
B
C5
D
C6
Associer chaque cercle à son centre.
E.4 On considère les deux cercles Cet C′
de centres respectifs Iet Jet de même diamètre.
Les points A,I,B,Jet Csont alignés.
ABC
I J
C C ′
1 Justifier que le segment [AB]est un diamètre du cercle
C.
2 Parmi, les phrases suivantes, lesquelles sont correctes?
Cest le cercle de centre I.
Cest un cercle de centre I.
C′est le cercle de centre Jet de diamètre [AB].
C′est le cercle de centre Jet de diamètre AB.
E.5 On considère la figure ci-dessous qui est
composé du cercle Cde centre Bet de diamètre [AC]et du
cercle C′de centre Aet de rayon [AD]. Le cercle C′passe
par le point B.
A
B
C
C
C′
D
1 Citer tous les segments de longueurs égales dans cette
figure en justifiant vos affirmations.
2 Comparer, en justifiant les longueurs suivantes :
aAC et AB+BC bDA+AC et DC
Indication : pour comparer ces longueurs, on pourra utiliser
le compas pour reporter des longueurs sur la droite ci-
dessous :
https://chingmath.fr

E.6 On considère les 26 points ci-dessous :
BC
D
E
F
G
H
I
J
KL
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
A
Citer l’ensemble des points ayant une distance de trois cen-
timètres du point A.
E.7 Expliquer en quelques mots, en quelques
phrases :
1 La différence entre le rayon et le diamètre du cercle.
2 La différence entre le cercle et le disque.
E.8
La spirale de Fibonacci permet de construire une spirale par
des quarts de cercle construit à partir de carré réduit les uns
des autres grâce au nombre d’or.
Dans la figure ci-dessous, est représenté une partie de la spi-
rale de Fibonacci avec quatre quarts de cercle.
AB
C
D
EF
G
H
IJ
KL
Décrire chacun de ces quarts de cercle.
E.9
“Le Ying et le Yang” est un concept du Taoïsme qui
représente deux forces opposées mais complémentaire.
Cette figure est composée d’un cercle et de deux demi-
cercles.
A B
O
Pour construire cette figure (à droite), on utilise le cercle de
centre Otel que les points Aet Bappartiennent à Cet tel
que les points O,A,Bsont alignés.
Décrire les cercles et demi-cercles composant cette figure.
E.10 Dans le plan, on considère les 6points
ci-dessous :
A
BC
D
E
F
1 Tracer le cercle C1ayant pour centre Aet pour rayon le
segment [AB].
2 Tracer le cercle C2ayant pour diamètre [CD].
3 Tracer le cercle C3admettant le segment [EF ]pour
corde.
2. Cercle et égalité de longueurs
E.11 On considère la figure ci-dessous où :
Le point Iest le milieu du segment [AB];
Le cercle C1a pour centre le point Bet passe par A;
Le cercle C2a pour centre Iet passe par le point A.
Le point Mappartient au cercle C1et il est tel que le
cercle C3de centre Mpasse par les points Aet B.
A
B
C1
IC2
M
C3
https://chingmath.fr

1 Pour chacun des cercles C1,C2et C3, préciser la nature
du segment [AB].
2 Placer le point Cdiamétralement opposé au point Adans
le cercle C1.
3 Quelle particularité possède le triangle ABM? Justifier
votre réponse.
E.12 On considère la figure ci-dessous où :
AB =BC =CD =DE = 2 cm
C1,C2,C3sont des demi-cercles de diamètres respectifs
[AC],[BD],[CE].
A B C D E
M N
C1
C2C3
1 a Justifier que BC =BM.
b Justifier que CB =CM =CN =CD.
c Justifier que DC =DN.
2 a Quelles sont les natures des triangles BCM et
CDN ?
b On nomme Ile milieu du segment [BC]et Jle milieu
du segment [CD]. Quelle est la nature du quadrilatère
MNJI?
c Justifier que le quadrilatère BCN M est un losange.
E.13 Effectuer le programme de tracer suivant:
1 Placer un point Osur cette droite (d)et tracer le cercle
Cde centre Oet de diamètre 4cm.
2 Le cercle Cintercepte la droite (d)aux points Aet B.
3 Tracer le cercle C′de centre A. Il intercepte la droite (d)
en un nouveau point nommé M.
4 Tracer le cercle C′de centre B. Il intercepte la droite
(d)en un nouveau point nommé N.
E.14 Dans le plan ci-dessous, on considère les
huit points représentés ci-dessous :
A
B
C
D
E
H
G
F
Sans utiliser, ni le compas, ni la règle graduée, répondre aux
questions suivantes :
1 On considère le cercle Cde centre Aet passant par le
point B.
a Justifier que le point Cappartient au cercle C.
b Justifier que le point Dn’appartient pas au cercle C.
2 On considère le cercle C′de centre Eet passant par le
point B.
Compléter les pointillés ci-dessous avec les symboles ∈et
̸∈. Justifier vos affirmations.
B : : : C′;F : : : C′;G : : : C′;H : : : C′
Question subsidiaire : les points B,D,Happartiennent
à un même cercle. Déterminer le centre de ce cercle.
3. Programme de contruction
E.15
1 Réaliser le programme de constructions ci-dessous :
Tracer un segment [AB]tel que AB =5 cm
Tracer le cercle Cde centre Aet passant par le point
B.
Tracer le cercle C′de centre Bet de diamètre 10 cm.
Nommer Met Nles deux points d’intersection des cer-
cles Cet C′.
Tracer la droite (d)passant par les points Met N.
Nommer Ple point d’intersection de la droite (d)et du
segment [AB].
2 a Que peut-on dire de la position relative des droites
(AB)et (d)?
b Que peut-on dire de la position du point Psur le seg-
ment [AB]?
4. Rédiger un programme de construction
https://chingmath.fr

E.16 On considère la configuration ci-
dessous :
DB
E
F
C
A
(AC)==(BE)
(EF )==(BD)
C
(∆′)(∆) (d)
Écrire le programme de construction en commençant par :
“Tracer un triangle BED.”
5. Autour de la tangente
E.17 Un skieur s’apprète à sauter sur une bosse
pour atterir de l’autre côté de la piste. On suppose qu’en
plein vol, la trajectoire du skieur sera un arc de cercle.
O
Saut 1
1 On admet que le cercle qui représente le mieux la trajec-
toire du skieur et lui permette d’avoir la meilleur “récep-
tion” à l’atterissage a pour centre O.
Tracer cette trajectoire du skieur.
Indication : dans des conditions idéales, la trajectoire du
skieur sera une parabole. Cette courbe bien différente du
cercle sera étudiée au lycée.
Si contre, une trajectoire en parabole possible du skieur.
Saut 2
Toujours en supposant que la trajectoire du skieur est un arc
de cercle, on souhaite connaitre sa trajectoire lors du “saut 2”
afin que sa réception soit “idéale” mais cette fois, il va falloir
déterminer le centre du cercle de sa trajectoire.
Pour cela, commençons à analyser la trajectoire du “saut 1”.
2 Sur la figure du “saut 1”, prolonger la di-
rection rectiligne du skieur lors de sa prise
d’appui et remarquer toutes les propriétés
entre cette droite, le cercle et le point
d’impulsion du skieur.
O
Saut 1
3 Reproduire toutes les propriétés de la question 2 afin
de déterminer la position exacte du centre de ce cercle.
Puis, tracer la trajectoire du skieur lors du “saut 2”.
E.18
6. Autour de la tangente (version 2)
E.19
https://chingmath.fr

Ci-contre, un sangaku, un dessin
japonais traditionnel.
Reproduire ce dessin dans la
figure ci-dessous où le triangle
équilatéral et les centres des cer-
cles ont été donnés.
Indication : la précision des points de contacts des dif-
férents objets d’un Sangaku est primordial.
E.20 L’exercice n’existe pas.
https://chingmath.fr