1/3
ighirane@elaraki.ac.ma
Elaraki International School of Morocco
Exercice 1 : Pile cuivre – Argent ( 8 points )
Soit la pile mettant en jeu les couples
et
l'équation globale de la
réaction s’écrit :
L’une des deux demi-piles est réalisée à partir de 250 mL d’une solution de sulfate de cuivre
telle que
= 0,2 dans laquelle on plonge une lame de cuivre de masse 45 g.
L’autre demi-pile est réalisée à partir de 250 mL d’une solution de nitrate d’argent telle que
= 0,3 dans laquelle on plonge une lame d’argent de masse 20 g .
Cette pile débite, à travers un conducteur ohmique, un courant d’intensité constante .
1) En exploitant le critère d'évolution d'un système chimique déterminer le sens d'évolution de
la réaction , en justifiant votre réponse.
2) Indiquer la polarité de chaque électrode et le sens conventionnel du courant à l’extérieur de la
pile.(Justifier votre réponse).
3-1) indiquer le sens de déplacement des différents porteurs de charge dans les différents parties
de la pile (préciser la nature du porteur de charge , le milieu et le sens de déplacement)
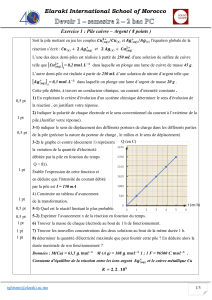
3-2) le graphe ci-contre (document 1) représente
la variation de la quantité d'électricité
débitée par la pile en fonction du temps
Q = f(t).
Établir l'expression de cette fonction et
en déduire que l'intensité du courant débité
par la pile est I = 150 mA
4) Construire un tableau d’avancement
de la transformation.
5-1) Quel est le réactif limitant le plus probable.
5-2) Exprimer l’avancement x de la réaction en fonction du temps.
6) Trouver la masse de chaque électrode au bout de 1 h de fonctionnement.
7) Trouver les nouvelles concentrations des deux solutions au bout de la même durée 1 h.
8) déterminer la quantité d'électricité maximale que peut fournir cette pile ? En déduire alors la
durée maximale de son fonctionnement ?
Données : M(Cu) = 63,5 M (A g) = 108 1 ; 1 F = 96500 C .
Constante d'équilibre de la réaction entre les ions argent
et le cuivre métallique Cu
0
540
1080
1620
2160
2700
3240
0 1 2 3 4 5 6
Q (en C)
t (en h)
0,5 pt
1 pt
0,5 pt
1 pt
1 pt
0,5 pt
0,5 pt
1 pt
1 pt
1 pt

2/3
ighirane@elaraki.ac.ma
Elaraki International School of Morocco
Électricité 12 points
Première partie: Charge et décharge d'un condensateur dans une bobine.
Pour cela, on réalise le circuit électrique schématisé sur la qui comporte :
- un générateur de tension de f.e.m. E ;
- deux conducteurs ohmiques de résistance r = 20Ω et R.
- une bobine (b) d’inductance L et de résistance .
- un condensateur de capacité C initialement déchargé.
- un interrupteur K à double position.
1- Etude du dipôle RC lors de la charge du condensateur :
A un instant de date t = 0, on place l’interrupteur K en
position (1) . Un système d’acquisition informatisé permet de tracer la courbe d’évolution de la
tension . La droite (T) représente la tangente à la courbe à la date t = 0.
1.1. Etablir l’équation différentielle vérifiée par
1.2. Trouver les expressions de A et de , pour que
soit solution de cette équation
différentielle.
1.3. L’intensité du courant électrique s’écrit sous forme :
Trouver l’expression de I0 en fonction de
E, r et R.
1.4. En exploitant la courbe de la figure 2 :
1.4.1. Trouver la valeur de la résistance R sachant que
1.4.2. Déterminer la valeur de .
1.4.3. Vérifier que la capacité du condensateur est C =10µF.
2-Etude de l’amortissement et de l’entretien des oscillations dans un circuit RLC
Une fois le condensateur est totalement chargé, on bascule l’interrupteur K vers la position (2) à
un instant que l’on choisira comme
nouvelle origine des dates (t = 0) .
La courbe de la figure 3, représente
l’évolution temporelle de la charge q(t) du
condensateur.
2.1. Identifier le régime oscillatoire qui
correspond à la courbe de la figure 3.
2.2. En assimilant la pseudo période à la
période propre de l’oscillateur électrique,
déterminer l’inductance L de la bobine (b) .
2.3. Calculer ΔE , la variation de l’énergie
totale du circuit entre les instants t1 = 0ms
et t2 =18ms , puis interpréter ce résultat.
2.4. Pour entretenir les oscillations, on
monte en série avec le condensateur et la
bobine (b), précédemment étudiés, un
figure1
1 pt
1 pt
1 pt
0,5 pt
0,5 pt
0,5 pt
0,5 pt
1 pt
1 pt

3/3
ighirane@elaraki.ac.ma
Elaraki International School of Morocco
générateur (G) qui délivre une tension proportionnelle à l’intensité du courant
électrique: .
2.4.1. Etablir l’équation différentielle vérifiée par la charge q(t) .
2.4.2. On obtient des oscillations électriques sinusoïdales lorsque la constante k prend la valeur
k =11 dans le système d’unités internationales.
En déduire la valeur de la résistance électrique de la bobine (b).
Deuxième partie: Etude de la modulation d’amplitude
Le but de cette partie de l’exercice est l’étude de la modulation d’amplitude.
Au cours d’une séance de travaux pratiques, un
groupe d’élèves applique à l’entrée E1 du circuit
multiplieur une tension sinusoïdale d’expression
et à l’entrée E2 du
circuit multiplieur une tension sinusoïdale
d’expression correspondante
à une onde porteuse.
(U0 est la composante continue de tension)
2-1- L’expression de la tension à la sortie du
circuit multiplieur est :
avec k une constante caractérisant le circuit
multiplieur.
Montrer que l’amplitude de la tension s’écrit
sous la forme :
en précisant les expressions de A et m.
2-2- Après réglage des sensibilités de
l’oscilloscope sur : 1V/div et 0,5 ms/div, les élèves
ont visualisé la tension de sortie :
obtenue. La
figure 5 représente les variations de cette tension.
Déterminer la fréquence f du signal
modulant, et la fréquence F de l’onde porteuse.
2-3- Montrer, en calculant la valeur du taux de modulation m, que la modulation est bonne.
La transmission d’informations sur de grandes distances à l’aides d’ondes électromagnétiques,
nécessite la modulation d’amplitude. Parmi les composants adoptés dans cette opération : le
circuit multiplieur.
1 pt
1 pt
1 pt
1 pt
1 pt
1
/
3
100%