Ecole Supérieure de Technologie et d’Informatique (ESTI) A.U : 2013/2014
Electronique de puissance : Chapitre 3 : Les hacheurs 2ING-MEC
Mr L.BOUSLIMI
Page 1
TD : Les Hacheurs
Exercice 4 :
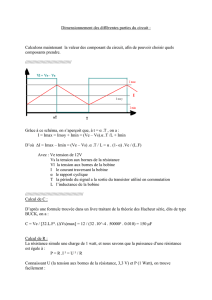
Le support de cet exercice est une porte automatique de garage collectif dans un immeuble. Le synoptique
concernant la partie électrique et une vue d’ensemble du dispositif sont donnés.
On s’intéresse plus particulièrement au hacheur série pilotant le moteur.
Etude du hacheur série :
La tension d’alimentation du hacheur série est constant et vaut Vs=210V.
D est une diode idéale sans seuil. K est un interrupteur parfait commandé
par une tension.
On note α le rapport cyclique de commande de ce hacheur et T la période
de fonctionnement.
- Pour t
∈
[0 ; αT], K est fermé
- Pour t
∈
[αT ; T], K est ouvert
On donne T=0,1ms.
On considère que la tension aux bornes du moteur est égale à sa fém.
E proportionnelle à la vitesse de rotation du moteur : E=kN avec k=5,25.10
-2
V(tr.min
-1
).
On suppose que l’intensité i du courant ne s’annule jamais et varie linéairement entre les valeurs minimale et
maximale I
min
et I
max
.
1) Déterminer l'expression de i(t) pour t
∈
[ 0 ; αT ] puis pour t
∈
[ αT ; T ].
2) Représenter les allures de v
D
(t) et i(t) sur une durée de 2T.
3) Exprimer la valeur moyenne de la tension v
D
(t) en fonction de α et Vs. En déduire la relation entre E, α et Vs.
4) Exprimer l’ondulation de courant ∆i=I
max
– I
min
en fonction de α, Vs, L et T.
5) Représenter l'allure de ∆i en fonction de α.
6) Pour quelle valeur de α l'ondulation de courant est-elle maximale ? Calculer (∆i)
max
.
7) Déterminer la valeur de αqui permet de régler la vitesse de rotation à N = 1000 tr.min
-1
.
8) Représenter les allures de i
D
(t) et i
k
(t)
et exprimer leurs valeurs moyennes respectives en fonction de α, I
min
et
I
max
.
Correction :
V
s
= 210 V. D est une diode idéale. K est un interrupteur parfait αest le rapport cyclique de commande de ce
hacheur et T = 0,1 ms la période de fonctionnement.
• Pour t
∈
[ 0 ; αT ], K est fermé
• Pour t
∈
[αT ; T ], K est ouvert.
La tension aux bornes du moteur est égale à sa fém. E proportionnelle à la vitesse de rotation du moteur :
E = k.N avec k = 5,25.10
-2
V/(tr.min
-1
).
L'intensité i du courant ne s'annule jamais et varie entre les valeurs minimale et maximale I
min
et I
Max
.
1) Expression de i(t) :
Pour t
∈
[ 0 ; αT ] :
V
s
= L
di/dt
+ E donc
di/dt
= (
V
s
–
E)/L
et i(t) = I
min
+ (
V
s
–E)
t
/L
Pour t
∈
[ αT ; T ] :
0 = L
di/dt
+ E donc
di/dt
=
− E/L
et i(t) = I
Max
+ [
−E/L
(t – αT)]

Ecole Supérieure de Technologie et d’Informatique (ESTI) A.U : 2013/2014
Electronique de puissance : Chapitre 3 : Les hacheurs 2ING-MEC
Mr L.BOUSLIMI
Page 2
2) v
D
(t) et i(t) sur une durée de 2T.
3) <v
D
>=
αV
s
E=αVs
4) Ondulation de courant ∆i = I
Max
- I
min
en fonction de α, V
s
, L et T.
5) Allure de ∆i en fonction de α
6) L'ondulation de courant est maximale pour α = 0,5.
(∆i)
max
=
V
s
T/4L=
52,5 mA.
7) Pour N = 1000 tr.min
-1
:
E = αVs = k N donc α =
kN
/
V
s AN : α= 0,25
8) Représenter les allures de i
D
(t) et i
k
(t).
<i
D
>= Aire du trapèze de base (1-
α)T
<i
k
>= Aire du trapèze de base
αT
1
/
2
100%