Fonction Comptage : Cours d'Automatismes GIM 1

O. IKHOUANE – Cours d’Automatismes – GIM 1
CHAPITRE 5
LA FONCTION COMPTAGE
La plupart des équipements numériques utilisent des compteurs. Un compteur est un
ensemble de bascules interconnectées par des portes logiques qui sert à compter les impulsions
arrivant sur son entrée Horloge. Le comptage peut s’effectuer dans différents codes : binaire pur,
BCD, Gray, etc. Hormis cette fonction principale, le compteur peut aussi être utilisé pour la division
de fréquence, les opérations de séquencement et les opérations arithmétiques.
1–INTRODUCTION
1.1 – Définitions
Définition 1 : un compteur est un circuit séquentiel comportant n bascules décrivant au rythme
d'une horloge un cycle de comptage régulier ou quelconque d'un maximum de 2n combinaisons.
Par exemple si le compteur contient 3 bascules, on pourra compter de 0 à
.
Définition 2 : la combinaison de sortie d'un compteur est appelé état du compteur.
Pour un compteur à 3 bascules, la séquence des états est la suivante : 000, 001, 010, 011,
100, 101, 110, 111.
Définition 3 : le nombre d'états possibles d'un compteur est appelé modulo. On dit encore que
c’est la capacité du compteur.
Un compteur modulo Npasse successivement par Nétats. Un compteur binaire naturel
compte de 0 à N – 1. Le graphe suivant présente les différents états parcourus par un
compteur modulo 8.
000
001
010
011
100
101
110
111
Figure 5.1 – Séquence de comptage modulo 8

2
1.2 – Classification des compteurs
Les compteurs peuvent être classés en fonction de 3 caractéristiques :
le type de basculement du compteur,
le sens du comptage,
le mode de comptage.
1.2.1 – Classification selon le type de basculement
Elle permet de différencier les compteurs asynchrones des compteurs synchrones.
a) Compteur synchrone
Dans un compteur synchrone, toutes les entrées d’horloges des bascules sont reliées à la
même entrée d’horloge et commutent en même temps.
b) Compteur asynchrone
Dans un compteur asynchrone, les bascules n’ont pas la même entrée horloge et
commutent indépendamment l’une de l’autre.
1.2.2 - – Classification selon le sens de comptage
Elle permet de différencier :
les compteurs (évolution croissante de l’état dans le temps),
les décompteurs (évolution décroissante de l’état dans le temps).
Certains d’entre eux peuvent assurer les deux fonctions : on les appelle compteurs
réversibles.
1.2.3 – Classification selon le mode de comptage
Elle permet de différencier :
les compteurs à cycle complet,
les compteurs à cycle incomplet.
Exemples :
Un compteur 4 bits qui compte de 0 à 15 en binaire naturel est un compteur à cycle
complet, car sa valeur de sortie utilise toutes les combinaisons possibles de ses
sorties.
Un compteur 4 bits qui compte de 0 à 9 seulement (on l’appelle aussi compteur BCD)
est un compteur à cycle incomplet, car les 16 combinaisons de ses 4 sorties ne sont
pas toutes utilisées.
Un compteur 6 bits qui décompte de 53 à 12 est un décompteur à cycle incomplet.
2–COMPTEURS ASYNCHRONES
2.1 – Compteur modulo 2
C’est le compteur le plus simple puisqu’il ne fait qu’un bit, mais il sera à la base de la
réalisation de tous les autres. On peut le réaliser avec une bascule JK ou une bascule D Edge

3
Triggered (uniquement, pas de D-latch) selon le schéma suivant. Les deux bascules sont montées
en diviseur par 2 :
les entrées J et K sont câblées à l’état 1, donc la bascule change d’état sur chaque
front efficace d’horloge,
l’entrée D reçoit , donc prend en compte l’état complémenté de la sortie Q sur
chaque front efficace d’horloge.
D
T
Q
Q
J
K
CK
Q
Q
H
5V
CK
Figure 5.2 – Compteurs modulo 2
Chronogramme
CK
Q0
1
0
1
0
1
Figure 5.3 – Chronogramme de fonctionnement d’un compteur modulo 2
Sur le chronogramme, on constate que la fréquence du signal sortant de Q est la moitié de
la fréquence du signal d’horloge. On dit que la bascule fonctionne en diviseur par 2.
2.2 – Compteur asynchrone modulo 2n
Un compteur asynchrone est constitué de n bascules J-K ou D fonctionnant en diviseur
par 2. Le signal d'horloge n'est reçu que par le premier étage (bascule LSB : Least Significant
Bit). Pour chacune des autres bascules, le signal d'horloge est fourni par une sortie de la
bascule de rang immédiatement inférieur.
Le comptage s’effectue en binaire pur et on pourra compter de 0 à 2n– 1 :
si n = 2, on compte de 0 à 3,
si n = 3, on compte de 0 à 7,
si n= 4, on compte de 0 à 15, etc.
2.2.1 – Application : comptage modulo 8
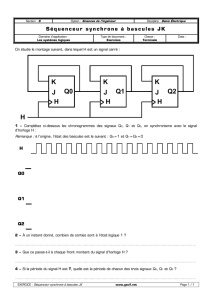
On a besoin pour cela de 3 bascules JK ou D. Le montage avec bascules JK est donné ci-
dessous.

4
J
K
CK
Q
Q
H
J
K
Q
Q
H
J
K
Q
Q
H
5V
012
Figure 5.4 – Compteur asynchrone modulo 8 avec bascules JK
Supposons les trois bascules à zéro à l'instant t = 0. Nous avons vu que pour une bascule
JK la sortie change d'état au moment du front efficace de l’horloge (ici front descendant).
L'évolution temporelle des trois sorties Q0, Q1 et Q2 est représentée sur le chronogramme ci-
dessous. La sortie Q0 bascule sur chaque front descendant du signal d'horloge. La sortie Q1
change d'état à chaque transition 1 → 0 de la sortie Q0. De même le basculement de la sortie Q2
est déclenché par une transition 1 → 0 de la sortie Q1.
CK
Q0
Q1
Q2
000 001 010 011 100 000101 001110 010111
Figure 5.5 – Chronogramme de fonctionnement d’un compteur modulo 8
A partir de ce chronogramme nous pouvons écrire la liste des états successifs des trois
sorties, donc la table de comptage.
CK
Q2
Q1
Q0
Décimal
0
0
0
0
0
0
1
1
0
1
0
2
0
1
1
3
1
0
0
4
1
0
1
5
1
1
0
6
1
1
1
7
Figure 5.6 – Table de comptage modulo 8
Nous avons réalisé un compteur s'incrémentant d'une unité à chaque impulsion d'horloge,
avec un cycle de huit valeurs de 0 à 7 (modulo 8). Nous constatons également que les sorties Q0,

5
Q1 et Q2 fournissent des signaux périodiques de fréquences respectivement 2, 4 et 8 fois plus
faibles. La division de fréquence est une des applications des compteurs.
2.2.2 – Compteur à cycle incomplet
On peut souhaiter compter jusqu'à un nombre N qui ne soit pas une puissance de 2, par
exemple 7 ou 12 dans le système décimal. Pour cela on va utiliser un compteur de n bascules, tel
que
. Ensuite, comme le cycle n’est pas une puissance de 2, la seule solution est d’agir sur
l’entrée « Clear » de chaque bascule lorsque la combinaison correspondant au modulo du
compteur se produit sur les sorties de celui-ci.
Exemple : compteur modulo 10
Nous voulons que l'entrée Clear soit à 0 lorsque le compteur atteint (10)10 = (1010)2. Pour
cela nous pouvons écrire l'expression logique :
0123 Q.Q.Q.QCl 
En fait, dans ce cas particulier, nous pouvons simplifier cette relation logique en ne tenant
compte que des sorties à 1 dans l'expression binaire de N. En effet il ne peut y avoir ambiguïté :
toute combinaison contenant les mêmes sorties à 1 et au moins une autre à 1 correspond à un
nombre plus grand que N et ne peut être rencontrée dans la séquence décrite par le compteur.
Pour un compteur modulo 10 nous pouvons donc utiliser
13 Q.QCl 
,ce qui nous conduit au
schéma ci-dessous (réalisation avec des bascules D.
D
T
Q
Q
CK
D
T
Q
Q
D
T
Q
Q
D
T
Q
Q
Q
3
Q
2
Q
1
Q
0
&
Cl Cl Cl Cl
Figure 5.7 – Compteur asynchrone modulo 10
Dès que la sortie de la porte NAND passe à 0, les bascules sont forcées à 0 : le compteur
se remet à compter à partir de 0.
CK
Q3
Q2
Q1
Q0
Décimal
0
0
0
0
0
0
0
0
1
1
0
0
1
0
2
0
0
1
1
3
0
1
0
0
4
0
1
0
1
5
0
1
1
0
6
0
1
1
1
7
1
0
0
0
8
1
0
0
1
9
1
0
1
0
10
Figure 5.8 – Table de vérité du compteur asynchrone modulo 10