chapitre Lentilles minces

Chapitre 4 : Les lentilles
1
1. Définition :
Une lentille est un milieu transparent homogène d’indice n limité par deux dioptres dont l'un au moins
est sphérique, l'autre pouvant être, à la limite, plan. C’est un système centré dont l’axe est la droite qui
joint les deux centres des dioptres respectifs.
L’épaisseur d’une lentille est la distance S1S2 où S1 et S2 sont les sommets des deux dioptres. Une
lentille est dite mince ou épaisse selon que son épaisseur est ou n’est pas petite devant les rayons de
courbure de ses deux faces et devant leur différence si ceux-ci sont de même sens.
2. Formes d’une lentille : Il existe six formes possibles de lentilles :
- lentilles biconvexes, - lentilles biconcaves, - lentilles plan-convexe, - lentilles plan-concaves
- ménisques à bords minces et ménisques à bords épais (cf. fig 1).
3. Nature d’une lentille : nous avons deux sortes de lentilles minces :
- les lentilles convergentes : ou lentilles à bords minces, où F est dans le milieu objet, F′ est alors dans
le milieu image.
- les lentilles divergentes : ou lentilles à bords épais, dont les deux foyers sont inversés. i.e. F est dans
le milieu image, F′ est alors dans le milieu objet.
Dans l’approximation, on représente les lentilles minces comme suite :
Lentille biconvexe
Lentille biconcave
Lentille plan-convexe
Lentille plan-concave
Ménisques à bords minces
Ménisques à bords épais
S1
S2
S1
S2
S1
S2
S1
S2
S1
S2
S1
S2
Fig1 : les déférentes formes de lentilles
O
F′
F
+
Espace objet
Espace image
Lentille convergente
O
F
F′
+
Espace objet
Espace image
Lentille divergente
Fig2 : représentation de lentilles minces

Chapitre 4 : Les lentilles
2
4. Relation de conjugaison et grandissement :
Pour une lentille mince d’indice de réfraction n (plongée dans l’air d’indice n0=1), de centre O et
de foyers objet F et image F’, la position de l’image d’un objet se détermine suivant la relation
suivante (relation de conjugaison):
Dans le cas d’une lentille les foyers F et F′ sont symétriques par rapport au centre O.
Quant au grandissement il est selon la relation suivante :
5. Foyers principal et secondaires :
Nous savons que caque faisceau parallèle se rencontre en un seul point :
- Foyer principal F et/ou F’ pour le faisceau parallèle à l’axe optique.
- Foyer secondaire pour les faisceaux. Ce foyer secondaire est un point qui appartient au plan
focal objet (FS) et/ou image(F’S). Le plan focal est le plan perpendiculaire à l’axe optique et qui
passe par le foyer principal F et/ou F’ (nous avons une infinité de foyers secondaires)
Pour trouver la direction de sortie pour un faisceau parallèle incident et/ou la direction des rayons
incidents pour un faisceau qui ressort parallèle, il suffit de représenter le plan focal objet et/ou image,
puis trace le rayon qui passe par le centre et qui est parallèle au faisceau, son intersection avec le plan
focal objet et/ou image sera également le point d’intersection du reste du faisceau parallèle..
O
F′
F
+
Foyer principal
image
O
+
F′
F
Foyer principal
objet
O
F′
F
+
Plan focal
image
F′S
O
F
F
’
+
Plan focal
objet
FS
Cas d’un foyer secondaire image
Cas d’un foyer secondaire objet

Chapitre 4 : Les lentilles
3
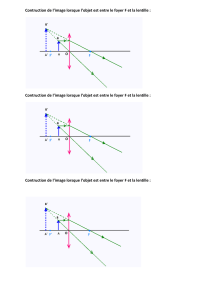
6. Construction géométrique :
On procède de la même manière que pour les dioptres sphérique, donc pour trouver graphiquement
l’image A’B’ d’un objet AB, il suffit de trouver le conjugué B’ de B en utilisant deux des trois rayons
principaux à savoir :
- Le rayon qui passe par le centre O ne sera pas dévié.
- Un rayon parallèle à l’axe optique sort en passant par le foyer image F’.
- Un rayon qui passe par le foyer objet F ressort parallèlement à l’axe optique.
Les différents cas possibles vont être vus dans l’exercice 2.
7. Association de lentilles :
On considère deux lentilles L1 et L2 de centres optiques O1 et O2, de distances focales
et dont les axes optiques sont confondus. Leur association réalise un
système appelé “doublet ”.
a- Doublet accolé :
Dans ce cas, les centres optiques O1 et O2 des deux lentilles L1 (de distance focale f’1) et L2 (de distance
focale f’2) sont confondus en O. ce système est équivalent à une lentille de centre O et de distance
focale f’ tel que :
b- Doublet non accolé :
Cette fois-ci, les centres optiques O1 et O2 des deux lentilles L1 (de distance focale f’1) et L2 (de
distance focale f’2) ne sont pas confondus et que 
Le doublet est toujours équivalent à une lentille unique L de distance focale équivalente f ' telle que :
B
F
O
F′
A
+
Espace objet
Espace image
a- Lentille convergente
B′
A′
O
F
F′
+
Espace objet
Espace image
b- Lentille divergente
Fig3 : construction géométrique dans une lentille
F1
O1
L1 +L2
O2
F’1
F2
F’2
↔
L
O
F
F’
Fig4 : doublet accolé
F1
O1
O2
F’1
F2
F’2
d
e
F’
F
L1
L2
Fig4 : doublet non accolé

Chapitre 4 : Les lentilles
4
De la figure 5, On constate que :
- Tout rayon incident qui émerge (sort) du système (doublet) parallèlement à l'axe, passe par le
foyer objet F de la lentille équivalente L. Or ce rayon passe par le foyer objet F2 de la lentille L2. Le
foyer F2 est donc l'image de F à travers la lentille L1.
- Tout rayon incident parallèle à l'axe émergera du doublet en passant par un point qui représente
donc le foyer image F' de la lentille équivalente L. Or ce rayon passe par le foyer image F'1 de L1. F'
est donc l'image de F'1 à travers la lentille L2.
- Tout rayon incident passant par F1 émerge du doublet en passant par F'2. F'2 est donc l'image de
F1 à travers le système (doublet) ou par la lentille équivalente L.
Le doublet est toujours équivalent à une lentille unique L de distance focale équivalente f ' telle que :
Ce système est celui utilisé dans la réalisation d’un microscope, qui permet d’observer des objets
microscopiques.
c- Doublet afocal :
Dans un tel doublet les foyers F'1 et F2 sont confondus (d = 0). D’où, tout rayon incident parallèle à l'axe
émerge (sort) du doublet parallèlement à l'axe (cf. fig.6).
Un tel système est utilisé pour l'observation d'objets éloignés, donc il est utilisé dans la réalisation d’une lunette
astronomique
F1
O1
O2
F’1 ≡F2
F’2
e
Fig6 : doublet afocal

Corrigé de la série N°3
5
Exercice N°1 :
1. Propriétés de la lentille :
- Elle doit être mince, i.e. la distance entre
les sommets des deux dioptres est négligeable
Et peut être assimilé à un point O.
- Les foyers F et F’ sont symétriques par rapport à O.
2. Relation de conjugaison :
Nous avons :   
En I : la lumière passe d’un milieu d’indice n0 à un milieu d’indice n. le rayon incident provenant de A va
subir une réfraction à travers le dioptre D1, l’intersection de ce rayon avec l’axe nous donne l’image A1
suivant la relation de conjugaison du dioptre sphérique :
En I’ : la lumière passe d’un milieu d’indice n à un milieu d’indice n0. le rayon réfracté en I donnant A1 va
subir une deuxième réfraction à travers le dioptre D2, l’intersection de ce rayon avec l’axe nous donne
l’image A2 suivant la relation de conjugaison du dioptre sphérique:
Dans le cas où cette lentille est mince, on aura S1≡S2≡O. d’où les équations 1 et 2 deviennent :
Sommant les deux équations nous obtenons :
Qui est la relation de conjugaison d’une lentille mince.
- La distance focale :
Par définition  est la distance focale de la lentille, comme les foyers de la lentille sont symétriques
et que   . Nous concluons que :   
Sachant également que le foyer image est la position de l’image d’un objet provenant de l’infini i.e. :
Fig. 7
C1
C2
I
I'
S2
S1
A
A'
A1
n
n0
n0
D1
D2
D2
n0
n0
n
D1