3e revisions angles

Classe de 3e – Révisions angles.
Exercice 1
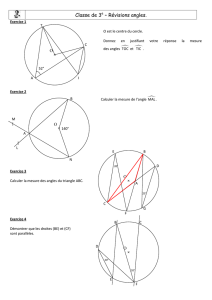
O est le centre du cercle.
Donnez en justifiant votre réponse la mesure
des angles  TOC et  TIC .
Exercice 2
Calculer la mesure de l’angle  MAL .
Exercice 3
Calculer la mesure des angles du triangle ABC.
Exercice 4
Démontrer que les droites (BE) et (CF)
sont parallèles.
B C
D
20°
20°
E
F
O
T
C
52°
A I
B
M
|
140°
A
|
L
N
O
O
E B
20° D
A
25°
C
G
F
O

Exercice 5
ABCDEFGH est un octogone régulier de centre O.
1) Calculez la mesure de l’angle  BOA . Justifiez.
2) Quelle est la nature du triangle COA ?
3) Quelle est la mesure de l’angle  BEA . Justifiez.
Exercice 6
PLYGNE est un hexagone régulier inscrit dans le cercle (C)
de centre O et de rayon 4 cm.
1) Calculez la mesure de l’angle  NOE . Justifiez.
2) Quelle est la nature du triangle NOE ?
3) Soit S le milieu de [EN].
Que représente la droite (OS) pour le triangle NOE ?
4) Calculer OS.
5) Calculer l’aire de NOE.
6) En déduire l’aire de l’hexagone PLYGNE.
7) L’hexagone PLYGNE occupe-t-il plus ou moins de 85% de l’aire du disque ?
8) Quelle est la mesure de l’angle  ELG ?
L
Y
P
O
G
E
N
O
A
B
C
D
E
F
G
H

Classe de 3e – Révisions angles – Correction
Exercice 1
O est le centre du cercle.
Donnez en justifiant votre réponse la mesure
des angles  TOC et  TIC .
TOC est l’angle au centre associé à l’angle inscrit  TAC donc
TOC = 2 ×  TAC = 2 × 52 = 104°.
TIC et  TAC sont deux angles inscrits qui interceptent le
même arc  TC donc  TIC =  TAC = 52°.
Exercice 2
Calculer la mesure de l’angle  MAL .
BAN est un angle inscrit associé à l’angle au centre  BON
donc  BAN =
BON
2 = 140 2 = 70°
BAN et  MAL sont deux angles opposés par le sommet donc
MAL = = 70°
Exercice 3
Calculer la mesure des angles du triangle ABC.
BCD et  BGD sont deux angles inscrits qui interceptent
le même arc  BD donc  BCD =  BGD = 25°.
BCA = 25°
CEF et  CBF sont deux angles inscrits qui interceptent
le même arc  CF donc  CEF =  CBF = 20°.
CBA = 20°
Dans le triangle ABC,
CAB = 180 –  BCA –  CBA = 180 – 25 – 20 = 135°
Donc :  BCA = 25°  CBA = 20°  CAB = 135°
O
T
C
104°
52°
52°
A I
B
M
|
140°
70° A 70°
|
L
N
O
O
E B
20° 20° D
135°
A
25° 25°
C
G
F

Exercice 4
Démontrer que les droites (BE) et (CF) sont parallèles.
EDF et  EBF sont deux angles inscrits qui interceptent
le même arc  EF donc  EDF =  EBF = 20°.
Les angles alternes-internes  EBF et  BFC ont la même
mesure donc les droites (BE) et (CF) sont parallèles
Exercice 5
ABCDEFGH est un octogone régulier de centre O.
1) Calculez la mesure de l’angle  BOA . Justifiez.
ABCDEFGH est un polygone régulier à 8 côtés de centre O
donc  BOA = 360
8 = 45°
2) Quelle est la nature du triangle COA ?
OC = OA (rayons) donc COA est un triangle isocèle en O.
COA =  COB +  BOA = 45 + 45 = 90° donc COA est un triangle rectangle en O.
COA est un triangle rectangle isocèle en O.
3) Quelle est la mesure de l’angle  BEA . Justifiez.
BEA est un angle inscrit associé à l’angle au centre  BOA donc  BEA =
BOA
2 = 45 2 = 22,5°
B C
20°
D
20°
20°
E
F
O
O
A
B
C
D
E
F
G
H

Exercice 6
PLYGNE est un hexagone régulier inscrit dans le cercle (C)
de centre O et de rayon 4 cm.
1) Calculez la mesure de l’angle  NOE . Justifiez.
ABCDEFGH est un polygone régulier à 6 côtés de centre O
donc  NOE = 360
6 = 60°.
2) Quelle est la nature du triangle NOE ?
OE = ON (rayons) donc NOE est un triangle isocèle en O.
NOE est un triangle isocèle qui a un angle de 60° donc NOE est un
triangle équilatéral.
3) Soit S le milieu de [EN].
Que représente la droite (OS) pour le triangle NOE ?
(OS) passe par le sommet O et par le milieu de [EN] donc (OS) est une médiane du triangle NOE.
Dans un triangle équilatéral, les médianes, les hauteurs, les médiatrices et les bissectrices sont confondues, donc (OS)
est aussi une hauteur, une médiatrice et une bissectrice pour le triangle NOE.
4) Calculer OS.
D’après le théorème de Pythagore dans le triangle ESO rectangle en S, on a :
OE² = ES² + OS²
4² = 2² + OS²
16 = 4 + OS²
OS² = 16 – 4
OS² = 12
OS = 12
OS = 4 × 3
OS = 4 × 3
OS = 2 3 cm
5) Calculer l’aire de NOE.
AireNOE = b × h
2 = NE × OS 2 = 4 × 2 3 2 = 4 3 cm²
6) En déduire l’aire de l’hexagone PLYGNE.
AirePLYGNE = 6 × AireNOE = 6 × 4 3 = 24 3 cm²
7) L’hexagone PLYGNE occupe-t-il plus ou moins de 85% de l’aire du disque ?
Aire du disque =  × r² =  × 4² = 16 cm²
AirePLYGNE
Aire du disque × 100 = 24 3
16 × 100  82,7%
PLYGNE occupe moins de 85% du disque.
8) Quelle est la mesure de l’angle  ELG ?
EOG = 60 × 2 = 120°
ELG est un angle inscrit associé à l’angle au centre  EOG donc  ELG =
EOG
2 = 120 2 = 60°
L
Y
P
O
G
E S
N