89347497-MCC-Hacheur

CRET
MOTEUR A COURANT
CONTINU et HACHEUR
SERIE
TP N° 28
1
On se propose d'étudier le fonctionnement d'un moteur à courant continu à excitation
indépendante et constante alimenté par un hacheur série à transistor MOS de
puissance.(figure1)
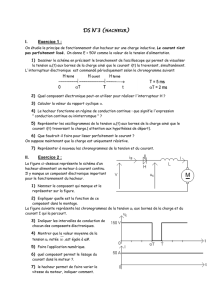
is ic
LS
iD
U= C DRL uc
Figure 1 : Ls inductance de lissage éventuelle.
1-PREPARATION
On désigne par τ la constante de temps électrique L/R (R, L : résistance et inductance de la
boucle d'induit) , par T la période de fonctionnement du hacheur et par α le rapport cyclique.
Le moteur pourra être modélisé par un dipôle actif E, R, L. (sa réaction magnétique d’induit
est négligeable)
E est sa fcem . A excitation constante, on peut poser E = Kn avec K = constante de Fcem et n,
fréquence de rotation en tr/mn.
1-1-Fonctionnement en conduction continue.
Pour un rapport cyclique α= 0.75 et une fréquence fixe 1/T = f = 100 Hz :
- Tracer, en concordance des temps, les graphes de uc(t), ic(t), is(t), id(t).
- Donner l'allure de Uc = f(Ic) ,Uc, Ic étant les valeurs moyennes de uc et ic.
- Dans le cas où τ >>T, montrer que l'ondulation ∆I= Imax - Imin du courant vaut
∆I=Uα(1-α)/f.L
Vérifier qu’elle est maximale pour α = 0,5.
Etablir qu’à la limite de la conduction continue Ic = ∆I/2.
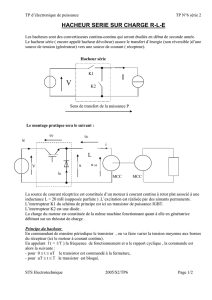
IdM
Hacheur H
M G

CRET
MOTEUR A COURANT
CONTINU et HACHEUR
SERIE
TP N° 28
2
Dans le cas où τ est de l’ordre de T, la résistance R doit être prise en compte dans les
équations de fonctionnement du moteur.
On peut montrer que l’ondulation du courant vaut :
∆I= Imax - Imin = U [1-exp(-αT/τ) + exp(-T/τ) - exp(α-1)T/τ]
R [1 - exp(-T/τ)]
Vérifier qu’elle est maximale pour α = 0,5.
1-2-Fonctionnement en conduction discontinue.
Pour un rapport cyclique faible et/ou à faible charge, le courant ic est interrompu
périodiquement.
Tracer, en concordance des temps, les graphes de uc(t), ic(t), is(t), id(t);
Dans le cas où τ>>T , montrer que la relation Ic = f(Uc) qui permet de fixer la limite entre la
conduction discontinue est l'équation d'une parabole.
1-3-Réseau de caractéristiques du moteur.
Exprimer , en fonction de α, U, R, K, Ic, la fréquence de rotation n et le moment du couple
électromagnétique Te du moteur.
Ce dernier peut se mettre sous la forme: Te = K'.Ic
Ecrire la relation liant les deux constantes K’ et K.
Montrer qu’à partir du réseau de caractéristiques Uc = f(Ic) tracé pour différentes valeurs de
α, on peut déduire le réseau de caractéristiques mécaniques Te = f( n)?
2-ETUDE EXPERIMENTALE.
Moteur utilisé: moteur CC1 U= 180V; I= 1A;
Charge : Dynamo 180V ; 1A ;
L’excitation des deux machines est maintenue constante.
La Fréquence de rotation est donnée par un alternateur tachymétrique monté en bout d’arbre
( cste : 0.016V/(tr/mn) )
La tension a l’entrée du hacheur issue d’un pont redresseur et filtrée par un condensateur
polarisé (attention au branchement !) devra être maintenue à une valeur constante U = 160V
pendant toute la manipulation.
La fréquence f = 1/T de fonctionnement du hacheur est constante et égale à 100Hz.

CRET
MOTEUR A COURANT
CONTINU et HACHEUR
SERIE
TP N° 28
3
Mesurer la résistance R et l’inductance L de l’induit
Calculer la constante électrique τ et la comparer à la période T.
2-2-Fonctionnement à f = 100 Hz .
• Régler α = 0.50 à l’oscilloscope.(points tests prévus sur la maquette).Situer, en faisant
varier la charge, la limite de conduction continue.
Relever l’ondulation ∆I du courant ic(t) et calculer le facteur de forme .
Mesurer les valeurs moyennes Uc, Ic et la vitesse n.
Relever uc(t), ic(t) à l’oscilloscope, pour un fonctionnement :
-en conduction discontinue.
-en conduction continue.
• Pour α = 0.25, 0.75, 1:
Situer la limite de conduction continue.
Mesurer Uc , Ic, n, ∆I.
Tracer les réseaux de caractéristiques Uc = f(Ic), n = f(Ic) .
2-2-Exploitation .
• En utilisant les résultats du 1-3 et les relevés:
Calculer les constantes K et K’.
Prédéterminer pour α = 0.25, 0.50, 0.75, 1 :
- Le réseau n = f(Ic).Comparer avec le réseau relevé.
- Le réseau Te = f(n) .
- Les valeurs de Ic à la limite de la conduction continue. Comparer avec les valeurs
relevées.
- Les valeurs de l’ondulation ∆I en conduction continue. Comparer avec les valeurs
relevées.
• Pour α = 0.50, et pour différentes charges, calculer le rendement du moteur, du hacheur et
de l'association hacheur-moteur.