serie-2- sciences physiques dipole RC et Cinétique

BARHOUMI MOURAD Page 1 sur 10 4M / 2020-2021
CHIMIE
On mélange à l’instant de date t=0s et à une température un volume V1= 0.1L d’une
solution (S1) d’iodure de potassium (K+ , I-) de concentration C1 avec un volume V2=0,1L
d’une solution (S2) de peroxodisulfate de sodium (2Na+ , S2O82-) de concentration C2 .La
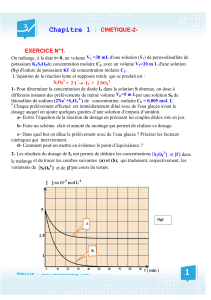
figure ci-dessous représente la variation [S2O82-]=f(t).
1) Ecrire l’équation de la réaction qui a eu lieu, en précisant les couples redox mis en jeu.
2) Déduire de la courbe la quantité de matière initiale n0(S2O82-) dans le mélange puis calculer la
concentration C2.
3) a- Dresser le tableau descriptif d’évolution du système.
b-Calculer l’avancement final xf de la réaction.
c- Déterminer la concentration molaire C1 sachant que la réaction est pratiquement totale.
BARHOUMI. Mourad
Section : 4M-4Sc.Exp
0
10
20
30
40
50
60
70
80
90
100
110
120
t(min)
2
4
6
8
10
12
14
16
18
20
[S2O82-](10-3mol.L-1)

BARHOUMI MOURAD Page 2 sur 10 4M / 2020-2021
Correction
4) Déterminer la vitesse volumique moyenne de la réaction VVmoy(t1 ;t2) entre les instants t1=10min et
t2=50min.
5) a-Définir la vitesse volumique instantané VV(t) .
b-Déterminer sa valeur à l’instant de date t3 =25min
6) A un instant de date t4, on prélève un volume V0=10mL de mélange précédent et on dose le diiode
formées à l’aide d’une solution (S) de thiosulfate du sodium (2Na+ + S2O32-) de concentration
C=2 .10-2mol.L-1 .
a-Ecrire l’équation de la réaction de dosage.
b-A l’équivalence le volume de la solution (S) ajouté est V=12mL. Déterminer la composition de
mélange à l’instant de date t4. En déduire l’instant t4.
1-
2 I-(aq) + S2O82-(aq) → I2 (aq) + 2SO42-(aq)
Couples Redox: I2 (aq) / I–(aq) ; S2O82–(aq) / SO42–(aq)
2- [ 28
2]= 28
2
+
 28
2= [ 28 2] x (+) = 20x10-3 x(0.1+0.1) = 4x10-4 mol
n(S2O82-)0 = C2 V2  C2= 28
2
 = × . = 4x10-3 mol.L-1

BARHOUMI MOURAD Page 3 sur 10 4M / 2020-2021
3- a-
Equation chimique
2 I-(aq) + S2O82-(aq) → I2 (aq) + 2 SO42-(aq)
Etat du
système
Avancement
(mol.L-1)
Concentrations molaires (mol.L-1)
Etat initial
y = 0
[  ]
[ 28
2]=20x10-3
0
0
Etat
intermé-
diaire
y
[  ] - 2 y
[ 28
2] – y
y
2 y
Etat final
Yf
[  ] - 2 yf
[ 28
2] – yf
yf
2yf
b- = 
+  xf = yf x (V1+V2)
On a
[ 28
2] = [ 28 2] – yf
 yf = ([ 28
2] – [ 28 2] )
D’après la courbe on a [ 28
2] = 5x10-3 mol.L-1
 yf = = ( 20x10-3 - 5x10-3 ) = 15 x10-3 mol.L-1
 xf= yf x (V1+V2) = 15x10-3 x (0.2) = 30x10-4 mol
c- d’après la courbe le réactif limitant est I- puisque 28
2 est le réactif en excès
car [ 28
2] > 0
 [ ] - 2yf = 0  [  ] = 2xyf =2x15 x10-3 =30 x10-3 mol.L-1

BARHOUMI MOURAD Page 4 sur 10 4M / 2020-2021
 = [  ] x (+) =30x10-3 x(0.1+0.1) = 60x10-4 mol
  = C1 V1  C1= 
 = × . = 60x10-3 mol.L-1
4- VVmoy(t1 ;t2) = - [ 28
2]  [ 28 2]
 = -     x10-3= 2x10-4 mol.L-1.min-1
5 – a - VV(t)= 
 v(t) =   = (
)
 = 
b- VV(t3)= 
)t3= - [ 28
2]
 )t3= - (pente de la tangente à la courbe à t3)
= -   
 x10-3 =2x10-4 mol.L-1.min-1
6- a-
L’équation de la réaction de dosage.
I2 (aq) + 2 S2O32-(aq) → 2 I-(aq) + S4O62-(aq)
b- à l’équivalence on a
= 23
2
  [ ] x V0= 
 [ ] = 
 =    = 12 x10-3 mol.L-1
D’ou la composition du mélange à l’instant t4
[ ] = 12 x10-3 mol.L-1 = y
[  ] = [  ] - 2 y = 30 x10-3 – 2x12 x10-3 = 6 x10-3 mol.L-1
[ 4
2] = 2 y = 2x 12 x10-3 = 24 x10-3 mol.L-1
[ 28
2] = [ 28 2] – y = 20 x10-3 - 12 x10-3 = 8 x10-3 mol.L-1
D’après la courbe pour [ 28
2] = 8 x10-3 mol.L-1 on a t4=30 min

BARHOUMI MOURAD Page 5 sur 10 4M / 2020-2021
PHYSIQUE
Partie A
On réalise un circuit électrique, comportant en série, un générateur idéal de courant débitant un courant
d’intensité constante Io=50µA, un conducteur ohmique, un interrupteur K, un condensateur de capacité
C inconnue et un voltmètre.
A un instant pris comme origine des temps (t=0), on ferme l’interrupteur K et on suit l’évolution de la
tension uc aux bornes du condensateur au cours du temps, ce qui a permis de tracer la courbe d’évolution
de l’énergie électrique Ec emmagasinée dans le condensateur en fonction du carré du temps.(figure 3)
1- Représenter le schéma du montage qui permet de suivre l’évolution de la tension uc au cours
du temps.
2- En exploitant le graphe, déterminer la capacité C du condensateur.
3- Le condensateur utilisé est plan de permittivité électrique absolue ε, l’aire de la surface
commune en regard est s=1m2 et l’épaisseur du diélectrique est e=0,01mm. Calculer la
permittivité relative du condensateur.
On donne ε0=8,85.10-12 usi.
Partie B
On se propose de déterminer la capacité C par une autre méthode pour cela on réalise un
circuit électrique en série comportant un générateur de tension idéal de f.é.m. E , deux
résistors dont l’un est de résistance R1 =150  et R2 inconnue, un condensateur de
capacité C initialement déchargé et un interrupteur K ( figure-3 )