Quadrilatères. - Maths au LFKL

I. Définition :
II. Parallélogrammes :
a) Définition.
Exemple : ABCD est un parallélogramme, son centre de symétrie est le point O.
b) Propriétés du parallélogramme.
Si les sommets opposés sont symétriques, alors on peut prouver que …
c) Critère de reconnaissance d’un parallélogramme.
Attention : Un quadrilatère qui a deux côtés parallèles n’est pas forcement un parallélogramme.
C’est le cas du trapèze.
Avoir deux côtés parallèles est une condition ………. mais pas …………… pour pouvoir affirmer
qu’un quadrilatère est un parallélogramme.
Un quadrilatère qui a seulement deux côtés de même longueur n’est pas forcement un parallélogramme.
Quadrilatères.
Un quadrilatère est un polygone qui a quatre côtés.
Définition
A
B
D
C
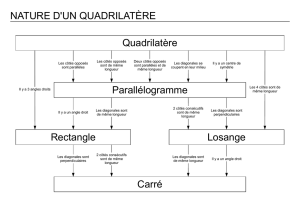
Dans un parallélogramme, on peut affirmer que :
- Les diagonales ont le même milieu.
- Les côtés opposés sont parallèles.
- Les côtés opposés sont de même longueur.
- Les angles opposés sont de même mesure.
Propriétés
Un parallélogramme est un quadrilatère qui a un centre de symétrie.
O
Définition
A
B
D
C
Si un quadrilatère a ses diagonales qui ont le même milieu, alors on peut affirmer que c’est un parallélogramme.
Si un quadrilatère a ses côtés opposés parallèles deux à deux, alors on peut affirmer que c’est un parallélogramme.
Si un quadrilatère a tous ses côtés opposés de même longueur, alors on peut affirmer que c’est un parallélogramme.
Si un quadrilatère a deux côtés opposés parallèles et de même longueur, alors on peut affirmer que c’est un
parallélogramme.
Propriétés
A
D
C
B
69

III. Parallélogrammes particuliers :
a) Le losange.
Un losange a ses quatre côtés de même longueur, donc en particulier, il a ses côtés opposés de même longueur, donc c’est
un parallélogramme. Donc : Un losange est un parallélogramme donc il possède toutes les propriétés d’un
parallélogramme : Un losange à un centre de symétrie, il a ses diagonales qui ont le même milieu, il a ses côtés opposés
parallèles, il a ses angles opposés de même mesure.
C’est un parallélogramme particulier car il possède en plus deux propriétés :
 Ses quatre côtés sont de même longueur.
 Ses diagonales sont perpendiculaires.
b) Le rectangle.
Un rectangle a ses côtés opposés parallèles, donc c’est un parallélogramme. Donc : Un rectangle est un
parallélogramme donc il possède toutes les propriétés d’un parallélogramme : Un rectangle à un centre de symétrie, il a
ses diagonales qui ont le même milieu, il a ses côtés opposés parallèles, il a ses angles opposés de même mesure.
C’est un parallélogramme particulier car il possède en plus deux propriétés :
 Ses quatre angles sont droits. (deux côtés consécutifs sont perpendiculaires.)
 Ses diagonales sont de même longueur.
b) Le carré.
Remarque : Un carré est un parallélogramme donc il possède toutes les propriétés d’un parallélogramme :
Un carré à un centre de symétrie, il a ses diagonales qui ont le même milieu, il a ses côtés opposés parallèles, il a ses
angles opposés de même mesure. Un carré est un losange ( il a ses quatre côtés de même longueur ) donc il a en plus les
propriétés propres aux losanges: ses diagonales sont perpendiculaires. Un carré est un rectangle ( il a ses quatre angles
droits ) donc il a en plus les propriétés propres aux rectangles : ses diagonales sont de même longueur.
Un losange est un quadrilatère qui a ses
quatre côtés de même longueur.
Définition
M
N
O
P
Si un parallélogramme a deux côtés consécutifs de même
longueur alors on peut affirmer que c’est un losange.
Propriété
Un rectangle est un quadrilatère qui a quatre
angles droits.
Définition
I
J
K
L
Si un parallélogramme a ses diagonales perpendiculaires
alors on peut affirmer que c’est un losange.
Propriété
Si un parallélogramme a un angle droit alors on peut
affirmer que c’est un rectangle.
Propriété
Un carré est un quadrilatère qui a ses quatre côtés de même
longueur et quatre angles droits.
………………………………………………..
Définition
R
S
T
Q
Si un parallélogramme a ses diagonales de même
longueur alors on peut affirmer que c’est un rectangle.
Propriété
70

IV. Familles de quadrilatères :
71