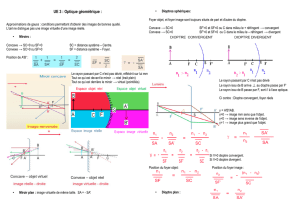
Optique Géométrique : Profondeur Apparente et Interfaces Courbes
Telechargé par
aide windev
Ch # 5:
Cours #7: Optique Géométrique (II)
Zéhira.Hamoudi, PhD
1
2
Objectifs
Profondeur Apparente
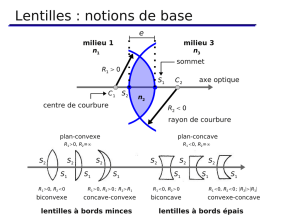
Interfaces Courbes
i. Lentille épaisses;
ii. Lentilles minces;
iii. Miroirs sphériques
Nous intéressons aux:
Systèmes Optiques
3
•Un système optique est une combinaison d’un ou plusieurs types d’interfaces
•Son rôle: est de produire une image à partir d’un objet.
•Un objet est le lieu de concours des faisceaux
incidents et il est deux types:
-Réel: s’il est du coté incident (devant le système
optique) en émettant des rayons divergent
- Vitruel: si il n’est pas du coté incident
(prolongement si nécessaire)
•Une image est le lieu de concours des faisceaux
émergents (prolongement si nécessaire)
Systèmes Optiques
4
Illustration: objet réel, virtuel, image réelle et virtuelle
Production d’une image réelle à
partir d’un objet réel
Production d’une image réelle à
partir d’un objet virtuel
Objet de l’autre
coté de système
optique
Objet est du
coté incident
objet
image
Axe optique
Systèmes Optiques
5
Illustration: objet réel, virtuel, image réelle et virtuelle
Production d’une image virtuelle à
partir d’un objet réel
Production d’une image virtuelle
à partir d’un objet virtuel
Objet de l’autre
coté de système
optique
Objet est du
coté incident
objet
image
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
1
/
50
100%
