2014-02-04 22-38-01 Module1 Algebra Review

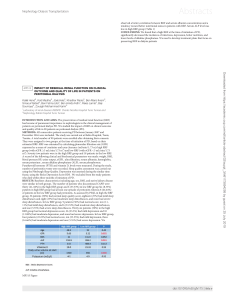
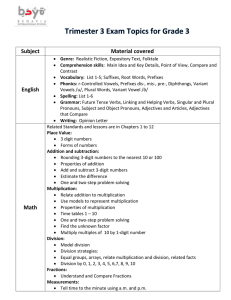
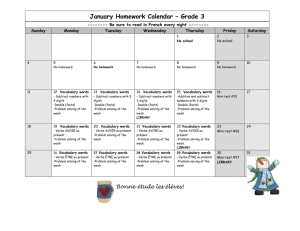
Surviving Introduction to
Finance
Module 1 –Algebra Review

Topics for discussion
Order of operations
Combining like terms
Distributive property
Solving for a variable

Order of operations
As expressions and equations may have parentheses,
exponents, and other math operations, there exists a
means to consistently simplify them.
Think of order of operations as directions for simplifying
expressions and equations.
Use the acronym PEMDAS
1) Parentheses
2) Exponents
3) Multiplication and division, from left to right
4) Addition and subtraction, from left to right

Order of operations
Examples
11-5-2
First, look for parentheses, then exponents,
followed by multiplication and division. As
there are none of these, next move to
addition and subtraction, left to right
11-5 = 6 First complete 11-5
6-2 = 4 Put 6 back into expression and again
move from left to right

Order of operations
Examples
5 + 12/3
First step is division (recall a fraction is
nothing more than division).
12/3 is 4
All that is left is addition
5 + 4
9