Thèse Bouchebbat

REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE
UNIVERSITE DU 20 AOUT 1955 SKIKDA
Faculté de Technologie
Département : Génie Electrique
Thèse
diplôme de :
Doctorat LMD
Spécialité : AUTOMATIQUE
Thème
Algorithmes bio-inspirés appliqués pour la commande
des systèmes
Par : Rochdi BOUCHEBBAT
Soutenu Le : 21/05/2017 Devant Le Jury:
Président LACHOURI Abderrazek Pr Université de Skikda
Rapporteur GHERBI Sofiane MCA Université de Skikda
Examinateur BOUDEN Toufik Pr Université de Jijel
RAMDANI Messaoud Pr Université de Annaba
AHMIDA Zahir MCA Université de Skikda
MEHENAOUI Lamine MCA Université de Skikda
Code : D012117005D

À ma famille

Remerciements
Je remercie ALLAH le tout puissant pour la volonté et la patience qu'il m'a donné tout au
long de mes études.
Je tiens à remercier particulièrement Monsieur Sofiane GHERBI, Maître de conférence à
l'université de Skikda pour la proposition du sujet de cette thèse et pour son soutien tout au
long de ce travail. Merci Monsieur pour vos conseils et la confiance que vous m'avez accordé
au cours de ces années d'encadrement.
Je tiens à remercier chaleureusement, Monsieur Abderazek LACHOURI, Professeur à
l'université de Skikda, d'avoir accepté la présidence du jury de ma soutenance, ainsi que
Messieurs Toufik BOUDEN, Professeur à l'université de Jijel, Messaoud RAMDANI,
Professeur à l'université de Annaba, Lamine MEHENNAOUI Maître de conférence à
l'université de Skikda et Zahir AHMIDA Maître de conférence à l'université de Skikda, qui
ont accepté d'examiner mon manuscrit de thèse.
a offert tout au long de mon Doctorat.
J'adresse un grand merci à mes amis et collègues Abderahmane GANOUCHE, Adel
MAKHBOUCHE, et à tous ceux qui m'ont aidé de près ou de loin durant ces années de
recherche et d'études.
À tous mes enseignants tout le long de ma formation à l'université de Skikda.
R. Bouchebbat …

Résumé - 
n effet, la nature trouve toujours des solutions optimales pour sa survie. Dans
-
inspirés dans tous les domaines. Dans cette thèse, on fait une synthèse des différents
algorithmes bio-inspirés récents, et leur potentielle exploitation dans le domaine de
contribution non
négligeable sots à la commande des systèmes soit      
inspiré du système immunitaire peut augmenter de façon substantielle la robu 
boucle de commande. Les réseaux de neurones inspirés du fonctionnement du cerveau
sont trouvée        
les essaims particulaires ou parles colonies de fourmis.  de
ces algorithmes bio-inspirés pour la commande de systèmes particuliers, soumis à diverses
contraintes, montre un apport certain.
Mots-clés - systèmes bio-inspirés, optimisation, commande des systèmes.
Abstract - The observation of natural phenomena has always been a source of inspiration for
the human being; in fact, nature always finds optimal solutions for its survival. In this context,
there has recently been a strong trend towards the use of bio-inspired systems in all fields. In
this thesis, we synthesize the various recent bio-inspired algorithms, and their potential use in
the field of automation. Each of these algorithms, according to its specificity, makes a
significant contribution to the control of systems and to optimization. Indeed, a controller
inspired by the immune system can substantially increase the robustness of a control loop,
neural networks inspired by the functioning of the human brain; bring their adaptability and
their ability to learn. Optimal solutions can be found by bio-inspired optimization algorithms
such as genetic algorithm, optimization by particulate swarms or ant colonies. The application
of these bio-inspired algorithms for the control of particular systems, subjected to various
constraints, shows a certain contribution.
Keywords - Bio-inspired systems, optimization, control systems.

iv
Table des matières
Introduction générale 1
I Généralités sur les systèmes bio-inspirés ............................................................................. 6
I.1 Introduction ...................................................................................................................... 6
I.2 Systèmes bio-inspirés pour la commande ......................................................................... 7
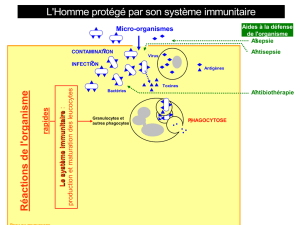
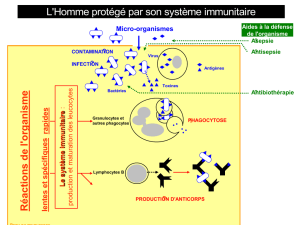
I.2.1 Le système immunitaire artificiel .............................................................................. 7
I.2.1.1 Le système immunitaire biologique .................................................................... 8
I.2.1.2 Principales caractéristiques ................................................................................ 10
I.2.1.3 Principales théories immunitaires ...................................................................... 10
I.2.1.4 Les algorithmes immunitaires artificiels ............................................................ 11
I.2.2 Le système neuronal artificiel .................................................................................. 14
I.2.2.1 Le neurone biologique ...................................................................................... 14
I.2.2.2 Le neurone artificiel .......................................................................................... 15
 ........................................ 17
I.2.2.4 Architecture du réseau neuronal artificiel ......................................................... 18
-inspirés ......................................................................... 21
I.3.1 Les algorithmes évolutionnaires .............................................................................. 21
I.3.1.1  ..................................................................................... 22
I.3.1.2 La programmation génétique ............................................................................ 23
I.3.1.3 La programmation évolutionnaire ..................................................................... 25
 .................................................. 26
 ..................................... 27
 ........................................ 35
I.4 Conclusion ...................................................................................................................... 38
II Conception d’une loi de commande robuste inspirée par le système immunitaire ...... 39
II.1 Introduction .................................................................................................................... 39
II.2 La commande robuste .................................................................................................... 39
 ............. 41
II.3.1 Mécanisme de la rétroaction immunitaire ............................................................... 41
II.3.2 Modélisation de la loi de rétroaction immunitaire .................................................. 42