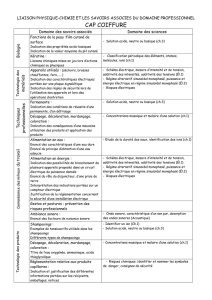
Lois de Kirchhoff en régime sinusoïdal - Cours d'électrotechnique

École Nationale Polytechnique d’Alger Électrotechnique générale
CHAPITRE I
LES LOIS DE KIRSHHOFF EN RÉGIME
SINUSOÏDAL
Le courant alternatif est largement utilisé dans divers domaines de l’électrotechnique. Presque
dans tous les cas, l’énergie électrique est produite, distribuée et consommée sous forme d’énergie à
courant sinusoïdal.
Même si à l’heure actuelle les progrès réalisés en électronique de puissance permettent de plus en
plus l’utilisation du transport en courant continu, l’énergie est distribuée principalement sous
forme de courant alternatif.
Ceci s’explique par le fait que le courant alternatif permet très facilement la transformation d’une
tension élevée en une basse tension et inversement (voir transformateurs). Ce procédé de
transformation est en effet indispensable pour le transport de l’énergie à partir de la centrale
jusqu’au consommateur.
Ce chapitre a donc pour objectif de rappeler certaines notions élémentaires traitant des circuits
simples à courant alternatif (monophasés).
Rappelons que les lois de Kirchhoff (loi des mailles & loi des nœuds) sont les lois fondamentales
qui régissent le fonctionnement de tout circuit électrique. Appliquées aux circuits à courant
continu, elles offrent la possibilité de calculer les différences de potentiel et courants, même dans
les circuits les plus complexes.
Elles demeurent valables en régime sinusoïdal à chaque instant et il est donc possible d’écrire les
équations en valeurs instantanées et de résoudre les différents problèmes d’électrocinétique en
tenant compte des régimes transitoires.
Cependant, si seul le régime permanent nous intéresse, on peut simplifier les équations en
introduisant le concept de vecteur tournant, puis de valeur complexe équivalente. Les équations
en sont grandement simplifiées et répondent parfaitement à notre besoin.
On applique alors les lois de Kirchhoff de la même façon que pour un circuit continu, en
introduisant la notion d’impédance complexe, qui impose le déphasage entre courant–tension et
dont il faut tenir compte dans chaque branche d’un circuit.
En résumé, ce chapitre a pour objectif de familiariser l’étudiant avec la notation complexe
indispensable à la résolution des calculs des réseaux monophasés
I- Introduction
Avant d’aborder le régime sinusoïdal, rappelons certaines règles de base à propos
des circuits électriques. Dans le domaine du courant continu, on a le plus souvent
affaire à des sources continues (batteries) qui délivrent une tension constante et les
récepteurs sont généralement constitués de résistances.
Toutefois, dans le domaine du courant variable (et sinusoïdal en particulier), on peut
aussi avoir affaire, en plus des résistances, à des condensateurs et des bobines qui ne
sont capables de produire un effet électrique que si, justement, le régime est variable.
Chapitre1 Le régime sinusoïdal monophasé Mme Dalila Sator-Namane 1

École Nationale Polytechnique d’Alger Électrotechnique générale
1) Règles de fléchage en régime continu
Dans le domaine du régime continu, le courant dans le schéma d'un circuit électrique
est représenté par une flèche. Mais le sens de déplacement effectif des électrons est
l'opposé du sens positif du courant :
Remarque : si après calcul dans une branche quelconque, on trouve un signe négatif
de la valeur de I, cela signifie que le sens réel du courant est inversé par rapport à
celui choisi arbitrairement au départ.
De même, on représente une tension par une flèche à proximité de l’élément
considéré, comme sur les schémas suivants (on remarque dans le cas (1) que les
flèches courant-tension sont dans le sens inverse: il s’agit de la convention récepteur,
à l’inverse du cas (2) où on parle de convention générateur) :
(1) convention récepteur (2) convention générateur
(Par exemple une résistance) (Par exemple une batterie d’accumulateur)
En général, on oriente la « flèche » vers le potentiel le plus élevé (par exemple, pour
une batterie la flèche est orientée vers la borne +) mais si on ignore les valeurs des
potentiels, on donne un sens arbitraire à la ddp et si trouve après calcul
que cela signifie que le sens de la ddp est inversé.
AB
VV0
Remarque : les éléments comportant une entrée et une sortie (A et B dans nos
exemples sont appelés dipôles électriques.
2) Les lois de Kirchhoff
 Loi des nœuds
Un nœud est un point de jonction de plusieurs conducteurs. Une des lois de
Kirchhoff, appelée loi des nœuds stipule que :
« La somme des intensités des courants arrivant à un nœud est égale à la somme des
intensités des courants sortant du nœud. »
En d’autres termes on peut aussi exprimer la loi des nœuds de la façon qui suit :
« La somme algébrique des courants arrivant à un nœud est constamment nulle. »
n
k
k1
I0
Chapitre1 Le régime sinusoïdal monophasé Mme Dalila Sator-Namane 2

École Nationale Polytechnique d’Alger Électrotechnique générale
Exemple :
On a dans ce cas :
1234
IIII 0
(ça prouve que forcément au moins un des courant est
négatif).
 Loi des mailles
Une maille est un ensemble de conducteurs et de composants électriques, partant
d'un point, et arrivant à ce même point. La loi des mailles stipule que la somme
algébrique des tensions le long de la maille est constamment nulle :
n
k
k1
V0
On choisit alors un sens arbitraire de parcours sur la maille et on exprime toutes les
tensions en fonction de ce choix. Exemple :
On a dans ce cas :
1234
VVVV 0
3) Comportement des dipôles électriques usuels en régime variable
Remarque importante
Les fléchages sur les dipôles se font de la même façon que pour le régime continu (flèches courant-
tension dans le même sens pour un générateur, et dans le sens contraire pour un récepteur).
 La résistance
La résistance a la propriété d’avoir une réponse en courant i(t)
proportionnelle à la tension appliquée v(t) à tout instant. Il
s’agit de la loi d’Ohm établie en régime continu et qui peut être
étendue au régime variable. On a donc :
v(t) R i(t)
La bobine (ou inductance)
D’après la loi de Lenz, l’inductance (notée L) a la propriété de
produire à ses bornes une tension proportionnelle à la dérivée
du courant. D’une manière générale, la relation entre le courant
et la tension est donnée par :
Chapitre1 Le régime sinusoïdal monophasé Mme Dalila Sator-Namane 3

École Nationale Polytechnique d’Alger Électrotechnique générale
en général nul sauf
dans certains cas
d(Li(t)) d i(t) d L
v(t) L i(t)
dt dt dt
Dans la plupart des cas (si L=const), la loi de Lenz se résume à:
d i(t)
v(t) L dt
Remarque
D’après la relation obtenue, on note que si le courant est brutalement coupé par exemple
(discontinuité du courant dans un temps très court), on aura :
0
0
di(t)
v(t) L v(t)
dt
Cela correspondrait en théorie à une tension infinie. Mais cela signifie que pratiquement,
une ouverture brutale d’un circuit inductif conduit à une surtension transitoire qui se
manifeste par des étincelles plus ou moins dangereuses selon la puissance de la bobine
considérée.
On dit que l’inductance ne supporte pas les coupures brutales du courant qui la traverse.
Par ailleurs, en régime continu, la bobine se comporte comme un circuit fermé :
d
v(t) L 0
dt
i(t)
interrupteur fermé
 La capacité
La relation entre la valeur instantanée du courant i(t) et la
valeur de la capacité dans un tel circuit est donné par :
dq dv(t)
i(t) C
dt dt
Ainsi, la capacité est l’élément opposé de l’inductance : il
suffit d’échanger les rôles de la tension et du courant. La
capacité C correspond à une proportionnalité entre le
courant et la dérivée de la tension.
Remarque
D’après la relation obtenue, on note que si la tension varie de façon brutale, par exemple
(discontinuité de la tension dans un temps très court), on aura :
0
0
dv(t)
i(t) C i(t)
dt
Cela correspondrait en théorie à un courant infini. Mais cela signifie que pratiquement, un
changement brutal de la tension d’un circuit capacitif conduit à une surintensité ou pic
de courant.
Par ailleurs, en régime continu, la capacité se comporte comme un circuit ouvert.
Chapitre1 Le régime sinusoïdal monophasé Mme Dalila Sator-Namane 4

École Nationale Polytechnique d’Alger Électrotechnique générale
dv(t)
i(t) C 0
dt
interrupteur ouvert
II-Représentation des grandeurs sinusoïdales : de la sinusoïde au nombre complexe
Le régime sinusoïdal est un des régimes le plus usité dans le domaine de
l’électrotechnique. Aussi, et afin de se ramener à une exploitation plus simple des
équations électriques associées, des méthodes sont élaborées de façon à établir des
équations similaires à ceux utilisées en régime continu.
Les mêmes règles sont maintenues, mis à part le fait qu’elles sont applicables à chaque
instant.
Symboles conventionnels
Les valeurs instantanées sont représentées par une lettre minuscule, les valeurs efficaces par une
lettres majuscule et les valeurs maximales par une lettre majuscule avec pour indice la lettre ‘m’.
1) Représentation instantanée des grandeurs sinusoïdales
Il s’agit d’exprimer la grandeur sinusoïdale sous sa forme analytique temporelle.
Soit une grandeur sinusoïdale g(t) de pulsation ( 2f , f étant la fréquence de g(t))
qui s’exprime comme suit :
m
g(t) G sin( t ) 2Gsin( t ) 
g étant la valeur instantanée, Gm la valeur maximale, 
le déphasage par rapport à une origine choisie et G la
valeur efficace de la grandeur considérée. Si on veut
représenter la caractéristique g en fonction du temps,
elle possède l’allure ci-contre.
Notons que la valeur maximale Gm et la valeur efficace
G sont liées par la relation générale suivante:
T
22
m
0
1
GGsin(t
T
)dt
Dans le domaine électrique, la valeur efficace d’une tension alternative est égale à la
valeur d’une tension continue qui produirait le même échauffement dans une même
résistance. Dans le cas particulier du régime sinusoïdal, on trouve, naturellement:
m
G2G
2) Représentation de Fresnel ou vectorielle
Dans les circuits à courant alternatif, les tensions et courants évoluent avec le temps de
façon périodique. Selon la nature du circuit considéré (résistif, capacitif ou selfique), les
courants et tensions présentent des déphasages distincts par rapport à une origine
donnée. Aussi, la résolution analytique des équations électriques donnent souvent lieu à
des calculs plus ou moins fastidieux.
Néanmoins, si on ne tient compte que du régime permanent, il est possible de
représenter la sinusoïde par un vecteur tournant, puis aboutir à une représentation
Chapitre1 Le régime sinusoïdal monophasé Mme Dalila Sator-Namane 5